Cho 2 đường thẳng xx' và yy' song song với nhau, một đường thẳng cắt xx' và yy' lần lượt tại các điểm A, A'. Kẻ tia phân giác Az của \[\widehat {x'AA'}\] và tia phân giác A't của \[\widehat {yA'A}\]. Tia Az cắt yy' tại điểm B' và A't cắt xx' tại điểm B.
a) Chứng tỏ Az // A't.
b) Chứng tỏ \[\widehat {ABA'} = \widehat {AB'A'}\].
Quảng cáo
1 câu trả lời 45
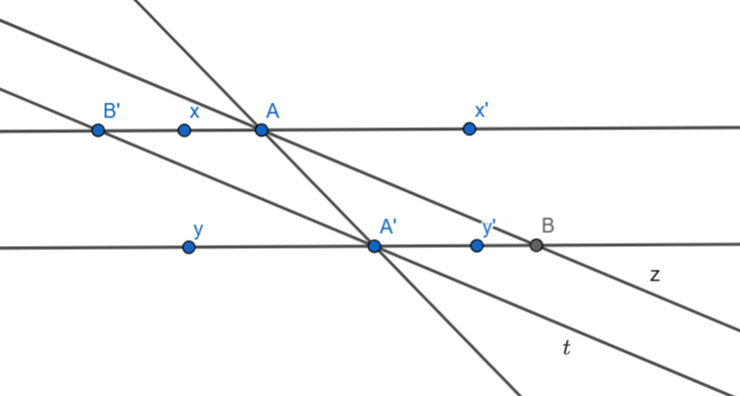
a) Xét DB'AA' và DAA'B có:
AA' là cạnh chung
\[\widehat {B'{\rm{AA}}'} = \widehat {AA'B}\] (gt)
B'A = A'B (gt)
Do đó DB'AA' = DAA'B (c.g.c)
Suy ra \[\widehat {B'A'A} = \widehat {BAA'}\] (hai góc tương ứng)
Do đó Az // A't (đpcm)
b) Ta có DB'AA' = DAA'B (cmt)
Suy ra \[\widehat {AB'A'} = \widehat {ABA'}\](đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129662
Đã trả lời bởi chuyên gia
129662 -
 Đã trả lời bởi chuyên gia
104103
Đã trả lời bởi chuyên gia
104103 -
 Đã trả lời bởi chuyên gia
94073
Đã trả lời bởi chuyên gia
94073 -
 Đã trả lời bởi chuyên gia
69393
Đã trả lời bởi chuyên gia
69393



