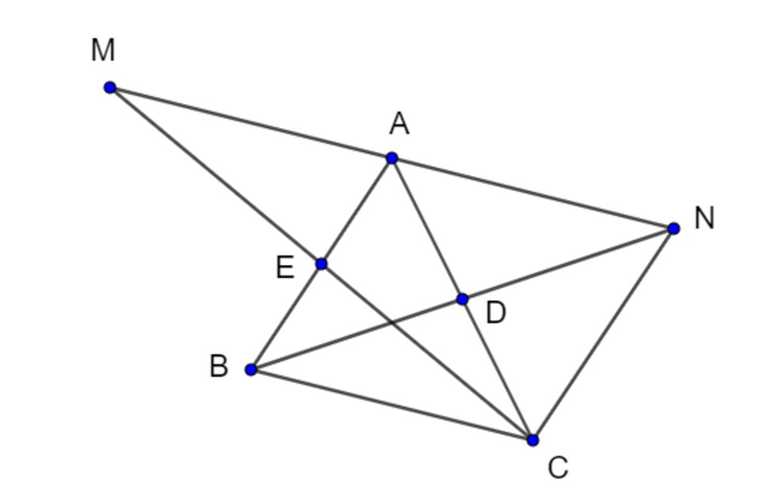
a) Xét DCDN và DADB có:

DC = DA (D là trung điểm AC)

DN = DB (gt)

\[\widehat {CDN} = \widehat {ADB}\](2 góc đối đỉnh)

Do đó DCDN = DADB (c.g.c)

b) Xét DAME và DBCE có:

ME = EC (gt)

EA = EB (E là trung điểm AB)

\[\widehat {AEM} = \widehat {BEC}\](2 góc đối đỉnh)

Do đó DAME = DBCE (c.g.c)

Suy ra \[\widehat {AME} = \widehat {BCE}\] (hai góc tương ứng)

Mà hai góc này ở vị trí so le trong của AM và BC.

Do đó AM // BC.

c) Xét DADN và DCDB có:

DN = DB (gt)

AD = DC (D là trung điểm AC)

\[\widehat {ADN} = \widehat {CDB}\](2 góc đối đỉnh)

Do đó DADN = DCDB (c.g.c)

Suy ra \[\widehat {DNA} = \widehat {DBC}\] (hai góc tương ứng)

Mà hai góc này ở vị trí so le trong của AN và BC.

Do đó AN // BC.

Lại có AM // BC (cmt) nên A, M, N thẳng hàng.

• Vì DAME = DBCE (cmt) nên AM = BC (hai cạnh tương ứng)

• Vì DADN = DCDB (cmt) nên AN = BC (hai cạnh tương ứng)

Do đó AM = AN hay A là trung điểm của MN.

Vậy A là trung điểm của MN.