Cho nửa đường tròn tâm O đường kính AB. Trên nửa đường trong lấy hai điểm C và D sao cho cung AC bé hơn cung AD (D khác B). Hai dây AD và BC cắt nhau tại M. Vẽ MN vuông góc với AB tại N.
a) Chứng minh tứ giác ACMN nội tiếp.
b) Chứng minh: AM.AD = AN.AB.
Quảng cáo
1 câu trả lời 110
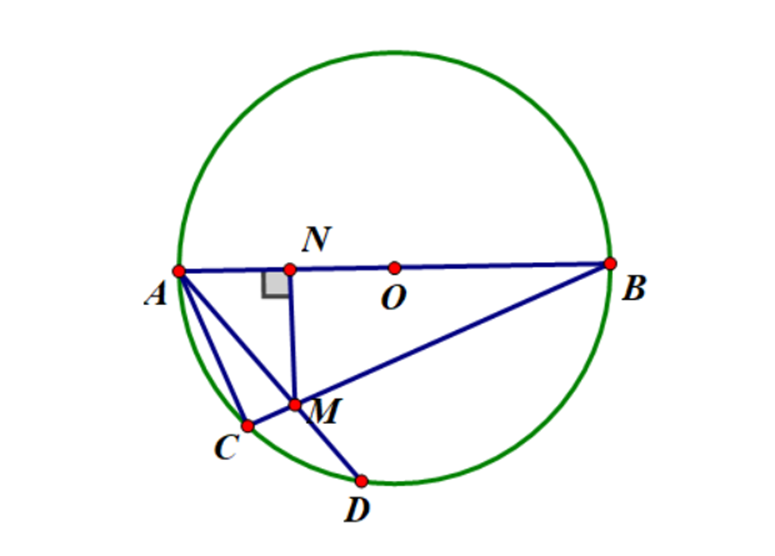
a) Ta có: MN ^ AB (giả thiết đề bài)
Và \[\widehat {ANM} + \widehat {ACM} = 180^\circ \]
Do đó tứ giác ACMN nội tiếp.
b) Xét DANM vuông tại N và DADB vuông tại D có:
\[\left\{ \begin{array}{l}\widehat {NAM}\,\,\,chung\\\widehat {ANM} = \widehat {ADB} = 90^\circ \end{array} \right.\]
Þ DANM ᔕ DADB (g.g)
\[ \Rightarrow \frac{{AN}}{{AD}} = \frac{{AM}}{{AB}}\]
Þ AM.AD = AN.AB (đpcm)
Vậy AM.AD = AN.AB.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129662
Đã trả lời bởi chuyên gia
129662 -
 Đã trả lời bởi chuyên gia
104103
Đã trả lời bởi chuyên gia
104103 -
 Đã trả lời bởi chuyên gia
94073
Đã trả lời bởi chuyên gia
94073 -
 Đã trả lời bởi chuyên gia
69393
Đã trả lời bởi chuyên gia
69393



