Cho tam giác ABC cân tại A. Trên tia đối của tía AC lấy điểm D. Trên tia đối của tia AB lấy điểm E sao cho AD = AE. Chứng minh DECB là hình thang cân.
Quảng cáo
1 câu trả lời 117
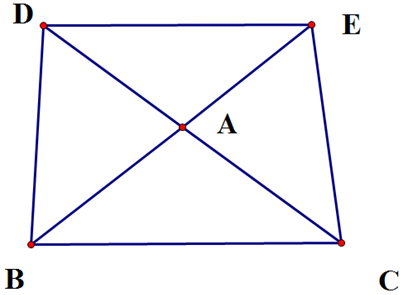
Tam giác ABC cân tại A Þ \(\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ - \widehat {BAC}}}{2}\)
Lại có AD = AE nên tam giác ADE cân tại A
\( \Rightarrow \widehat {ADE} = \widehat {AED} = \frac{{180^\circ - \widehat {DAE}}}{2}\)
Mà \(\widehat {BAC} = \widehat {DAE} \Rightarrow \widehat {ACB} = \widehat {ADE}\).
Mà 2 góc này ở vị trí so le trong nên suy ra BC // DE
Suy ra tứ giác DECB là hình thang
Xét ∆ADB và ∆AEC có:
AD = AE (gt)
AB = AC (gt)
\(\widehat {DAB} = \widehat {EAC}\) (hai góc đối đỉnh)
Þ ∆ADB = ∆AEC (c.g.c)
Þ \[\widehat {DBA} = \widehat {ECA}\] (hai góc tương ứng)
Mà \(\widehat {ABC} = \widehat {ACB}\) nên suy ra \(\widehat {DBA} + \widehat {ABC} = \widehat {ECA} + \widehat {ACB}\)
Hay \(\widehat {DBC} = \widehat {ECB}\)
Vậy tứ giác DECB là hình thang cân.
Quảng cáo
Bạn muốn hỏi bài tập?



