Quảng cáo
1 câu trả lời 93
Lời giải
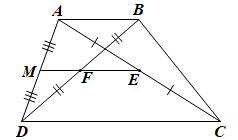
* Chứng minh EF // AB // CD.
Gọi M là trung điểm của AD.
Xét tam giác ABD có: M, F lần lượt là trung điểm của AD, BD nên MF là đường trung bình của tam giác
Suy ra MF // AB và \(MF = \frac{1}{2}AB\).
Tương tự ta cũng có ME là đường trung bình của tam giác ADC
Suy ra ME // DC và \(ME = \frac{1}{2}CD\).
Mà AB // CD nên ME // AB và MF // AB.
Qua điểm M có hai đường thẳng ME, MF cùng song song với AB nên theo tiên đề Euclid, hai đường thẳng này trùng nhau.
Hay M, E, F thẳng hàng nên EF // AB // CD.
* Chứng minh \(EF = \frac{{CD - AB}}{2}\).
Ta có: EF = ME – MF = \(\frac{1}{2}CD - \frac{1}{2}AB = \frac{{CD - AB}}{2}\).
Vậy \(EF = \frac{{CD - AB}}{2}\).
Quảng cáo
Bạn muốn hỏi bài tập?



