Quảng cáo
1 câu trả lời 197
Lời giải
a) dm: y = (2m – 1)x + 2 \(\left( {m \ne \frac{1}{2}} \right)\).
Với m = 1, ta có: y = x + 2.
Bảng giá trị của dm khi m = 1:
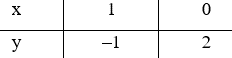
Do đó đồ thị hàm số y = x + 2 là đường thẳng đi qua hai điểm (1; –1) và (0; 2).
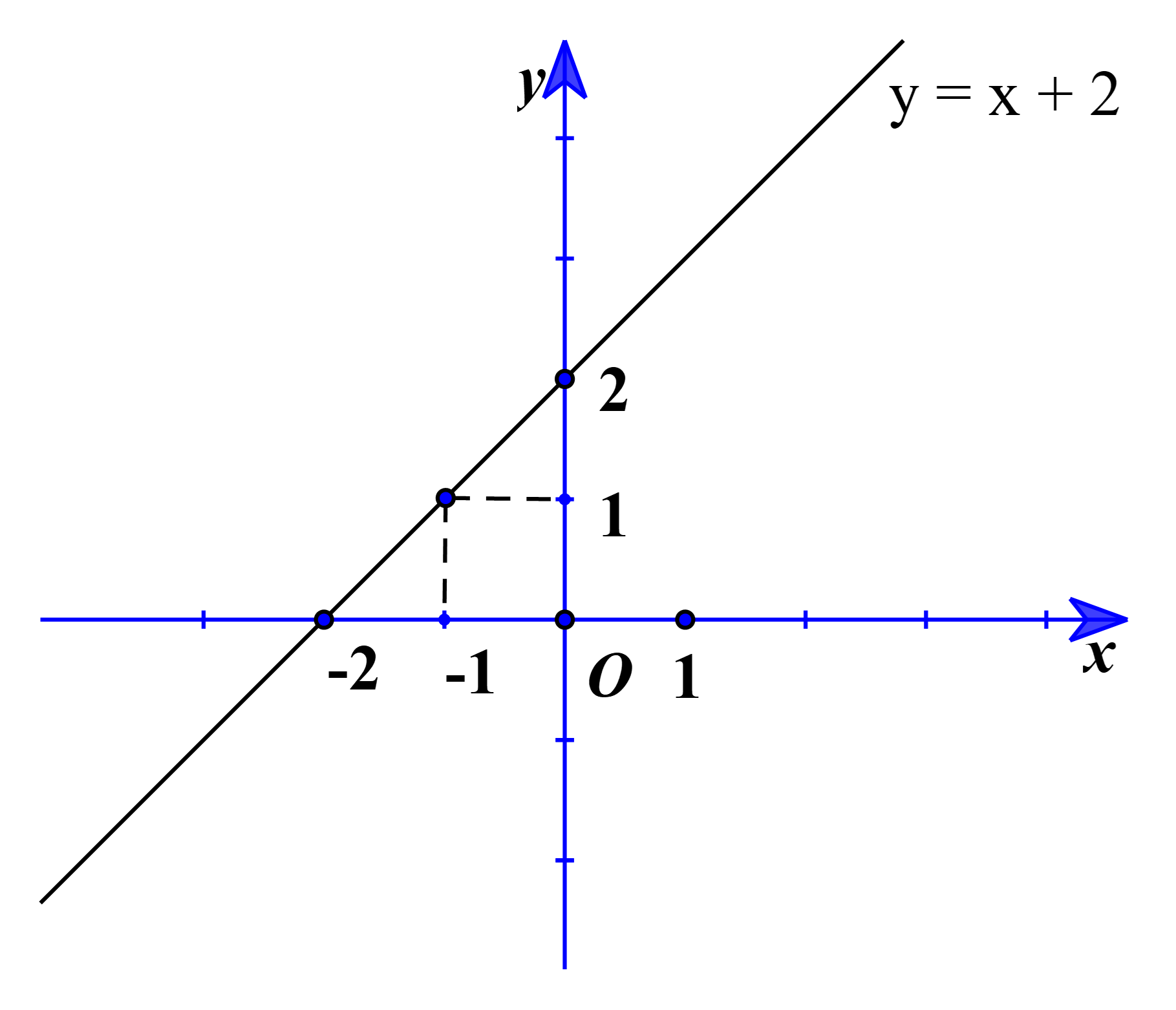
b) Hàm số (1) đồng biến trên ℝ ⇔ 2m – 1 > 0.
\( \Leftrightarrow m > \frac{1}{2}\).
Vậy \(m > \frac{1}{2}\) thỏa mãn yêu cầu bài toán.
c) Phương trình hoành độ giao điểm của d1 và d2: x + 4 = –2x + 7
⇔ 3x = 3 ⇔ x = 1.
Với x = 1, ta có y = 1 + 4 = 5.
Do đó giao điểm của d1 và d2 là A(1; 5).
Để ba đường thẳng d, d1 và d2 đồng quy thì A(1; 5) ∈ dm.
Û 5 = (2m – 1).1 + 2
Û 5 = 2m – 1 + 2
Û 2m = 4
Û m = 2 (nhận)
Vậy m = 2 thỏa mãn yêu cầu bài toán.
Quảng cáo
Bạn muốn hỏi bài tập?



