Các hình trụ tròn xoay có diện tích toàn phần là S không đổi, gọi chiều cao hình trụ là h và bán kính đáy hình trụ là r. Thể tích của khối trụ đó đạt giá trị lớn nhất khi
D. \(h = r\)
Quảng cáo
1 câu trả lời 113
Đáp án C
Phương pháp:
+) Diện tích xung quanh hình trụ tròn xoay: \({S_{xq}} = 2\pi Rl = 2\pi Rh\)
+) Diện tích toàn phần hình trụ tròn xoay:
+) Thể tích khối trụ: \(V = Sh = \pi {R^2}h\)
Cách giải:
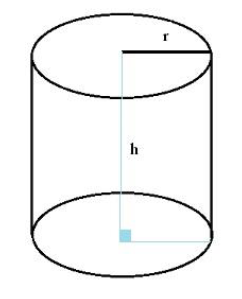
Diện tích toàn phần hình trụ tròn xoay đó là:
\(S = 2\pi rh + 2\pi {r^2} \Rightarrow h = \frac{S}{{2\pi r}} - r\)
Thể tích của khối trụ đó là: \(V = \pi {r^2}h = \pi {r^2}\left( {\frac{S}{{2\pi r}} - r} \right) = \frac{{Sr}}{2} - \pi {r^3}\)
Xét hàm số \(f\left( r \right) = \frac{{Sr}}{2} - \pi {r^3},\,\,r > 0\) có \(f'\left( r \right) = \frac{S}{2} - 3\pi {r^2} = 0 \Rightarrow r = \sqrt {\frac{S}{{6\pi }}} \)
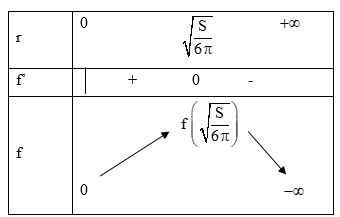
\( \Rightarrow \) Thể tích khối trụ lớn nhất khi
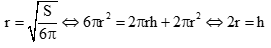
Quảng cáo
Bạn muốn hỏi bài tập?



