Chứng minh rằng đa thức 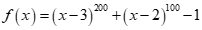 chia hết cho đa thức
chia hết cho đa thức 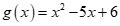
Quảng cáo
1 câu trả lời 756
Tìm cách giải. Đa thức g(x) bậc n có n nghiệm phân biệt. Nếu mọi nghiệm của đa thức g(x) cũng là nghiệm của đa thức f(x) thì đa thức f(x) chia hết cho đa thức g(x). Nhận thấy trong bài g(x) có hai nghiệm là x = 2; x = 3, nên chúng ta chỉ cần kiểm tra xem x= 2; x = 3 có là nghiệm của f(x) không?
Trình bày lời giải
Ta có: ![]() nên
nên ![]()
![]() nên
nên ![]()
Nên f(x) chia hết cho ![]()
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191
Gửi báo cáo thành công!


