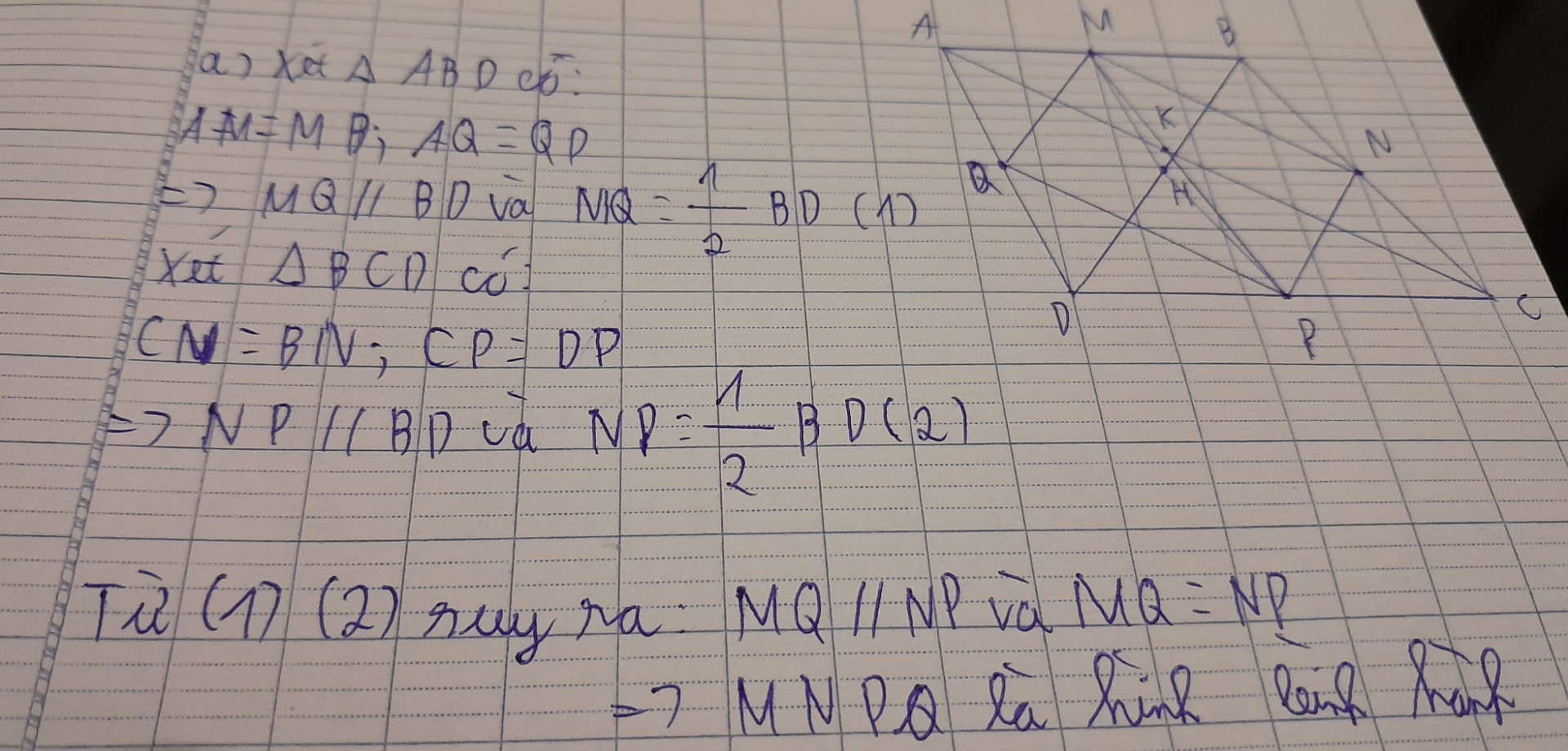-Chứng minh tứ giác MNPQ là hình bình hành.
-Gọi H, K lần lượt là trung điểm của BD, AC. Chứng minh tứ giác MKPH là hình bình hành.
Chứng minh MP, NQ, HK đồng quy
(Giúp mình với ạ)
Quảng cáo
4 câu trả lời 554
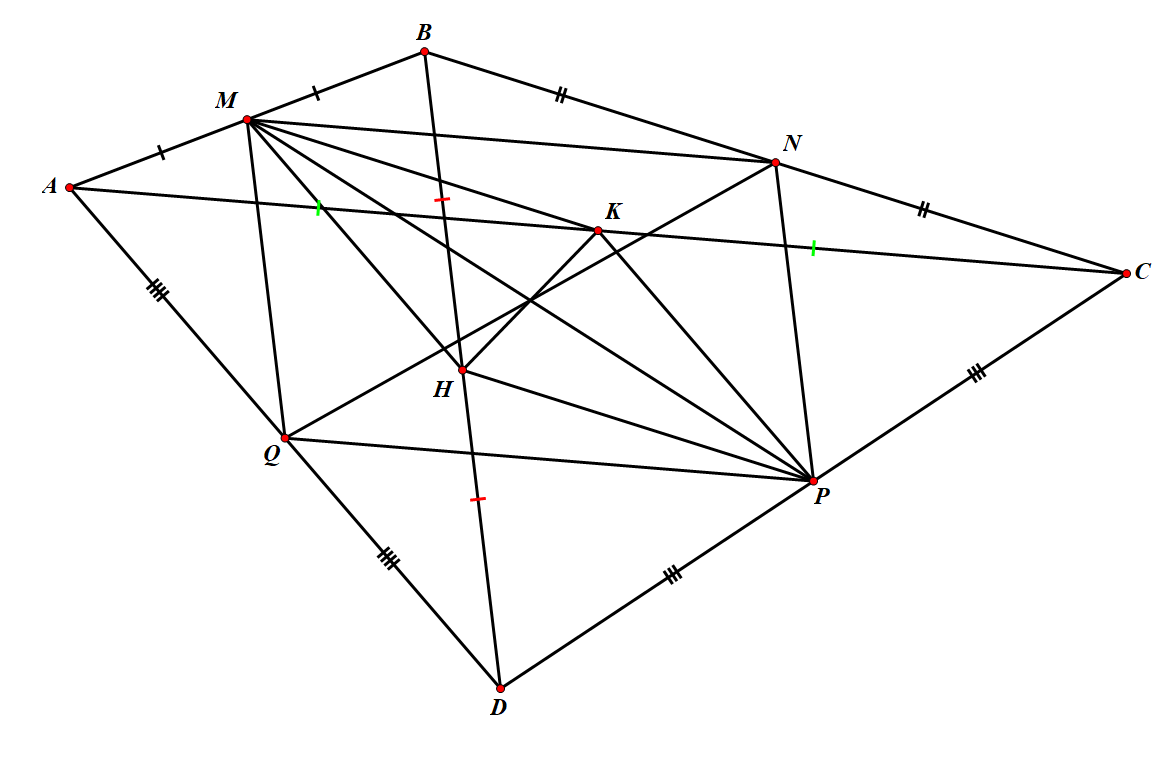
a) Xét ▲ABD:
M là trung điểm AB
Q là trung điểm AD
=> MQ là đường trung bình ▲ABD => MQ // BD, MQ = (1)
Xét ▲BCD có:
N là trung điểm BC
P là trung điểm CD
=> NP là đường trung bình ▲BCD => NP // BD, NP = (2)
Từ (1) và (2) => NP // MQ, NP = MQ
Xét tứ giác MNPQ có: NP // MQ, NP = MQ
=> Tứ giác MNPQ là hình bình hành
b) Xét ▲ABD có:
M là trung điểm AB
H là trung điểm BD
=> HM là đường trung bình ▲ABD => HM // AD, HM = (3)
Xét ▲ACD có:
K là trung điểm AC
P là trung điểm CD
=> KP là đường trung bình ▲ACD => KP // AD, KP = (4)
Từ (3) và (4) => KP // HM, KP = HM
Xét tứ giác MKPH có: KP // HM, KP = HM
=> Tứ giác MKPH là hình bình hành
c) Ta có: tứ giác MKPH là hình bình hành => MP, HK cắt nhau tại trung điểm mỗi đường => HK đi qua trung điểm MP (5)
Ta lại có: tứ giác MNPQ là hình bình hành => MP, QN cắt nhau tại trung điểm mỗi đường => QN đi qua trung điểm MP (6)
Từ (5) và (6) => MP, NQ, HK đồng quy
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191