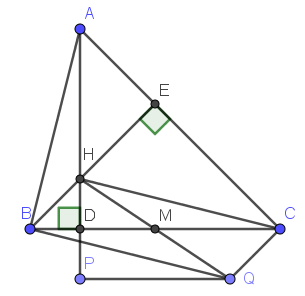
Cho tam giác ABC nhọn. Các đường cao AD và BE cắt nhau tại H. Gọi M là trung điểm của BC. Điểm P đối xứng với H qua đường thẳng BC. Điểm Q đối xứng với Điểm H qua Điểm M.
a) CM: PQ//BC. Khi đó, tứ giác DMQP là hình gì? Vì sao?
b) CM: tứ giác HCQB là hình bình hành. Tính số đó góc ACQ, góc ABQ.
c) Gọi O là giao điểm các đường trung trực của tam giác ABC. CM: điểm O cách đều 5 điểm A,B,P,Q,C.
a) CM: PQ//BC. Khi đó, tứ giác DMQP là hình gì? Vì sao?
b) CM: tứ giác HCQB là hình bình hành. Tính số đó góc ACQ, góc ABQ.
c) Gọi O là giao điểm các đường trung trực của tam giác ABC. CM: điểm O cách đều 5 điểm A,B,P,Q,C.
Quảng cáo
2 câu trả lời 1935
Lời giải:
Vì HH đối xứng với PP qua BCBC nên BCBC là đường trung trực của HPHP, hay HP⊥BCHP⊥BC tại trung điểm của HPHP.
⇒D⇒D là trung điểm của HPHP.
⇒HDDP=1(1)⇒HDDP=1(1)
Mặt khác: HH đối xứng với QQ qua MM nên MM là trung điểm của HQHQ
⇒HMMQ=1(2)⇒HMMQ=1(2)
Từ (1);(2)⇒HDDP=HMMQ(1);(2)⇒HDDP=HMMQ
Theo định lý Talet đảo thì DM∥PQDM∥PQ hay BC∥PQBC∥PQ (đpcm)
b)
Tứ giác DMQPDMQP có DM∥PQDM∥PQ và ˆD=900D^=900 do HP⊥BCHP⊥BC tại DD
Do đó DMQPDMQP là hình thang vuông
c)
Tứ giác HCQBHCQB có hai đường chéo BC,HQBC,HQ cắt nhau tại trung điểm MM của mỗi đường nên là hình bình hành (đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191
Gửi báo cáo thành công!

 hình
hình
