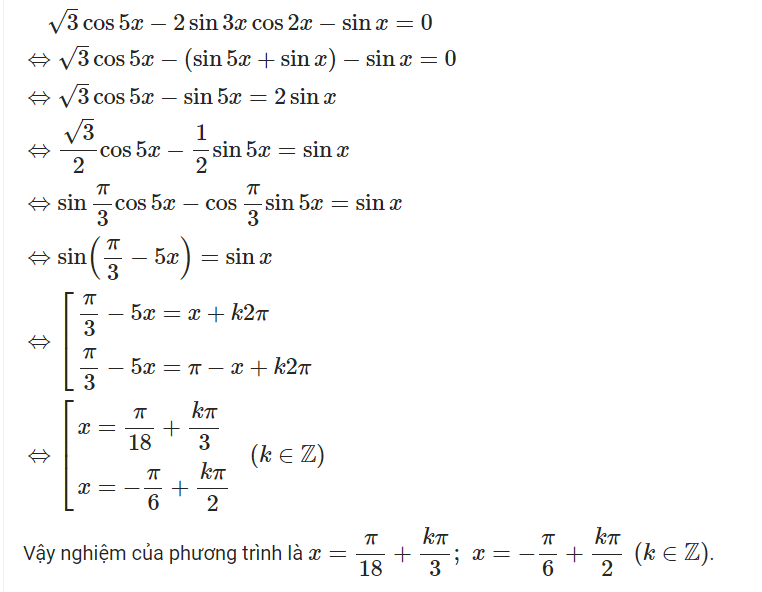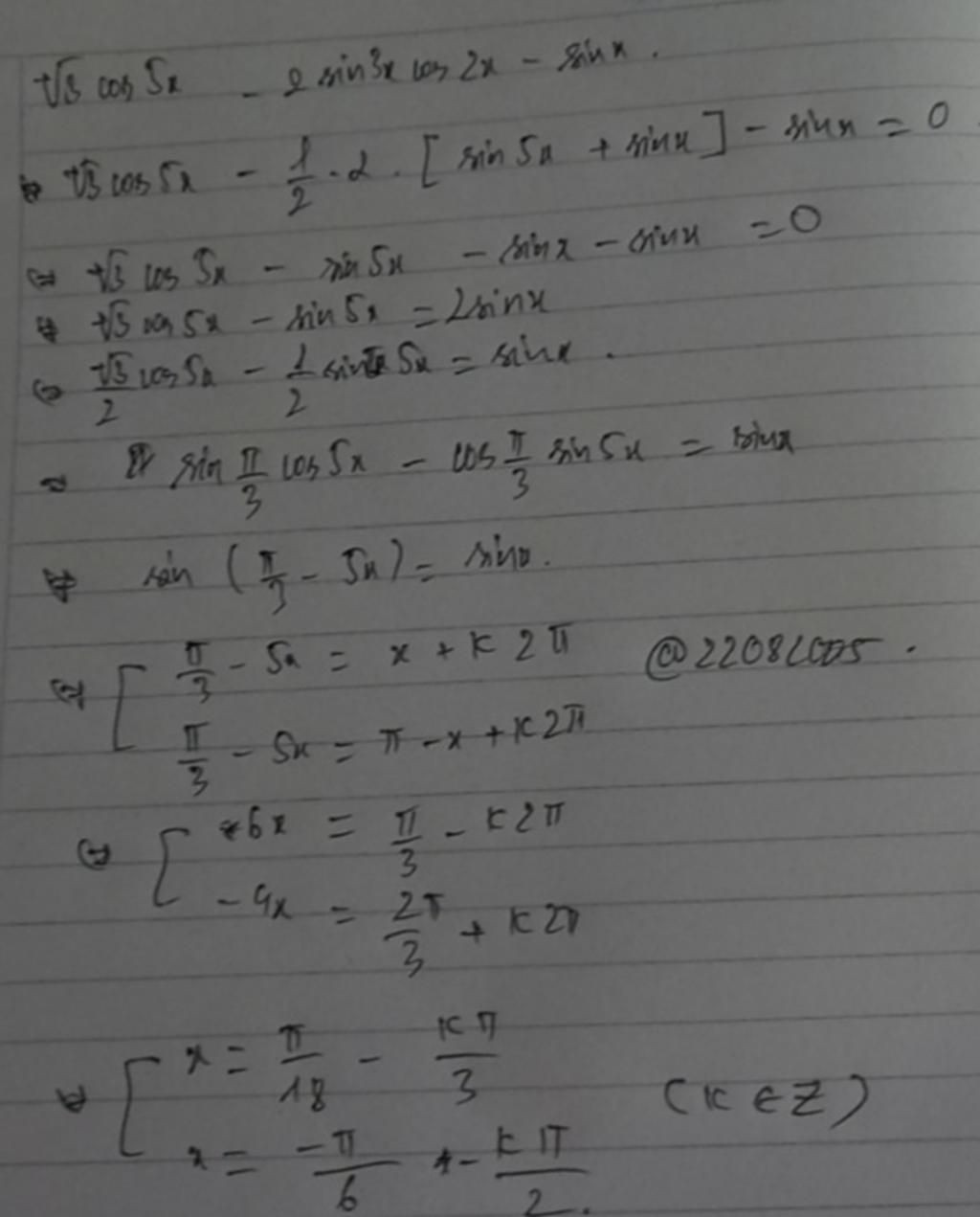
`b)`

$\sqrt3\cos5x - 2\sin3x.\cos2x - \sin x = 0$

$\Leftrightarrow \sqrt3\cos5x - (\sin5x + \sin x) - \sin x = 0$

$\Leftrightarrow \sqrt3\cos5x - \sin5x = 2\sin x$

$\Leftrightarrow \dfrac{\sqrt3}{2}\cos5x - \dfrac12\sin5x = \sin x$

$\Leftrightarrow \sin\left(\dfrac{\pi}{3} - 5x\right)=\sin x$

$\Leftrightarrow \left[\begin{array}{l}\dfrac{\pi}{3} - 5x = x + k2\pi\\\dfrac{\pi}{3} - 5x = \pi - x + k2\pi\end{array}\right.$

$\Leftrightarrow \left[\begin{array}{l}6x = \dfrac{\pi}{3} + k2\pi\\4x = - \dfrac{2\pi}{3} + k2\pi\end{array}\right.$

$\Leftrightarrow \left[\begin{array}{l}x = \dfrac{\pi}{18} + \dfrac{k\pi}{3}\\x = - \dfrac{\pi}{6} + \dfrac{k\pi}{2}\end{array}\right.\quad (k\in\Bbb Z)$

Vậy phương trình có tập nghiệm

$S =\left\{\dfrac{\pi}{18} + \dfrac{k\pi}{3};\ - \dfrac{\pi}{6} + \dfrac{k\pi}{2}\ \Bigg|\ k\in\Bbb Z\right\}$