Quảng cáo
2 câu trả lời 257
ta có:
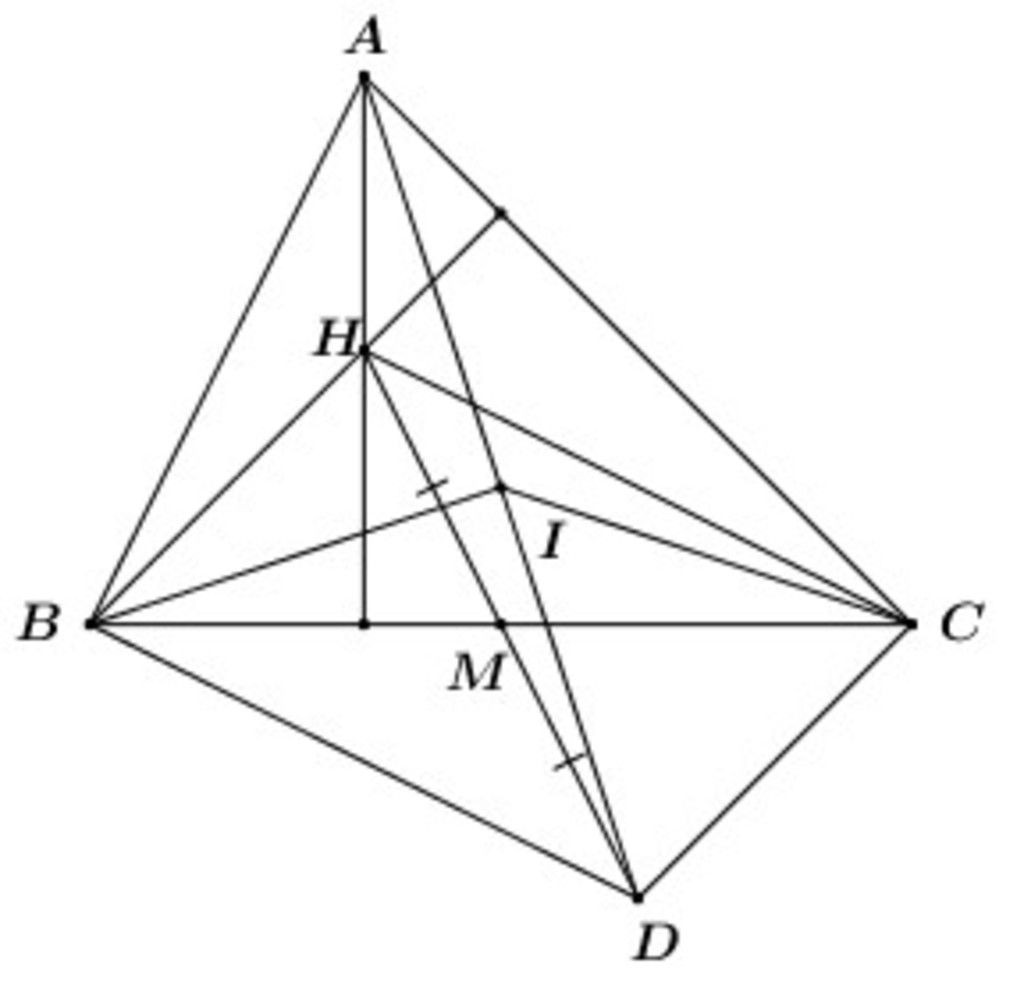
D đối xứng với H qua M => M là trung điểm của HD.
Xét tứ giác BHCD có hai đường chéo BC và HD cắt nhau tại trung điểm mỗi đường.
=> BHCD là hình bình hành (dhnb).
a. BHCD là hình bình hành => BD // CH (tính chất)
H là trực tâm tam giác ABC => CH⊥AB
⇒BD⊥AB =>ΔABD vuông tại B.
Tương tự ta có BHCD là hình bình hành => BH // CD (tính chất).
Mà BH⊥AC (do H là trực tâm tam giác ABC)
⇒CD⊥AC => ΔACD vuông tại C.
b. I là trung điểm của AD ⇒IA=ID=
Tam giác ABD vuông tại B có đường trung tuyến IB ứng với cạnh huyền AD
⇒IB=
Tam giác ACD vuông tại C có đường trung tuyến IC ứng với cạnh huyền AD
⇒IC=
Vậy IA = IB = IC = ID.
D đối xứng với H qua M => M là trung điểm của HD.
Xét tứ giác BHCD có hai đường chéo BC và HD cắt nhau tại trung điểm mỗi đường.
=> BHCD là hình bình hành (dhnb).
a. BHCD là hình bình hành => BD // CH (tính chất)
H là trực tâm tam giác ABC => CH⊥AB
⇒BD⊥AB =>ΔABD vuông tại B.
Tương tự ta có BHCD là hình bình hành => BH // CD (tính chất).
Mà BH⊥AC (do H là trực tâm tam giác ABC)
⇒CD⊥AC => ΔACD vuông tại C.
b. I là trung điểm của AD ⇒IA=ID=
Tam giác ABD vuông tại B có đường trung tuyến IB ứng với cạnh huyền AD
⇒IB=
Tam giác ACD vuông tại C có đường trung tuyến IC ứng với cạnh huyền AD
⇒IC=
Vậy IA = IB = IC = ID
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


