Cho ∆ABC vuông tại A , tia phân giác của góc B cắt AC tại M . Trên cạnh BC lấy D sao cho AD = AB a, chứng minh ∆ABM=∆DBM b, chứng MD vuông góc với BC c, so sánh MC và MA

Phan Phụng Hỏi từ APP VIETJACK

· 09:11 24/05/2022

Cho ∆ABC vuông tại A , tia phân giác của góc B cắt AC tại M . Trên cạnh BC lấy D sao cho AD = AB
a, chứng minh ∆ABM=∆DBM
b, chứng MD vuông góc với BC
c, so sánh MC và MA

Trả Lời (+5 điểm)

Hỏi chi tiết

$\Huge\color{white}{\text{.}}$ · 3 năm trước

đề bài sai nên tớ sửa lại

Quảng cáo

3 câu trả lời 25947

$\Huge\color{white}{\text{.}}$

3 năm trước

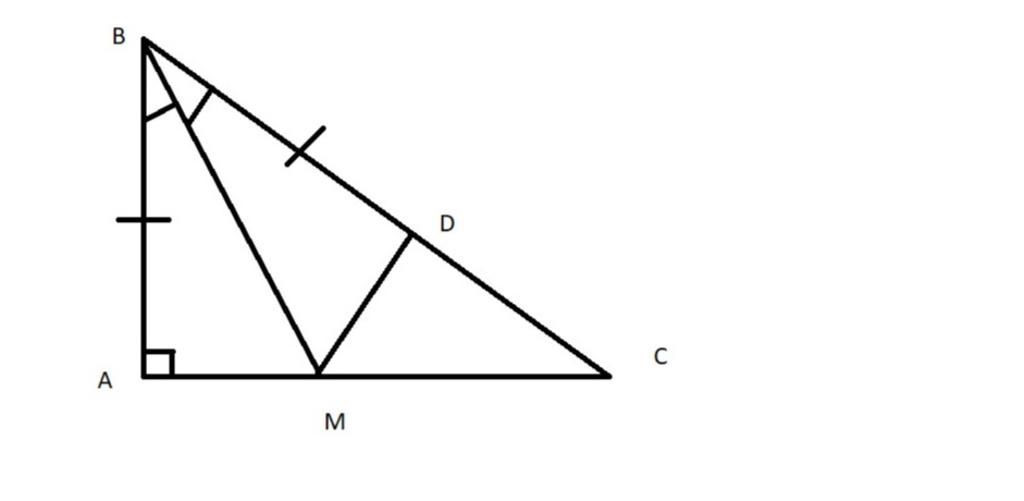
`GT :` $\triangle$ $ABC$ vuông tại $A$

Phân giác $\widehat{ABC}$ $\cap$ $AC$ tại $M$

`D in` BC `( BD = AB )`

$KL :$ `a)` $\triangle$ $ABM =$ $\triangle$ $DBM$

`b) MD` $\bot$ $BC$

`c)` So sánh $MC ; MA$

`a)` Xét $\triangle$ $ABM$ và $\triangle$ $DBM$ ta có $:$

$AB = BD ( gt )$

$\widehat{ABM}$ $=$ $\widehat{DBM}$ $($ vì $BM$ là tia phân giác của $\widehat{ABC}$ $)$

$BM$ chung

`=>` $\triangle$ $ABM =$ $\triangle$ $DBM ( c - g - c )$

`b)` Ta có $:$ $\widehat{BAM}$ $=$ $\widehat{BDM}$ $($ vì $\triangle$ $ABM =$ $\triangle$ $DBM )$
Mà $\widehat{BAM}$ $= 90^o ($ vì $\triangle$ $ABC$ vuông tại $A )$

`=>` $\widehat{BDM} = 90^o$

`=> MD` $\bot$ $BC$

`c)` Vì `MD` $\bot$ $BC ( cmt )$

`=>` $\widehat{MDC}$ $= 90^o$

`=>` $\triangle$ $MDC$ vuông tại $D$

`=> MC > MD ( ch > cgv )`

Mà $MD = MA ($ vì $\triangle$ $ABM =$ $\triangle$ $DBM )$

`=> MC > MA`

...Xem thêm

8 bình luận

3 ( 2.3 )

Huong NGuyen · 1 năm trước

Bọn m bị ngu à. Ad = ab chứ có phải ab=bd đâu

...Xem tất cả bình luận

Đăng nhập để hỏi chi tiết

Pham Thi Phuong Thao

3 năm trước

a,Xét $∆$ ABM và $∆$ DBM có :

AB=DB(gt)

BM chung

góc ABM = góc DBM

suy ra $∆$ ABM = $∆$ DBM ( c.g.c)

b,Theo câu a có : tam giác ABM = tam giác DBM nên :

suy ra góc MAB = góc MDB =90 $°$

suy ra MD vuông góc BC

c, Có MA=MD(theo câu a) (1)

Xét tam giác CDM có :

$∠$ MDC > $∠$ MCD

suy ra MC > MD(theo tính chất của cạnh và góc đối diện ) (2)

tỪ (1), (2) suy ra MA<MC

9 bình luận

2 ( 5.0 )

Phan Phụng · 3 năm trước

Làm cho mình gt vs kl đc ko bn

manh ngoduc · 10 tháng trước

a,Xét incrementABM và incrementDBM có : AB=DB(gt) BM chung góc ABM = góc DBM suy ra incrementABM = incrementDBM ( c.g.c) b,Theo câu a có : tam giác ABM = tam giác DBM nên : suy ra góc MAB = góc MDB =90degree suy ra MD vuông góc BC c, Có MA=MD(theo câu a) (1) Xét tam giác CDM có : angleMDC > angleMCD suy ra MC > MD(theo tính chất của cạnh và góc đối diện ) (2) tỪ (1), (2) suy ra MA<MC Cảm ơn(+4) 7 1 ( 5.0 ) Phan Phụng · 2 năm trước Làm cho mình gt vs kl đc ko bn ...Xem tất cả bình luận m ad Quảng cáo Câu hỏi hot cùng chủ đề ad Cho capital delta A B C có AB < AC. Kẻ tia phân giác AD của stack B A C with hat on top (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng: a) capital delta B D F equals capital delta E D C semicolon b) F, D E thẳng hàng; c) A D perpendicular F C Trả lời (28) 25 142412 Điểm cách đều ba cạnh của tam giác là: A. Giao điểm của ba đường cao B. Giao điểm của ba đường trung trực C. Giao điểm của ba đường trung tuyến D. Giao điểm của ba đường phân giác Trả lời (224) 9 72909 Cho incrementABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME=MA. Chứng minh rằng: a/ AC=EB và AC // BE b/ Gọi I là một điểm trên AC, K là một điểm trên EB sao cho: AI=EK. Chứng minh: I, M, K thẳng hàng. c/ Từ E kẻ EH perpendicular BC (H element of BC). Biết góc stack H B E with hat on top bằng 50degree; stack M E B with hat on top bằng 25degree, tính các góc stack H E M with hat on top và stack B M E with hat on top ? Trả lời (15) 6 70524 ad Cho tam giác ABC vuông tại A, đường phân giác BE. Kẻ EH vuông góc với BC (H thuộc BC). Gọi K giao điểm của AB và HE. Chứng minh rằng: a, increment A B E equals increment H B E b, BE là đường trung trực của đoạn thẳng AH c, EK=EC d, AE<EC. Trả lời (49) 10 56012 Cho triangleABC cân tại A (A with hat on top less than 90 to the power of degree). Kẻ BD perpendicular AC tại D, kẻ CE ⊥ AB tại E. a) Chứng minh △ADE cân b) chứng minh DE // BC c) Gọi I là giao điểm của BD và CE. Chứng minh IB = IC d) Chứng minh AI ⊥ BC Trả lời (3) 2 52320 Cho tam giác ABC có ba góc nhọn (AB<AC). Vẽ về phía ngoài tam giác ABC các tam giác đều ABD và ACE. Gọi I là giao điểm của CD và BE, K là giao điểm của AB và DC. a) Chứng minh rằng: capital delta A D C equals capital delta A B E b) Chứng minh rằng: stack D I B with hat on top equals 60 degree c) Gọi M và N lần lượt là trung điểm của CD và BE. Chứng minh rằng capital delta A M N đều d) Chứng minh rằng IA+IB=ID e) Chứng minh rằng IA là tia phân giác của góc DIE. Trả lời (5) 9 42189 ad Hỏi từ APP VIETJACK Cho tam giác ABC vuông tại A có AB bé hơn AC, kẻ đường phân giác BD của ABC, (D thuộc AC). Kẻ DM vuông góc với BC tại M a) CM tam giác DAB = tam giác DMB b) CM AD bé hơn DC c) Gọi K là giao điểm của đường thẳng DM và đường thẳng AB, đường thẳng BD cắt KC tại N. CM BN vuông góc KC và tam giác KDC cân tại B Trả lời (10) 6 41742 Cho tam giác ABC cân có AB=AC=5cm, BC= 8cm. Kẻ AH vuông góc với BC (H thuộc BC). a, Chứng minh HB=HC b, Tính độ dài AH. c, Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC). Chứng minh tam giác HDE cân. d, So sánh HD và HC. Trả lời (3) 6 36242 2 góc tương ứng là gì? Trả lời (64) 21 34978 ad Phát biểu định lý Pytago thuận và đảo ? Trả lời (33) 9 30126 m manh ngoduc Số câu trả lời: 0 Cấp bậc: Số điểm:0 Bài viết mới nhất Lớp 7 Sách bài tập Lịch sử 7 Chân trời sáng tạo Bài 16: Công cuộc xây dựng đất nước thời Trần (1226-1400) 1 năm trước 3019 Sách bài tập Lịch sử 7 Chân trời sáng tạo Bài 15: Công cuộc xây dựng và bảo vệ đất nước thời Lý (1009-1225) 1 năm trước 2485 Sách bài tập Lịch sử 7 Chân trời sáng tạo Bài 14: Công cuộc xây dựng và bảo vệ đất nước thời Ngô - Đinh - Tiền Lê (938-1009) 1 năm trước 2659 Sách bài tập Lịch sử 7 Chân trời sáng tạo Bài 13: Vương quốc Lào 1 năm trước 2196 Sách bài tập Lịch sử 7 Chân trời sáng tạo Bài 12: Vương quốc Cam-pu-chia 1 năm trước 2284 Xem thêm » Gửi báo cá