Cho tam giác ABC cân tại A, đường cao BD và CE cắt nhau tại H.CMR
a)BD=CE
b)tam giác BHC cân
c)AH là đường trung trực của BC
Quảng cáo
2 câu trả lời 3587
a) xét tam giác BEC và tam giác CDB có
BC chung
BEC=CDB(=90 độ)
ABC=ACB( tam giác ABC cân A)
=> tam giác BEC= tam giác CDB(ch-gnh)
=> BD=CE( hai cạnh tương ứng)
b) từ tam giác BEC= tam giác CDB=> DBC=ECB(hai góc tương ứng)
=> tam giác HBC cân H
c) đặt O là giao điểm của AH với BC
vì AH,BD,CE cùng giao nhau tại H mà BD, CE là đường cao=> AH là đường cao ( 3 đường cao cùng đi qua một điểm)
vì HBC cân H=> HB=HC
xét tam giác HOB và tam giác HOC có
HB=HC(cmt)
HBO=HCO(cmt)
HOB=HOC(=90 độ)
=> tam giác HOB= tam giác HOC(ch-gnh)
=> BO=CO( hai cạnh tương ứng)
=> AH là trung trực của BC
Mình gửi bạn
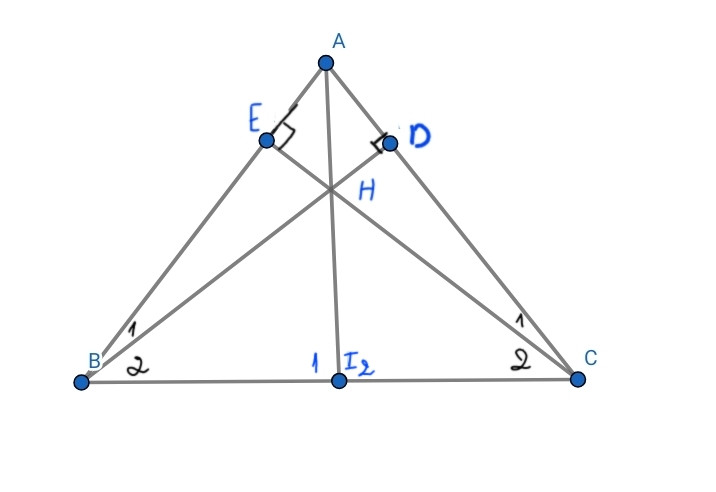
a
Xét ∆ABD vuông tại D và ∆ACE vuông tại E, ta có:
AB = AC ( ∆ABC cân tại A )
^BAC: góc chung
=> ∆ABD = ∆ACE ( cạnh huyền - góc nhọn )
=> BD = CE ( 2 cạnh tương ứng )
b.
Ta có:
^B1 + ^B2 = ^B
^C1 + ^C2 = ^C
Mà: ^B1 = ^C1 ( ∆ABD = ∆ACE )
=> ^B2 = ^C2
=> ∆ BHC cân tại H
c.
Vì ∆BHC cân tại H ( câu b )
=> BH = CH
=> AH là phân giác ^BAC ( định lý 2 )
Hay AI là phân gíc ^BAC
=> IB = IC ( định lý 1 )
=> I là trung điểm BC ( 1 )
Xét ∆ BAI và ∆CAI, ta có:
AB = AC ( ∆ABC cân tại A )
AI: chung
IB = IC ( cmt )
=> ∆BAI = ∆CAI ( c.c.c )
=> ^I1 = ^I2 ( 2 góc tương ứng )
Mà: ^I1 + ^I2 = 180⁰ ( kề bù )
=> ^I1 = ^I2 = 180⁰/2 = 90⁰
=> AI vuông góc BC (2)
Từ (1) và (2), ta suy ra: AI là trung trực BC hay AH là trung trực BC
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12423
-
 Đã trả lời bởi chuyên gia
5747
Đã trả lời bởi chuyên gia
5747 -
4835


