Bài 3. (4,0 điểm) Cho X0y nhon, Om là tia phân giác của xOy. Trên tia Ox lấy điểm I, qua I kẻ đường thẳng vuông góc với Om cắt tia Ox, Oy lần lượt tại A và B.
1) Chứng minh rằng AOAI = AOBI và AOAB cân.
2) Trên tia Ax lấy điểm M, trên tia By lấy điểm N, sao cho AM = BN.
Chứng minh rằng AOMN cân và AB//MN.
3) Trên tia đối của tia ly lấy điểm K sao cho OA = OB, Đường thẳng vuông góc với Om tại 0 cắt AK tại H. Chứng minh rằng OH là tia phân giác của KOA.
4) Tia KA cắt MN tại D. Chứng minh rằng: DA+DK< 2ON.
HELP PLSSSS
Quảng cáo
1 câu trả lời 297
Mình gửi bạn cách giải
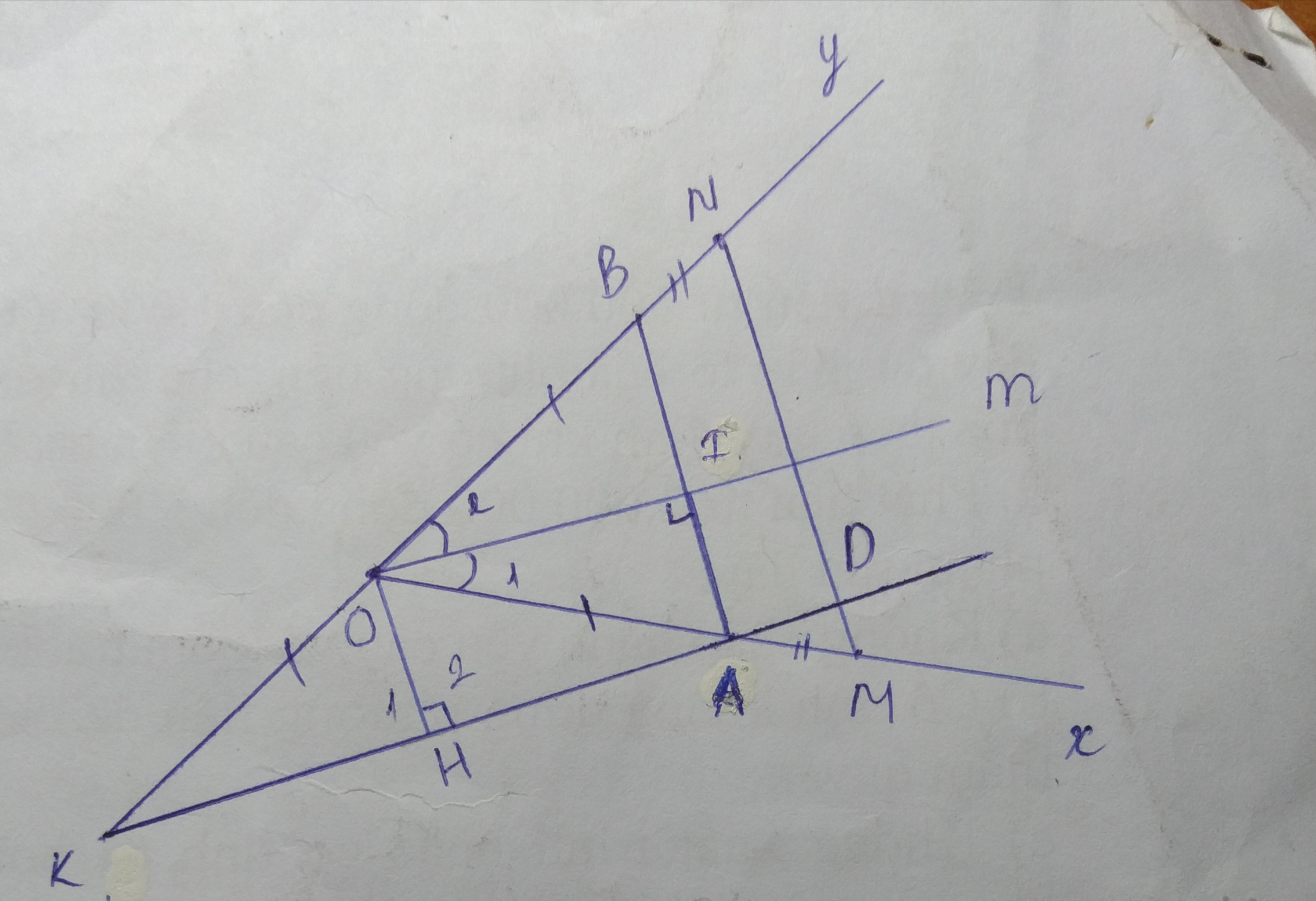


d.
Ta có: AD ⊥ MN
=> AD < AM ( quan hệ giữa đường vuông góc và đường xiên )
lại có: AM = BN
=> AD < BN
=> 2AD < 2BN (***)
Ta lại có: ∆OHA ⊥ H
=> HA < OA ( trong một tam giác vuông, cạnh huyền là cạnh lớn nhất )
Mà: OA = OB
=> HA < OB
Ta có:
HA = HK ( ∆OHK = ∆ OHA )
=> HK < OB
=> HA + HK < 2OB (****)
=> Từ (***), (****)
KH + HA + 2AD < 2 (OB + BN )
DA + DA < 2BN
Quảng cáo
Câu hỏi hot cùng chủ đề
-
8 74277
-
9 49098
-
Hỏi từ APP VIETJACK7 46021



