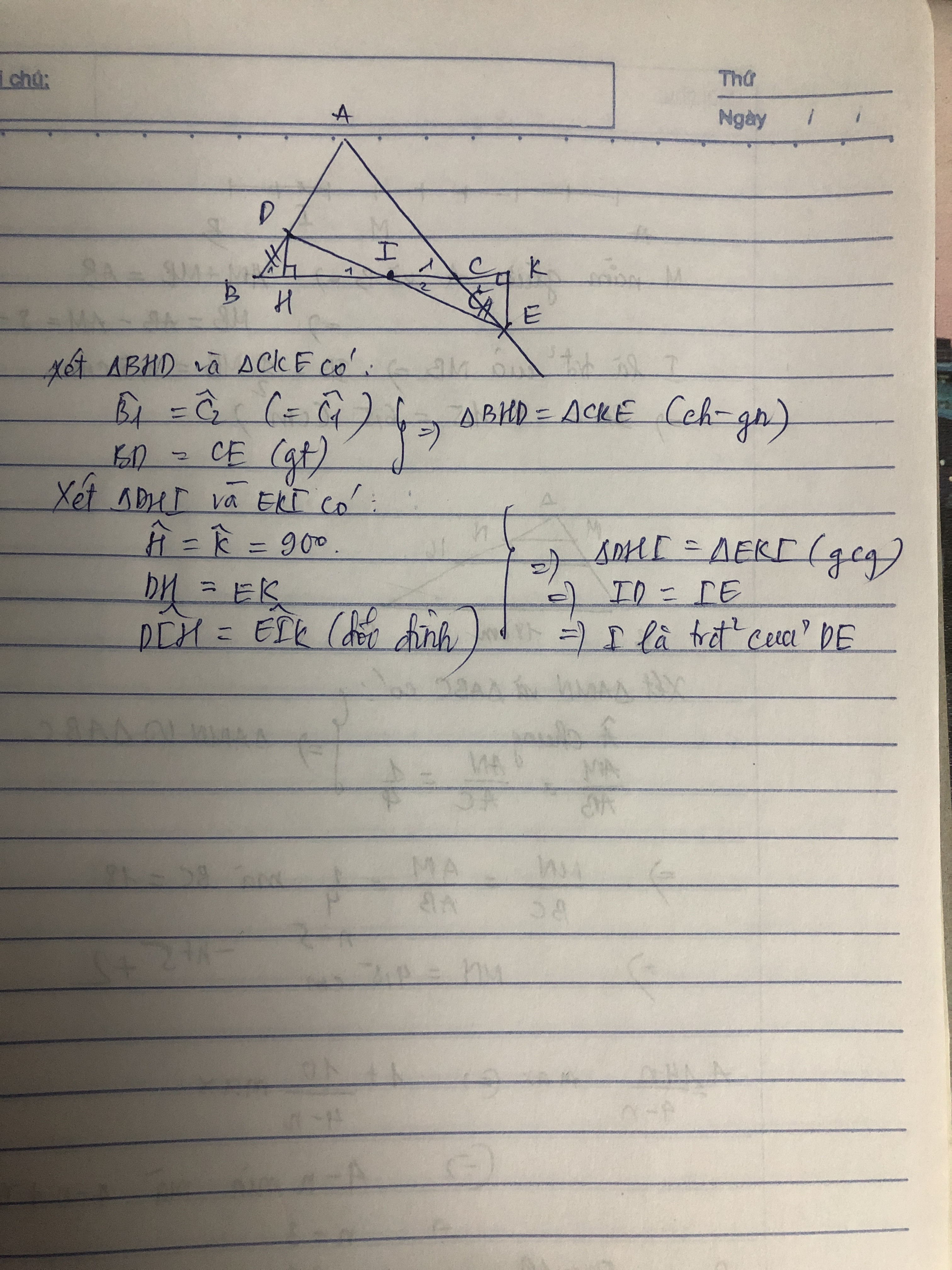a, chứng minh dh=ek
b, gọi i là giao điển của de và bc. chứng minh i là trung điển của de
Quảng cáo
3 câu trả lời 511
a) Ta có : ˆABC=ˆACBABC^=ACB^ (tam giác ABC cân tại A)
Lại có : ˆKCE=ˆACBKCE^=ACB^ (đối đỉnh)
Suy ra : ˆABC=ˆKCE(=ˆACB)ABC^=KCE^(=ACB^)
Xét ΔDBH,ΔECKΔDBH,ΔECK có :
ˆDBH=ˆECKDBH^=ECK^ (do ˆABC=ˆKCEABC^=KCE^)
BD=CE(gt)BD=CE(gt)
ˆDHB=ˆEKC(=90o)DHB^=EKC^(=90o)
=> ΔDBH=ΔECKΔDBH=ΔECK (cạnh huyền -góc nhọn)
=> DH = EK (2 cạnh tương ứng)
b) Xét ΔDHI,ΔEKIΔDHI,ΔEKI có :
ˆDHI=ˆEKI(=90o)DHI^=EKI^(=90o)
DH=EK(cmt)DH=EK(cmt)
ˆDIH=ˆEIKDIH^=EIK^ (đối đỉnh)
=> ΔDHI=ΔEKI(g.c.g)ΔDHI=ΔEKI(g.c.g)
=> DI = EI (2 cạnh tương ứng)
=> I là trung điểm của DE
=> đpcm.
a) Ta có : ˆABC=ˆACB (tam giác ABC cân tại A)
Lại có : ˆKCE=ˆACB(đối đỉnh)
Suy ra : ˆABC=ˆKCE(=ˆACB)
Xét ΔDBH,ΔECK có :
ˆDBH=ˆECK (do ˆABC=ˆKCE)
BD=CE(gt)
ˆDHB=ˆEKC(=90o)
=> ΔDBH=ΔECK (cạnh huyền -góc nhọn)
=> DH = EK (2 cạnh tương ứng)
b) Xét ΔDHI,ΔEKI có :
ˆDHI=ˆEKI(=90o)
DH=EK(cmt)
ˆDIH=ˆEIK (đối đỉnh)
=> ΔDHI=ΔEKI(g.c.g)
=> DI = EI (2 cạnh tương ứng)
=> I là trung điểm của DE
=> đpcm.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515