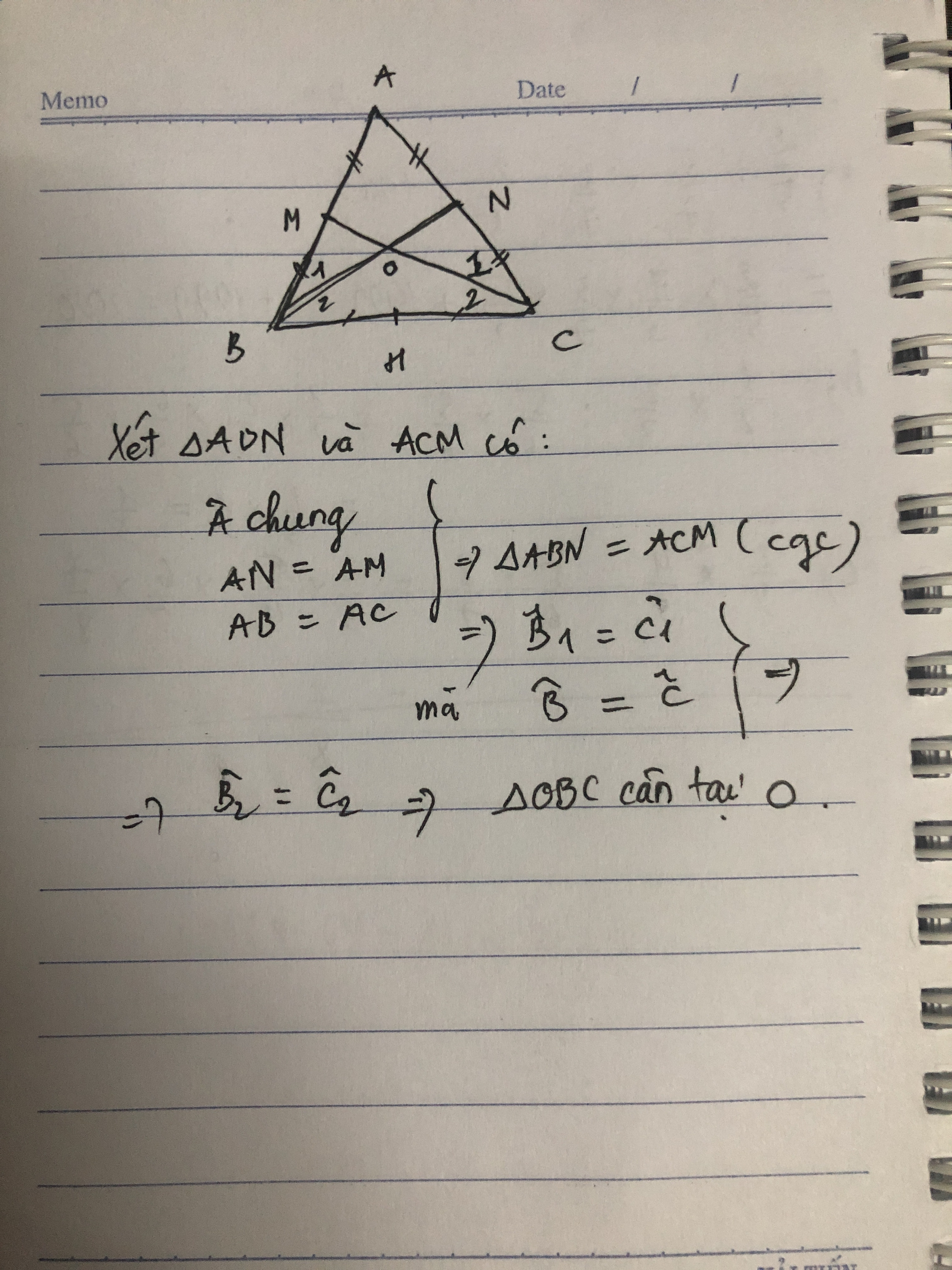Cho ∆ABC cân tại A.Gọi M,N lần lượt là trung điểm của AB,AC.H là trung điểm của BC.
a)Chứng minh:∆ABN=∆ACM.
b)BN cắt CM tại O.Chứng minh:∆OBC cân.
Quảng cáo
2 câu trả lời 586
a) Ta có : {M∈AC(M là trung điểm của AC)N∈AB(N là trung điểm của AB)⇒{AN=BNAM=CM{M∈AC(M là trung điểm của AC)N∈AB(N là trung điểm của AB)⇒{AN=BNAM=CM
Lại có : AB = AC (ΔABCΔABC cân tại A)
Suy ra : AN=BN=AM=CM(=AB2)AN=BN=AM=CM(=AB2)
Xét ΔNBC,ΔMCBΔNBC,ΔMCB có :
BN=CM(cmt)BN=CM(cmt)
ˆNBC=ˆMCBNBC^=MCB^ (ΔABCΔABC cân tại A)
BC:ChungBC:Chung
=> ΔNBC=ΔMCB(c.g.c)ΔNBC=ΔMCB(c.g.c)
=> BM = CN BM = CN (2 cạnh tương ứng)
Xét ΔABM,ΔACNΔABM,ΔACN có :
AB=ACAB=AC (ΔABCΔABC cân tại A)
ˆA:chungA^:chung
AM=ANAM=AN (cmt)
=> ΔABM=ΔACN(c.g.c)ΔABM=ΔACN(c.g.c)
=> ˆABM=ˆACNABM^=ACN^ (2 góc tương ứng)
b) Từ ΔNBC=ΔMCB(cmt)ΔNBC=ΔMCB(cmt) ta có :
ˆNCB=ˆMBCNCB^=MBC^ (2 góc tương ứng)
Hay : ˆICB=ˆIBCICB^=IBC^
=> ΔIBCΔIBC cân tại I
d) Xét ΔAIB,ΔAICΔAIB,ΔAIC có :
AB=ACAB=AC (ΔABCΔABC cân tại A)
AI:Chung
IB=ICIB=IC ( ΔIBCΔIBC cân tại I)
=> ΔAIB=ΔAIC(c.c.c)ΔAIB=ΔAIC(c.c.c)
=> ˆBAI=ˆCAIBAI^=CAI^ (2 góc tương ứng)
=> AI là tia phân giác của ˆBACBAC^
Hay : AI là tia phân giác của ˆAA^
d) Ta có : AI∩BC={M}AI∩BC={M}
Xét ΔAMB,ΔAMCΔAMB,ΔAMC có :
AB=ACAB=AC (tam giác ABC cân tại A)
ˆBAM=ˆCAMBAM^=CAM^ (AI là tia phân giác của góc A)
AM : Chung
=> ΔAMB=ΔAMC(c.g.c)ΔAMB=ΔAMC(c.g.c)
=> ˆAMB=ˆAMCAMB^=AMC^ (2 góc tương ứng)
Mà : ˆAMB+ˆAMC=180O(Kềbù)AMB^+AMC^=180O(Kềbù)
=> ˆAMB=ˆAMC=180O2=90OAMB^=AMC^=180O2=90O
=> AM⊥BCAM⊥BC
Hay : AI⊥BCAI⊥BC (do M∈AIM∈AI - cách vẽ)
=> đpcm
ΔABC
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515