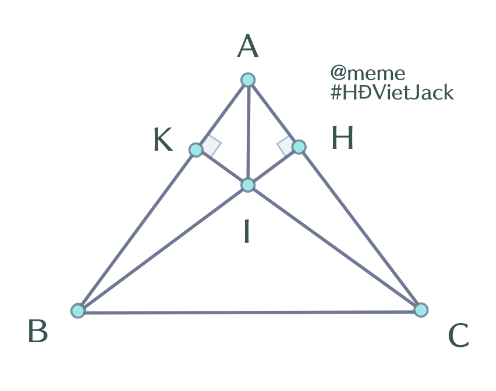
Kẻ BH vuông góc AC (H thuộc AC)
CK vuông góc AB (K thuộc AB)
Chứng minh : AK = AH
b. Gọi I là giao điểm của BH và CK
Chứng minh AI là tia phân giác góc BAC
Quảng cáo
2 câu trả lời 2498
`a)`
Xét `2triangle` vuông: `triangleABH` và `triangleACK` có:
`hat{ABH}=hat{AKC}=90^o`
`AB=AC` (do `triangleABC` cân tại `A`)
`hatA` là góc chung
`totriangleABH=triangleACK` (cạnh huyền- góc nhọn)
`toAK=AH` (`2` cạnh tương ứng)
`b)`
Xét `2triangle` vuông: `triangleAKI` và `triangleAHI` có:
`hat{AKI}=hat{AHI}=90^o`
`AK=AH` (cmt)
`AI` là cạnh chung
`totriangleAKI=triangleAHI` (cạnh huyền- cạnh góc vuông)
`tohat{IAK}=hat{IAH}` (`2` góc tương ứng)
`toIA` là phân giác `hat{KAH}`
mà `KinAB,HinAC`
`toIA` là phân giác `hat{BAC}`
a) Xét △ABH và △ACK có:
AHB = AKC (= 90o)
AB = AC (△ABC cân)
KAH: chung
=> △ABH = △ACK (ch-gn)
=> AH = AK (2 cạnh tương ứng)
b) Xét △AIK và △AIH có:
AKI = AHI (= 90o)
AI: chung
AK = AH (cmt câu a)
=> △AIK = △AIH (ch-cgv)
=> IAK = IAH (2 góc tương ứng)
=> AI là phân giác BA
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515


