27-Lê Phước Thành Tài
Hỏi từ APP VIETJACK
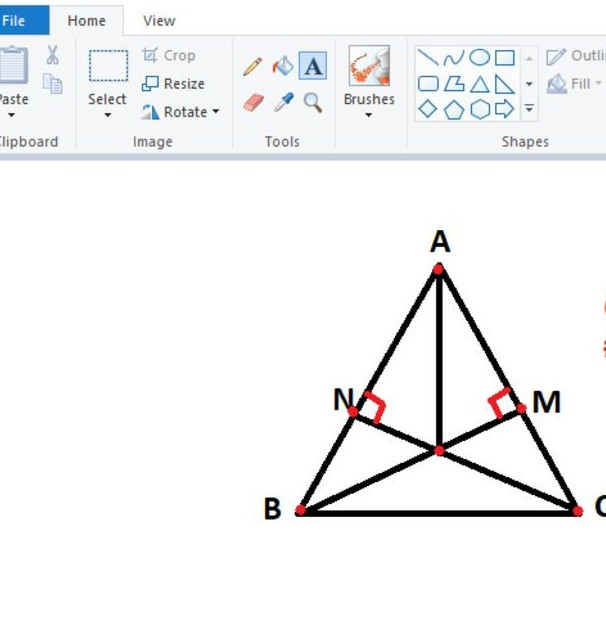
Cho ∆ABC cân tại A. Kẻ BM vuông góc AC( M thuộc AC), CN vuông góc AB (N thuộc AB)
a) Chứng minh: ∆BMC = ∆CNB
b) Gọi I là giao điểm của BM và CN
Chứng minh:∆AIN=∆AIM
a) Chứng minh: ∆BMC = ∆CNB
b) Gọi I là giao điểm của BM và CN
Chứng minh:∆AIN=∆AIM
Quảng cáo
1 câu trả lời 1808
3 năm trước
a,
Xét △BMC và △CNB , ta có :
ˆBMC = ˆCNB( = 90)
BC cạnh chung
ˆMBC = ˆNCB ( △ABCcân tại A)
⇒ △BMC = △CNB (ch−gn)
b,
Vì △BMC = △CNB
⇒NB=MC( hai cạnh tương ứng)
Ta có :
AN+NB=AB
AM+MC=AC
Mà AB=AC ( △ABC cân tại A) và NB=MC(cmt)
⇒AN=AM
Xét △AINvà △AIM, ta có :
ˆANI = ˆAMI ( = 90o90o)
AI cạnh chung
AN=AM (cmt)
⇒ △AIN = △AIM (ch−cgv)
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515
Gửi báo cáo thành công!


