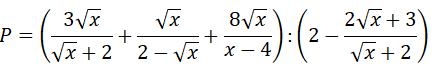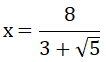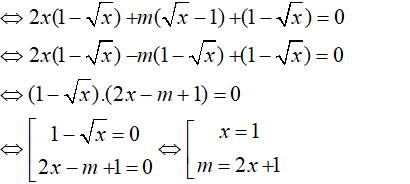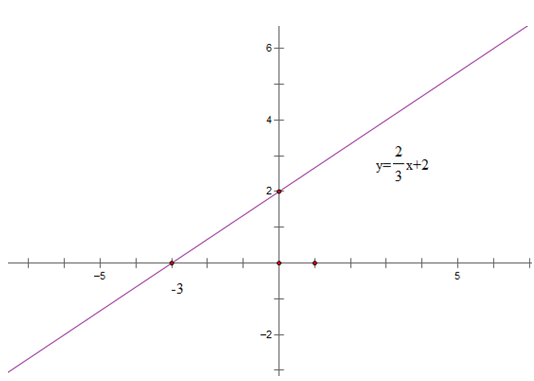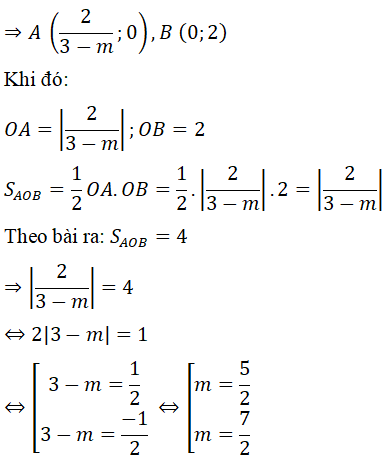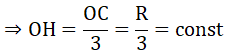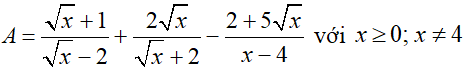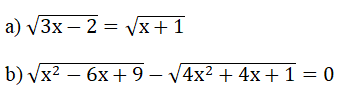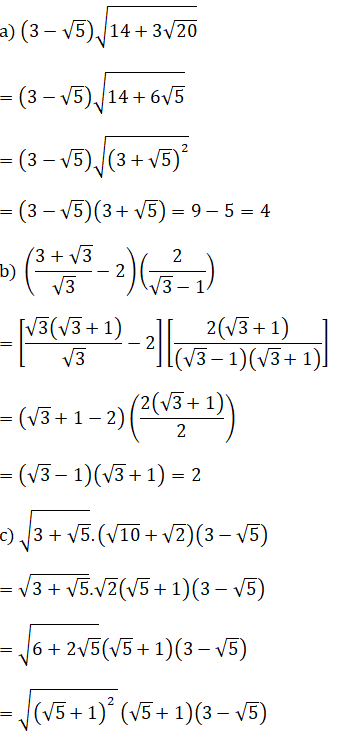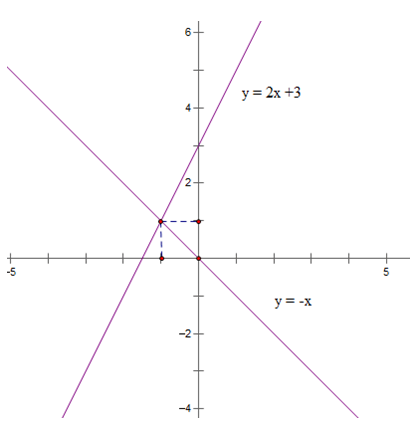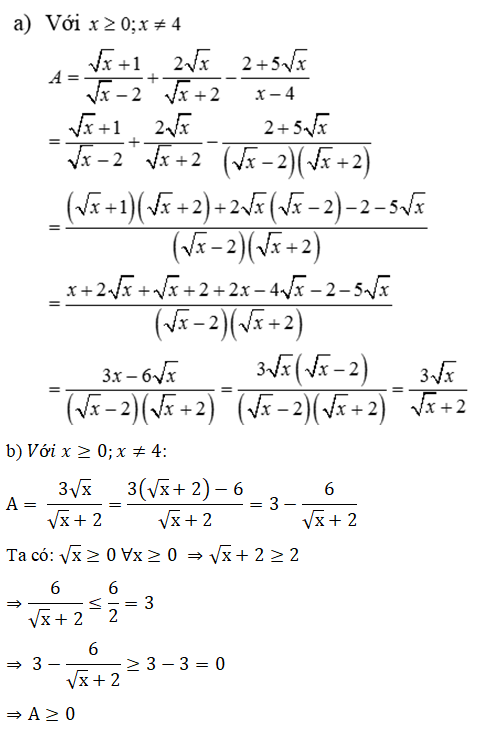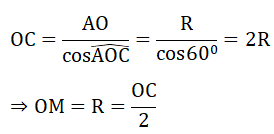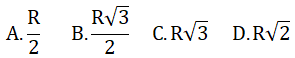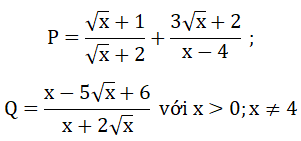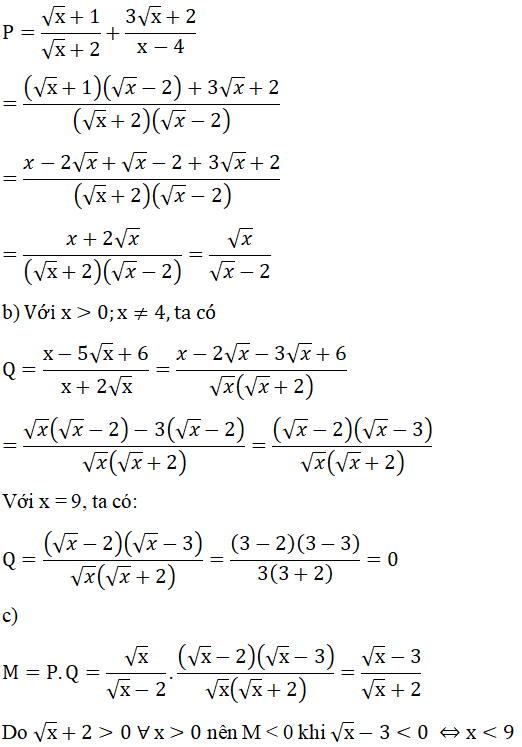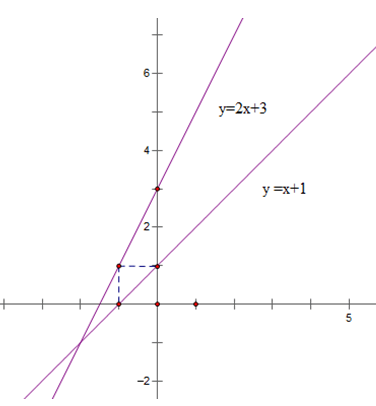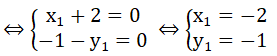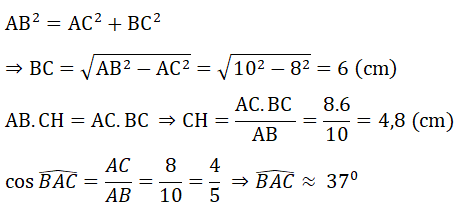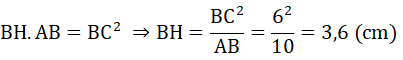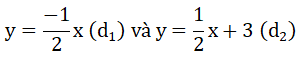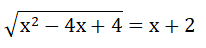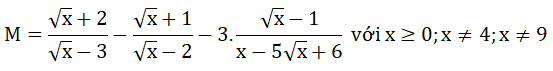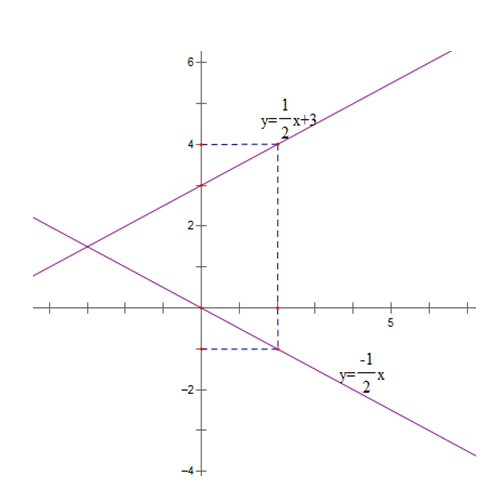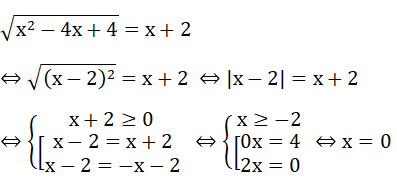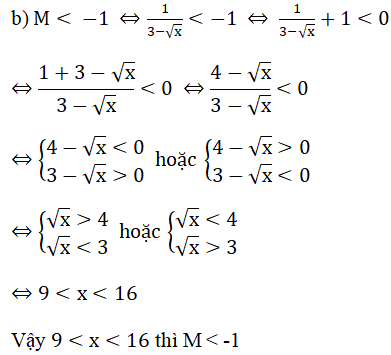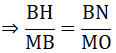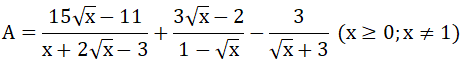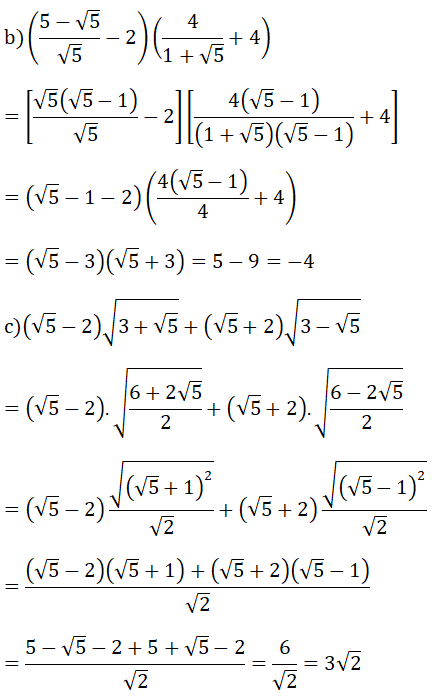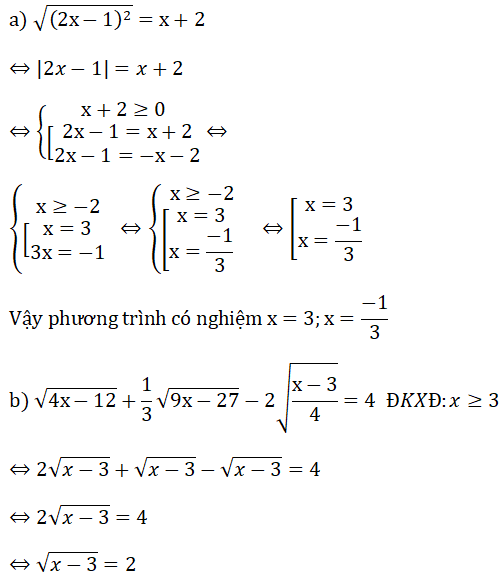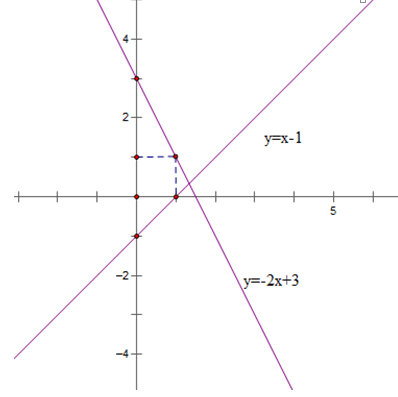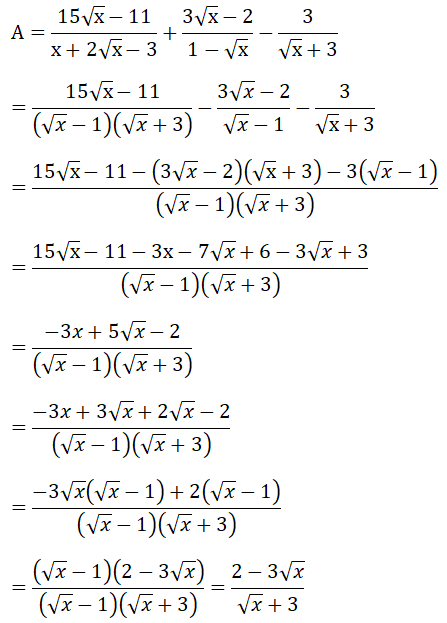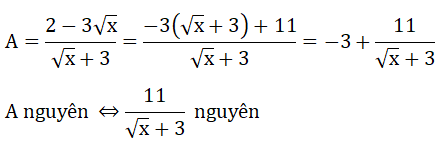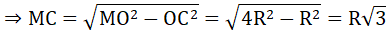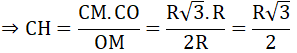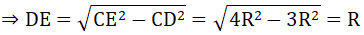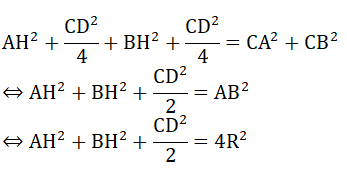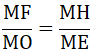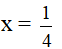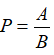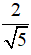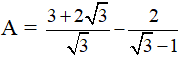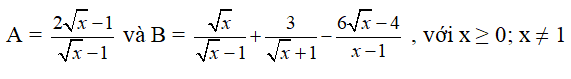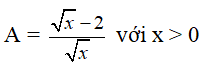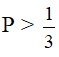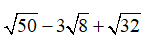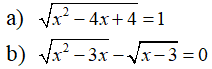Bộ 30 đề thi Học kì 1 Toán lớp 9 có đáp án
Bộ 30 đề thi Học kì 1 Toán lớp 9 có đáp án giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 9 Học kì 1. Mời các bạn cùng đón xem:
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 1)
Câu 1: 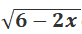
A.x ≥ 3
B.x > 3
C.x < 3
D.x ≤ 3
Câu 2: Kết quả của phép tính 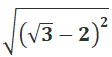
A.√3 - 2
B. 2 - √3
C. 1
D. Kết quả khác
Câu 3: 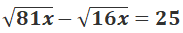
A. 25
B. 9
C. – 25
D. – 9
Câu 4: Hai đường thẳng y = ax + 2 và y = 4x + 5 song song với nhau khi :
A. a = - 4
B. a ≠ 4
C. a = 4
D. a ≠ -4
Câu 5: Hàm số y = (m - 3)x + 3 nghịch biến khi m nhận giá trị:
A.m > 3
B.m < 3
C.m ≥ 3
D.m ≤ 3
Câu 6: Cho tam giác BDC vuông tại D, ∠B = 60o , BD = 3 cm. Độ dài cạnh DC bằng:
A.3 cm
B.3√3 cm
C.√3 cm
D.12 cm
Câu 7: Đẳng thức nào sau đây là đúng:
A.sin 50o = cos 30o
B.tan 40o = cotg 60o
C.cotg 50o = tan 45o
D.sin 58o = cos 32o
Câu 8: Cho đoạn thẳng OI = 8 cm. Vẽ các đường tròn (O; 10cm); (I; 2cm). Hai đường tròn (O) và (I) có vị trí tương đối như thế nào với nhau?
A. (O) và (I) tiếp xúc trong với nhau
B. (O) và (I) tiếp xúc ngoài với nhau
C. (O) và (I) cắt nhau
D. (O) và (I) không cắt nhau
Phần tự luận (8 điểm)
Bài 1 (2,5 điểm) Cho biểu thức
a) Rút gọn P
b) Tính giá trị của P biết
c) Tìm m để có một giá trị x thỏa mãn :
P(√x - 2) + √x (m - 2x) - √x = m - 1
Bài 2 (2 điểm) Cho hàm số y =(m – 3)x + 2 có đồ thị là (d)
a) Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng – 3. Khi đó (d) tạo với trục Ox một góc nhọn hay góc tù. Vì sao?
b) Vẽ đồ thị với m tìm được ở câu a.
c) Tìm m để (d) cắt hai trục tọa độ tạo thành một tam giác có diện tích bằng 4.
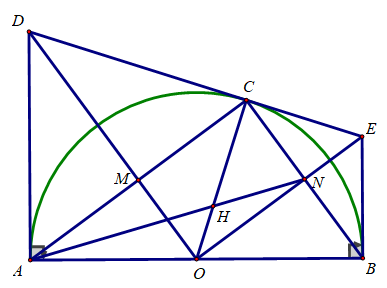
Bài 3 (3,5 điểm) Cho nửa đường tròn (O; R) đường kính AB cố định. Trên cùng một nửa mặt phẳng bờ AB chứa đường tròn, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Trên nửa đường tròn, lấy điểm C bất kì. Vẽ tiếp tuyến (O) tại C cắt Ax, By lần lượt tại D và E.
a) Chứng minh rằng AD + BE = DE
b) AC cắt DO tại M, BC cắt OE tại N. Tứ giác CMON là hình gì? Vì sao?
c) Chứng minh rằng OM.OD + ON.OE không đổi
d) AN cắt CO tại điểm H. Điểm H di chuyển trên đường nào khi C di chuyển trên nửa đường tròn (O; R).
Đáp án đề thi Học kì 1 môn Toán 9 - Đề số 1
Phần trắc nghiệm (2 điểm)
| 1.D | 2.B | 3.A | 4.C |
| 5.B | 6.B | 7.D | 8.A |
Phần tự luận (8 điểm)
Bài 1
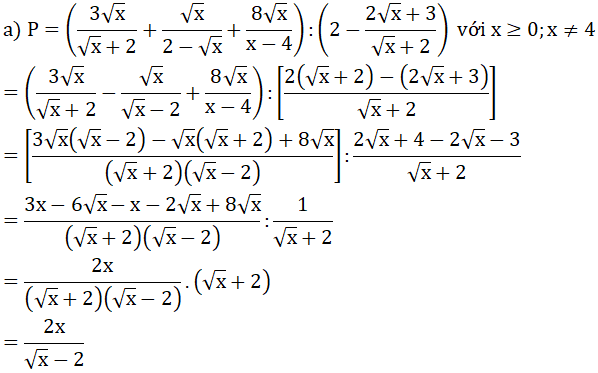
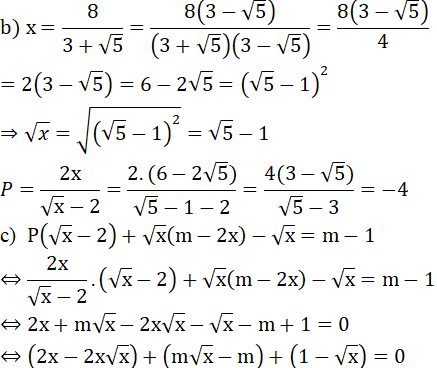
Để tồn tại 1 giá trị của x thỏa mãn đề bài thì: m = 2x + 1 phải thỏa mãn với x = 1
Thay x = 1 vào ta được: m = 2.1 + 1 = 3
Vậy m = 3 thỏa mãn đầu bài.
Bài 2 Cho hàm số y = (m – 3)x + 2 có đồ thị là (d)
a) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng – 3 khi:
0 = (m - 3).(-3) + 2 ⇔ 3m = 11 ⇔ m = 11/3
Khi đó (d) có phương trình là:
y = (11/3 - 3)x + 2 = 2/3 x + 2
Có hệ số a = 2/3 > 0
⇒ (d) tạo với trục Ox một góc nhọn
b) Tập xác định của hàm số R
Bảng giá trị
| x | 0 | - 3 |
| y = 2/3 x + 2 | 2 | 0 |
c) y = (m – 3)x + 2 (m ≠ 3)
Gọi A, B lần lượt là giao điểm của (d) và trục Ox, Oy và tam giác tạo thành là tam giác AOB vuông tại O
Bài 3
a) CE và EB là 2 tiếp tuyến cắt nhau tại E
⇒ EC = EB và CB ⊥ OE
Tương tự, DC và DA là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DA và AC ⊥ OD
Khi đó: AD + BE = DC + EC = DE
b) Xét tứ giác OMCN có:
∠(OMC) = 90o (AC ⊥ OD)
∠(ONC) = 90o (CB ⊥ OE)
∠(NCM) = 90o (AC ⊥ CB)
⇒ Tứ giác OMCN là hình chữ nhật
c) Xét tam giác DOC vuông tại C, CM là đường cao có:
OM.OD = OC2 = R2
Xét tam giác EOC vuông tại C, CN là đường cao có:
ON.OE = OC2 = R2
Khi đó: OM.OD + ON.OE = 2R2
Vậy OM.OD + ON.OE không đổi
d) Ta có: N là trung điểm của BC
⇒ AN là trung tuyến của ΔABC
CO cũng là trung tuyến của ΔABC
AN ∩ CO = H
⇒ H là trọng tâm ΔABC
Vậy khi C di chuyển trên nửa đường tròn (O) thì H di chuyển trên nửa đường tròn
(O; R/3)
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 2)
Bài 1: (1.5 điểm) Thực hiện các phép tính:
Bài 2: (1.5 điểm) Cho hàm số y = 2x + 3 có đồ thị (d1) và hàm số y = – x có đồ thị (d2).
a) Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (d1) và (d2) bằng phép toán.
Bài 3: (1.5 điểm) Cho biểu thức:
a) Thu gọn biểu thức A.
b) Tìm giá trị nhỏ nhất của A.
Bài 4: (2 điểm) Giải các phương trình:
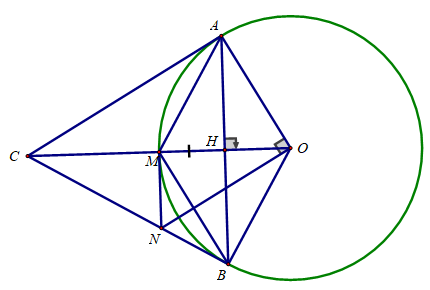
Bài 5: (3.5 điểm) Cho đường tròn (O;R) và điểm M thuộc đường tròn (O). Đường trung trực của đoạn thẳng OM cắt đường tròn (O) tại A và B và cắt OM tại H.
a) Chứng minh H là trung điểm của AB và tam giác OMA đều.
b) Chứng minh tứ giác OAMB là hình thoi.
c) Tiếp tuyến tại A của (O) cắt tia OM tại C. Chứng minh CB = CA.
d) Đường thẳng vuông góc với OA tại O cắt BC tại N. Chứng minh MN là tiếp tuyến của đường tròn (O).
Đáp án đề thi Học kì 1 môn Toán 9 - Đề số 2
Bài 1: (1.5 điểm)
= (√5 + 1)2 (3 - √5)
= (6 + 2√5)(3 - √5)
= 2(3 + √5) (3 - √5)
= 8
Bài 2: (1.5 điểm)
a) Tập xác định R
Bảng giá trị:
| x | 0 | -1 |
| y = 2x + 3 | 3 | 1 |
| x | 0 | -1 |
| y = - x | 0 | 1 |
Gọi (xo; yo ) là tọa độ giao điểm của d1 và d2
Khi đó ta có:
(yo = 2xo + 3 và yo = -xo
⇒ -xo = 2xo + 3 ⇔ 3xo = -3 ⇔ xo = -1
⇒ yo = -xo = 1
Vậy tọa độ giao điểm của d1 và d2 là (- 1; 1)
Bài 3: (1.5 điểm)
Vậy GTNN của biểu thức A là 0, đạt được khi x = 0
Bài 4: (2 điểm)
Bài 5: (3.5 điểm)
a) Chứng minh H là trung điểm của AB
Ta có OM vuông góc AB tại H (gt)
Vậy H là trung điểm của AB (đường kính vuông góc với một dây cung)
Chứng minh tam giác OAM đều:
Ta có: AM = AO (A là trung trực của OM)
và OA = OM = R
Suy ra AM = AO = OM
Vậy ΔOAM đều.
b) Chứng minh tứ giác OAMB là hình thoi.
Do H là trung điểm của AB (cmt)
H là trung điểm của OM
nên tứ giác OAMB là hình bình hành mà OM vuông góc AB.
Vậy tứ giác OAMB là hình thoi.
c) Xét ΔOAC và ΔOBC có:
OA = OB = R
∠(AOC) = ∠(BOC) (tính chất đường chéo hình thoi)
OC là cạnh chung
⇒ ΔOAC = ΔOBC (c.g.c)
⇒ AC = BC
d) Ta có: CA ⊥ OA (CA là tiếp tuyến của (O)
và ON ⊥ OA (gt)
⇒ CA // ON ⇒ ∠(CON) = ∠(ACO) (sole trong)
Mà ∠(ACO) = ∠(BCO) (ΔOAC = ΔOBC)
⇒ ∠(CON) = ∠(BCO) ⇒ ΔNCO cân tại N
Xét tam giác CAO vuông tại A có ∠(AOC) = 60o( ΔAMO đều) nên:
⇒ M là trung điểm của OC
ΔNCO cân tại N có NM là trung tuyến ⇒ NM cũng là đường cao
Hay NM là tiếp tuyến của (O)
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 3)
Phần trắc nghiệm (2 điểm)
Câu 1: 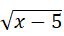
A.x > 5
B.x ≥ 5
C.x < 5
D.x ≤ 5
Câu 2: Biểu thức 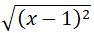
A.x - 1
B.1 - x
C.|x - 1|
D.(x - 1)2
Câu 3: Giá trị của biểu thức 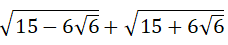
A.6
B.12√6
C.√30
D.3
Câu 4: Nếu đồ thị y = mx + 2 song song với đồ thị y = -2x + 1 thì:
A. Đồ thị hàm số y = mx + 2 cắt trục tung tại điểm có tung độ bằng 1
B. Đồ thị hàm số y = mx + 2 cắt trục hoành tại điểm có hoành độ bằng 2
C. Hàm số y = mx + 2 đồng biến
D. Hàm số y = mx + 2 nghịch biến
Câu 5: Đường thẳng 3x – 2y = 5 đi qua điểm:
A. (1; - 1)
B. (5; -5)
C. (1; 1)
D. (-5; 5)
Câu 6: Giá trị của biểu thức B = cos 62o -sin 28o là:
A. 2 cos 62o
B.0
C. 2 sin 28o
D. 0,5
Câu 7:Cho (O; 6cm) và đường thẳng a. Gọi d là khoảng cách từ tâm O đến a. Điều kiện để a cắt (O) là:
A. Khoảng cách d > 6cm
B. Khoảng cách d = 6 cm
C. Khoảng cách d ≥ 6cm
D. Khoảng cách d < 6 cm
Câu 8: Độ dài cạnh của tam giác đều nội tiếp đường tròn (O; R) bằng:
Phần tự luận (8 điểm)
Bài 1 (2.5 điểm) Cho biểu thức:
a) Rút gọn biểu thức P
b) Tính giá trị của biểu thức Q tại x = 9
c) Tìm các giá trị x để M = P. Q có giá trị âm.
Bài 2 (2 điểm) Cho đường thẳng d1:y = mx + 2m - 1 (với m là tham số) và d2: y = x + 1
a) Với m = 2. Hãy vẽ các đường thẳng d1 và d2 trên cùng một mặt phẳng tọa độ. Tìm tọa độ gia điểm của hai đường thẳng d1 và d2
b) Tìm giá trị của m để đường thẳng d1 cắt trục hoành tại điểm có hoành độ bằng – 3.
c) Chứng mình rằng đường thẳng d1 luôn đi qua một điểm cố định với mọi giá trị của m.
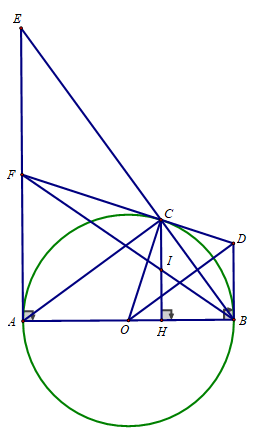
Bài 3 (3.5 điểm) Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)
a) Chứng minh tam giác ABC vuông. Tính độ dài CH và số đo ∠(BAC) (làm tròn đến độ)
b) Tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại D. Chứng minh OD ⊥ BC
c) Tiếp tuyến tại A của đường tròn (O) cắt BC tại E. Chứng minh:CE.CB = AH. AB
d) Gọi I là trung điểm của CH. Tia BI cắt AE tại F. Chứng minh: FC là tiếp tuyến của đường tròn (O).
Đáp án đề thi Học kì 2 môn Toán 9 - Đề số 3
Phần trắc nghiệm (2 điểm)
| 1.B | 2.C | 3.A | 4.D |
| 5.A | 6.B | 7.D | 8.C |
Phần tự luận (8 điểm)
Bài 1
a) Với x > 0; x ≠ 4,ta có:
Kết hợp với điều kiện thì các giá trị của x thỏa mãn là 0 < x < 9; x ≠ 4
Bài 2
Với m = 2 thì d1: y = 2x + 3; d2: y = x + 1
Tập xác định của hàm số R
Bảng giá trị
| x | 0 | - 1 |
| y = 2x + 3 | 3 | 1 |
| x | 0 | - 1 |
| y = x + 1 | 1 | 0 |
Gọi A (xo; yo) là tọa độ giao điểm của d1 và d2
Khi đó:
(yo = 2xo + 3 và yo = xo + 1
⇒ 2xo + 3 = xo + 1 ⇔ xo = -2
⇒ yo = xo + 1 = -2 + 1 = -1
Vậy tọa độ giao điểm của d1 và d2 là (-2; -1)
b) d1 cắt trục hoành tại điểm có hoành độ bằng – 3 khi:
0 = -3m + 2m - 1 ⇔ -m - 1 = 0 ⇔ m = -1
Vậy với m = -1 thì d1 cắt trục hoành tại điểm có hoành độ bằng – 3
c) Giả sử đường thẳng d1 luôn đi qua một điểm cố định (x1; y1 ) với mọi giá trị của m.
⇒ y1 = mx1 + 2m - 1 với mọi m
⇔ m(x1 + 2) - 1 - y1 = 0 với mọi m
Vậy điểm cố định mà d1 luôn đi qua với mọi giá trị của m là (-2; -1).
Bài 3
a) Tam giác ABC nội tiếp (O) có AB là đường kính
⇒ ∠(ACB) = 90o
Hay tam giác ABC vuông tại C
Tam giác ABC vuông tại C, CH là đường cao có:
b) DC và DB là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DB
Lại có: OC = OB = R
⇒ OD là đường trung trực của BC hay OD ⊥ BC
c) Xét tam giác ACB vuông tại C, CH là đường cao nên :
AH.AB = AC2
Xét tam giác ABE vuông tại A, AC là đường cao nên :
EC.BC = AC2
⇒ AH.AB = EC.BC
d) Xét tam giác ACB vuông tại C, CH là đường cao nên :
Xét tam giác ABE vuông tại A, AC là đường cao nên :
⇒ EA = 2 FA ⇒ F là trung điểm của EA
Tam giác CEA vuông tại C có CF là trung tuyến
⇒ FC = FA
⇒ ΔFCA cân tại F ⇒ ∠(FCA) = ∠(FAC)
Lại có ΔOCA cân tại O ⇒ ∠(OCA) = ∠(OAC)
⇒ ∠(FCA) + ∠(OCA) = ∠(FAC) + ∠(OAC)
⇔ ∠(FCO) = ∠(FAO) = 90o
Vậy FC ⊥ CO hay FC là tiếp tuyến của (O)
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 4)
Bài 1: (1.5 điểm) Thực hiện các phép tính:
a) 4√24 - 3√54 + 5√6 - √150
Bài 2: (1.5 điểm) Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau:
Xác định b để đường thẳng (d3 ) y = 2x + b cắt (d2 ) tại điểm có hoành độ và tung độ đối nhau.
Bài 3: (1.5 điểm) Giải phương trình:
Bài 4: (2 điểm) Cho biểu thức:
a) Thu gọn biểu thức M.
b) Tìm giá trị của x để M < – 1 .
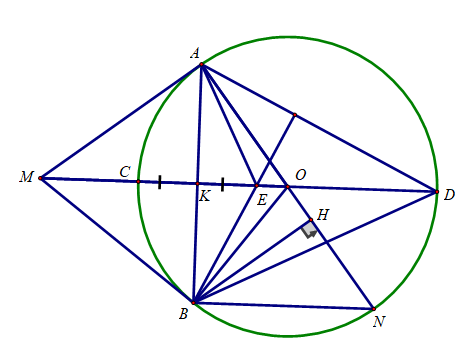
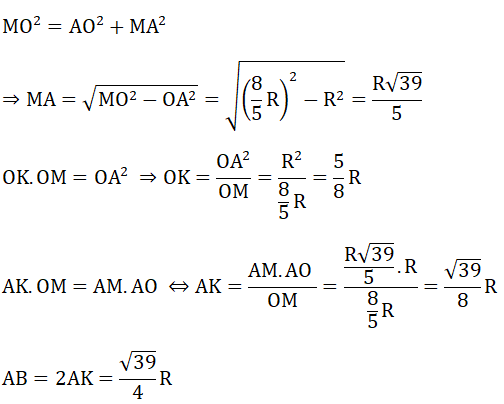
Bài 5: (3.5 điểm) Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
a) Chứng minh K là trung điểm của AB.
b) Tính MA, AB, OK theo R.
c) Kẻ đường kính AN của đường tròn (O). Kẻ BH vuông góc với AN tại H. Chứng minh MB.BN = BH.MO .
d) Đường thẳng MO cắt đường tròn (O) tại C và D (C nằm giữa O và M). Gọi E là điểm đối xứng của C qua K. Chứng minh E là trực tâm của tam giác ABD.
Đáp án đê fhti Học kì 1 môn Toán 9 - Đề số 4
Bài 1: (1.5 điểm)
a) 4√24 - 3√54 + 5√6 - √150
= 8√6 - 9√6 + 5√6 - 5√6
= -√6
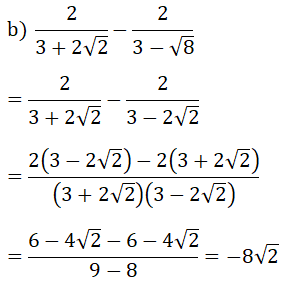
Bài 2: (1.5 điểm)
a) Tập xác định của hàm số R
Bảng giá trị
| x | 0 | 2 |
| y = -1/2 x | 0 | - 1 |
| y = 1/2 x + 3 | 3 | 4 |
b) Gọi A (m; - m) là tọa độ giao điểm của (d2 ) và (d3)
Khi đó:
-m = 1/2 m + 3 ⇔ 3/2 m = 3 ⇔ m = 2
Vậy tọa độ giao điểm của d2 và d3 là (2; -2)
⇒ -2 = 2.2 + b ⇔ b = -6
Vậy b = - 6
Bài 3: (1.5 điểm)
Vậy phương trình có nghiệm x = 0
Bài 4: (2 điểm)
a) Rút gọn M
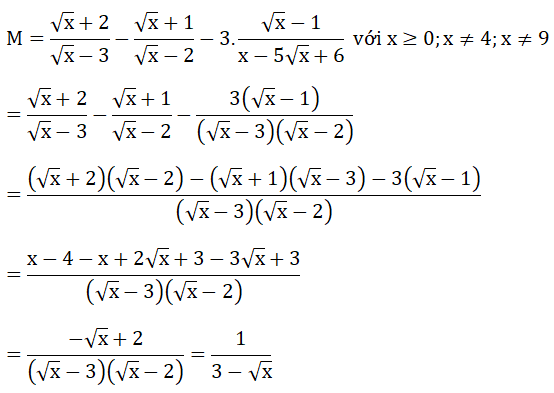
Bài 5: (3.5 điểm)
a) Ta có:
MA = MB ( tính chất 2 tiếp tuyến cắt nhau)
OA = OB ( cùng bằng bán kính đường tròn (O)
⇒ OM là đường trung trực của AB
OM ∩ AB = K ⇒ K là trung điểm của AB
b) Tam giác MAO vuông tại A, AK là đường cao có:
c) Ta có: ∠(ABN ) = 90o(B thuộc đường tròn đường kính AN)
⇒ BN // MO ( cùng vuông góc với AB)
Do đó:
∠(AOM) = ∠(ANB) (đồng vị))
∠(AOM) = ∠(BOM) (OM là phân giác ∠(AOB))
⇒ ∠(ANB) = ∠(BOM)
Xét ΔBHN và ΔMBO có:
∠(BHN) = ∠(MBO ) = 90o
∠(ANB) = ∠(BOM)
⇒ ΔBHN ∼ ΔMBO (g.g)
Hay MB. BN = BH. MO
d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 5)
Bài 1: (1.5 điểm) Thực hiện các phép tính:
a) (√75 - 3√2 - √12)(√3 + √2)
Bài 2: (1.5 điểm) Giải phương trình
Bài 3: (1.5 điểm) Cho hàm số y = –2x + 3 có đồ thị (d1) và hàm số y = x – 1 có đồ thị (d2)
a) Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ.
b) Xác định hệ số a và b biết đường thẳng (d3): y = ax + b song song với (d2) và cắt (d1) tại điểm nằm trên trục tung.
Bài 4: (2 điểm) Cho biểu thức :
a) Thu gọn biểu thức A.
b) Tìm x nguyên để A nguyên.
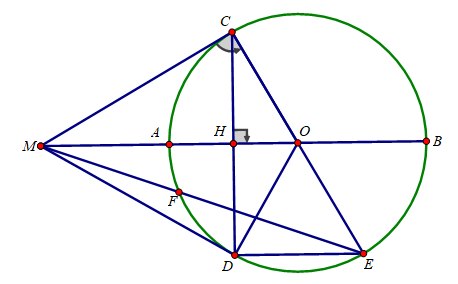
Bài 5: (3.5 điểm) Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.
a) Chứng minh MD là tiếp tuyến của đường tròn (O).
b) Kẻ đường kính CE của đường tròn (O). Tính MC, DE theo R.
c) Chứng minh HA2 + HB2 + CD2/2 = 4R2
d) ME cắt đường tròn (O) tại F (khác E). Chứng minh: ∠(MOF) = ∠(MEH )
Đáp án đề thi Học kì 1 môn Toán 9 - Đề số 5
Bài 1: (1.5 điểm)
a) (√75 - 3√2 - √12)(√3 + √2)
=(5√3 - 3√2 - 2√3)(√3 + √2)
=3(√3 - √2)(√3 + √2) = 3
Bài 2: (1.5 điểm)
⇔ x - 3 = 4
⇔ x = 7 (TM ĐKXĐ)
Vậy phương trình có nghiệm x = 7
Bài 3: (1.5 điểm)
a) Tập xác định của hàm số R
Bảng giá trị
| x | 0 | 1 |
| y = -2x + 3 | 3 | 1 |
| x | 0 | 1 |
| y = x – 1 | - 1 | 0 |
b) Do (d3 ) song song với đường thẳng (d2 ) nên (d3 ) có dạng: y = x + b (b ≠ -1)
(d1 ) cắt trục tung tại điểm (0; 3)
Do (d3 ) cắt (d1 ) tại điểm nằm trên trục tung nên ta có:
3 = 0 + b ⇔ b = 3
Vậy phương trình đường thẳng (d3 ) là y = x + 3
Bài 4: (2 điểm)
x + 2√x - 3 = x - √x + 3√x - 3 = √x (√x - 1) + 3(√x - 1) = (√x - 1)(√x + 3)
a) Với điểu kiện x ≥ 0; x ≠ 1 ta có:
b) Tìm x nguyên để A nguyên
⇔ √x + 3 ∈ Ư(11) ⇔ √x + 3 ∈ {-11; -1; 1; 11}
Do √x + 3 ≥ 3 nên √x + 3 = 11 ⇔ √x = 8 ⇔ x = 64
Vậy với x = 64 thì A nguyên
Bài 5: (3.5 điểm)
a) Xét tam giác COD cân tại O có OH là đường cao
⇒ OH cũng là tia phân giác ⇒ ∠(COM) = ∠(MOD)
Xét ΔMCO và ΔMOD có:
CO = OD
∠(COM) = ∠(MOD)
MO là cạnh chung
⇒ ΔMCO = ΔMOD (c.g.c)
⇒ ∠(MCO) = ∠(MDO)
∠(MCO) = 90o nên ∠(MDO) = 90o
⇒ MD là tiếp tuyến của (O)
b) Ta có: OM = OA + AM = R + R = 2R
Xét tam giác MCO vuông tại C, CH là đường cao có:
MO2 = MC2 + OC2
CH.OM = CM.CO
Lại có: CD = 2CH ⇒ CD = R√3
Tam giác CDE nội tiếp (O) có CE là đường kính nên ΔCDE vuông tại D
Theo định lí Py ta go ta có:
CE2 = CD2 + DE2
c) Ta có: ΔCOD cân tại O có OH là đường cao cũng là đường trung tuyến của tam giác
⇒ CH = HD = CD/2 ⇒ CH2 = DH2 = CD2 /4
Tam giác ACH vuông tại H có:
AH2 + CH2 = CA2 ⇒ AH2 + CD2/4 = CA2 (1)
Tam giác CHB vuông tại H có:
BH2 + CH2 = CB2 ⇒ BH2 + CD2/4 = CB2 (2)
Từ (1) và (2) ta có:
d) Ta có: ∠(CFE) = 90o (F thuộc đường tròn đường kính CE)
Lại có CF là đường cao nên MC2 = MF.ME
Tương tự, ta có: MC2 = MH.MO
⇒ ME.MF = MH.MO
⇒
Xét ΔMOF và ΔMEN có:
∠(FMO) chung
⇒ ΔMOF ∼ ΔMEN (c.g.c)
⇒ ∠(MOF) = ∠(MEH)
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 6)
Câu 1. (2,5 điểm)
Cho biểu thức 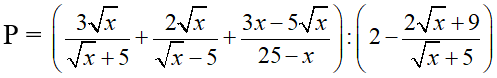
1) Rút gọn biểu thức P
2) Tính giá trị của biểu thức P khi ![]()
3) Tìm x để |P| = - P
Câu 2. (1,5 điểm) Giải các phương trình sau:
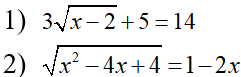
Câu 3. (2,0 điểm)
Cho hàm số y = (m2 + 1)x + 2m – 1 có đồ thị là đường thẳng dm.
1) Với m biết đường thẳng dm cắt trục tung tại điểm có tung độ là – 3
2) Với giá trị m tìm được ở câu trên, hãy vẽ đồ thị hàm số. Khi đó hãy tính khoảng cách từ gốc tọa độ đến đồ thị hàm số.
3) Tìm m biết đường thẳng dm song song với đường thẳng y = 2x + 1
Câu 4. (3,5 điểm)
Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm, kẻ AH vuông góc với BC (H ∈ BC). Vẽ đường tròn (O) đi qua điểm A và tiếp xúc với cạnh BC tại điểm B, đường tròn (I) đi qua điểm A và tiếp xúc với cạnh BC tại điểm C.
1) Tính độ dài của AH.
2) Chứng minh rằng: Các đường tròn (O) và (I) tiếp xúc ngoài với nhau tại A.
3) Gọi M là trung điểm của BC. Chứng minh rằng: Tam giác IMO vuông và OI là tiếp tuyến của đường tròn đường kinh BC.
Câu 5. (0,5 điểm)
Tìm giá trị lớn nhất, nhỏ nhất của biểu thức: 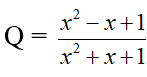
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 7)
Câu 1. (2,0 điểm) Rút gọn các biểu thức:
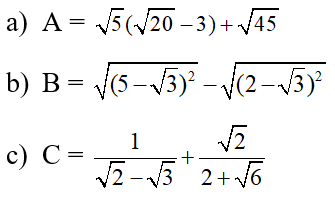
Câu 2. (2,0 điểm) Cho hai biểu thức:
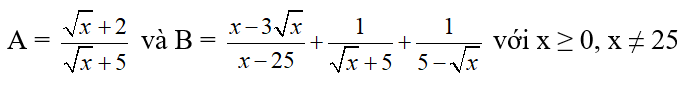
1. Tính giá trị của A tại x = 49
2. Chứng minh B = A
3. Tìm x để ![]()
Câu 3. (2,0 điểm) Cho hàm số y = mx + 5 (d) (với m là tham số khác 0)
a. Vẽ đồ thị hàm số (d) khi m = 2
b. Tìm m để (d) cắt đường thẳng y = - 3x + (m + 1) tại 1 điểm trên trục tung
c. Tìm m để (d) tạo với Ox một góc bằng 60°
Câu 4. (3,5 điểm)
Cho đường tròn (O; R) và một điểm H cố định nằm ngoài đường tròn. Qua H kẻ đường thẳng d vuông góc với đoạn thẳng OH. Từ 1 điểm S trên đường thẳng d kẻ hai tiếp tuyến SA, SB với đường tròn (O) (A, B là hai tiếp điểm). Gọi M, N lần lượt là giao điểm của đoạn thẳng SO với đoạn thẳng AB và đường tròn (O; R).
a) Chứng minh bốn điểm S, A, O, B cùng nằm trên 1 đường tròn
b) Chứng minh: OM.OS = R2
c) Chứng minh N là tâm đường tròn nội tiếp tam giác SAB
d) Khi S di chuyển trên đường thẳng d thì điểm M di chuyển trên đường nào?
Câu 5 (0,5 điểm) Cho x, y, z là các số dương. Chứng minh rằng: 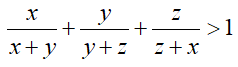
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 8)
Bài 1 (2,0 điểm) : Cho hai biểu thức 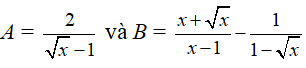
a) Tính giá trị của biểu thức A khi
b) Rút gọn biểu thức B
c) Tìm giá trị lớn nhất của biểu thức
Bài 2 (3,0 điểm) : Cho hàm số y = mx + 1 (1) (với m là tham số, m ≠ 0)
a) Tìm m để đồ thị hàm số (1) đi qua điểm M(-1; -1). Với m vừa tìm được, vẽ đồ thị hàm số (1) trên mặt phẳng tọa độ Oxy
b) Tìm m để đồ thị hàm số (1) song song với đường thẳng (d): y = (m2 – 2)x + 2m + 3.
c) Tìm m để khoảng cách từ gốc tọa độ O đến đồ thị hàm số (1) bằng
Bài 3 (4,0 điểm) : Cho đường tròn (O; R) cố định. Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB (A, B là các tiếp điểm). Gọi H là giao điểm của OM và AB.
a) Chứng minh OM vuông góc với AB và OH.OM = R2
b) Từ M kẻ cát tuyến MNP với đường tròn (N nằm giữa M và P), gọi I là trung điểm của NP (I khác O). Chứng minh 4 điểm A, M, O, I cùng thuộc một đường tròn và tìm tâm của đường tròn đó
c) Qua N kẻ tiếp tuyến với đường tròn (O), cắt MA và MB theo thứ tự ở C và D. Biết MA = 5cm, tính chu vi tam giác MCD.
d) Qua O kẻ đường thẳng d vuông góc với OM, cắt tia MA và MB lần lượt tại E và F. Xác định vị trí của M để diện tích tam giác MEF nhỏ nhất.
Bài 5 (0,5 điểm) :
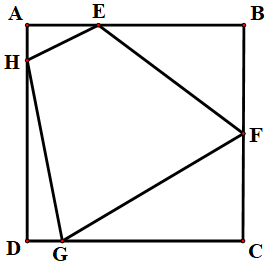
Cho một mảnh giấy hình vuông ABCD cạnh 6cm. Gọi E, F lần lượt là hai điểm nằm trên cạnh AB và BC sao cho AE = 2cm, BF = 3cm. Bạn Nam muốn cắt một hình thang EFGH (như hình bên) sao cho hình thang đó có diện tích nhỏ nhất. Xác định vị trí của H trên cạnh AD, để bạn Nam có thể thực hiện mong muốn của mình?
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 9)
Bài 1 (2,0 điểm) :
a) Rút gọn biểu thức:
b) Giải phương trình:
Bài 2 (2,0 điểm) : Cho hai biểu thức
a) Tính giá trị của biểu thức A khi x = 25
b) Rút gọn biểu thức B
c) Đặt P = A.B. Tìm giá trị nguyên của x để P < 1
Bài 3 (2,0 điểm) : Cho hàm số y = (2 – m)x + m + 1 (với là tham số và m khác 2) có đồ thị là đường thẳng (d).
a) Tìm m để đồ thị hàm số đi qua điểm A(-1;5); vẽ đồ thị hàm số với giá trị của m vừa tìm được
b) Tìm m để đường thẳng (d) cắt đường thẳng y = 3x – 1 tại điểm có hoành độ bằng 2, tìm tọa độ giao điểm.
Bài 4 (3,5 điểm) : Cho đường tròn (O;R) và một điểm A sao cho OA = 2R, vẽ các tiếp tuyến AB, AC với (O;R), B và C là các tiếp điểm. Vẽ đường kính BOD.
a) Chứng minh 4 điểm A, B, O, C cùng thuộc một đường tròn
b) Chứng minh rằng: DC // OA
c) Đường trung trực của BD cắt AC và CD lần lượt tại S và E. Chứng minh rằng OCEA là hình thang cân.
d) Gọi I là giao điểm của đoạn OA và (O), K là giao điểm của tia SI và AB. Tính theo R diện tích tứ giác AKOS
Bài 5 (0,5 điểm) : Giải phương trình:
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 10)
Bài 1 (2,0 điểm) : Cho biểu thức
1) Tính giá trị của biểu thức A khi x = 16
2) Rút gọn biểu thức 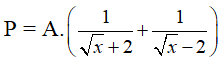
3) Tìm các giá trị của x để
Bài 2 (2,0 điểm) :
1) Thực hiện phép tính:
2) Giải các phương trình sau:
Bài 3 (2,0 điểm) : Cho hàm số y = (m – 1)x + 3 có đồ thị là đường thẳng (d)
1) Vẽ đường thẳng (d) khi m = 2
2) Tìm m để đường thẳng (d) song song với đường thẳng y = 2x + 1
3) Tính khoảng cách từ gốc tọa độ đến đường thẳng được vẽ ở câu 1
Bài 4 (3,5 điểm) : Cho điểm E thuộc nửa đường tròn tâm O, đường kính MN. Kẻ tiếp tuyến tại N của nửa đường tròn tâm O, tiếp tuyến này cắt đường thẳng ME tại D.
1) Chứng minh rằng: ΔMEN vuông tại E. Từ đó chứng minh DE.DM = DN2
2) Từ O kẻ OI vuông góc với ME (I ∈ ME).
Chứng minh rẳng: 4 điểm O; I; D; N cùng thuộc một đường tròn.
3) Vẽ đường tròn đường kính OD, cắt nửa đường tròn tâm O tại điểm thứ hai là A. Chứng minh rằng: DA là tiếp tuyến của nửa đường tròn tâm O.
4) Chứng minh rằng:
Bài 5 (0,5 điểm) : Cho x, y là các số dương và
Tìm giá trị nhỏ nhất của biểu thức P = x + y
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 11)
Bài 1 (1 điểm): Thực hiện phép tính
a) 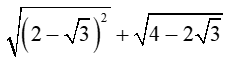
b) 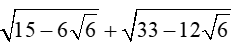
Bài 2 (1 điểm): Tìm x
a) 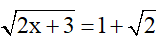
b) 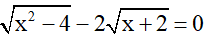
Bài 3 (2 điểm): Cho đường thẳng (d): y = 2x + m + 1.
a) Tìm m để (d) đi qua điểm C(1; 5)
b) Tìm m để đường thẳng d: y = 2x + m + 1 cắt hai trục Ox, Oy tại hai điểm A và B sao cho OA = OB.
Bài 4 (2 điểm): Cho biểu thức: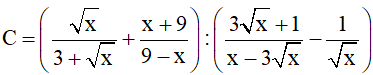 với x > 0; x ≠ 9.
với x > 0; x ≠ 9.
a) Rút gọn C
b) Tìm x sao cho C < -1.
Bài 5 (3,5 điểm): Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM =R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
a) Chứng minh K là trung điểm của AB.
b) Tính MA, AB, OK theo R.
c) Kẻ đường kính AN của đường tròn (O). Kẻ BH vuông góc với AN tại H. Chứng minh MB.BN = BH.MO.
d) Đường thẳng MO cắt đường tròn (O) tại C và D (C nằm giữa O và M). Gọi E là điểm đối xứng của C qua K. Chứng minh E là trực tâm của tam giác ABD.
Bài 6 (0,5 điểm): Giải phương trình sau:
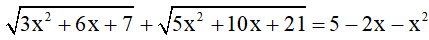
Đáp án đề thi Học kì 1 môn Toán 9 - Đề số 11
Bài 1:
a) 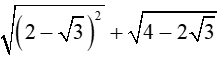
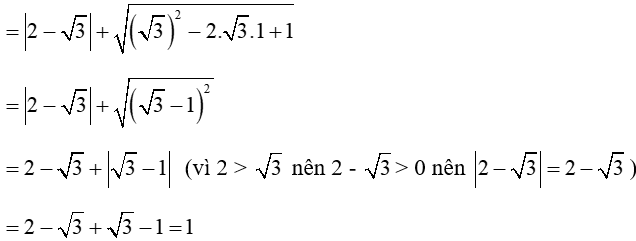
b) 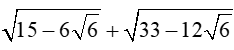
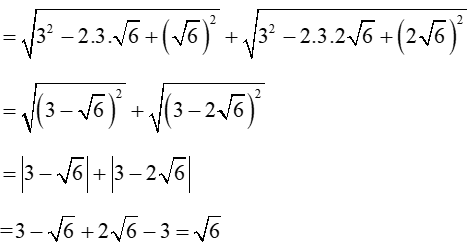
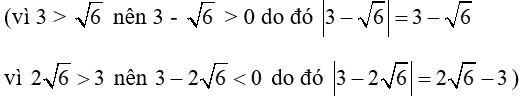
Bài 2:
a) Điều kiện: 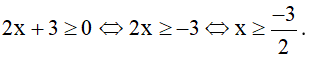
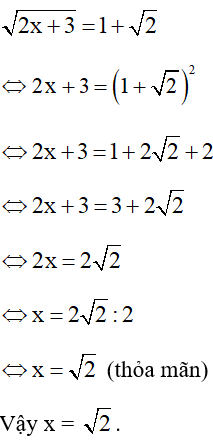
b) Điều kiện
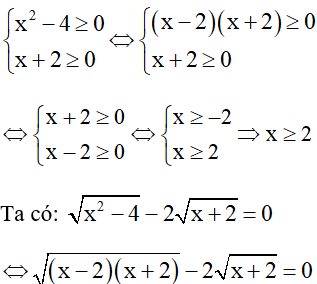
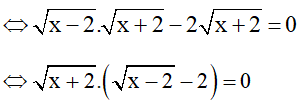
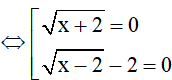
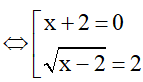
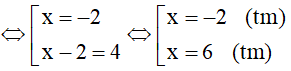
Vậy x = -2 và x = 6
Bài 3:
a) Để (d): y = 2x + m + 1 đi qua C (1; 5) ta thay x = 1; y = 5 vào hàm số ta có:
5 = 2.1 + m + 1
<=> 5 = m + 3
<=> m = 5 - 3
<=> m = 2
Vậy m = 2 thì (d) đi qua điểm C(1; 5).
b) Cho x = 0 => y = m + 1 => B(0; m +1 ) thuộc Oy
Cho y = 0 => 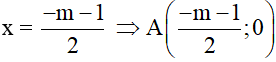 thuộc Ox
thuộc Ox
OB = |m +1 |
OA = 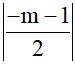
Ta có:
OA = OB
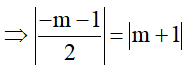
TH1: 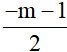 = m+1
= m+1
⇔ -m -1 = 2m +2
⇔ 3m = -3
⇔ m = -1
TH2: 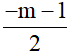 = -m -1
= -m -1
⇔ -m -1 = 2m -2
⇔ m = -1
Vậy m = -1 thì OA = OB
Bài 4:
a) 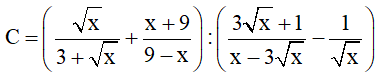
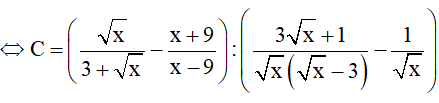
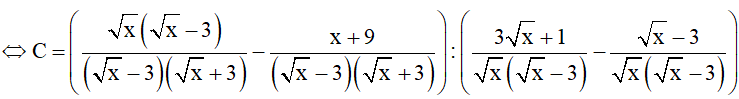
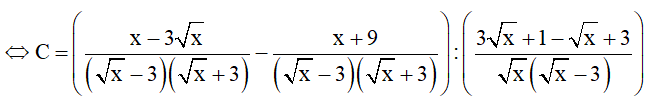
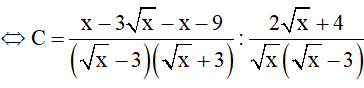
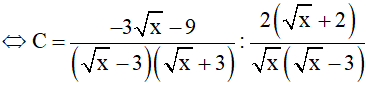
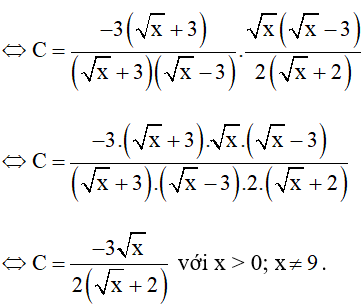
b) 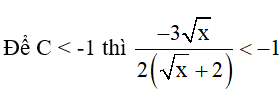
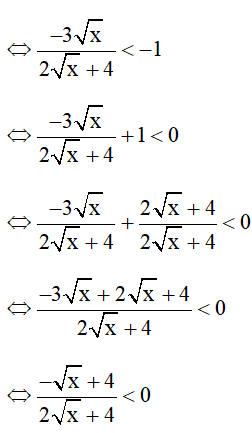
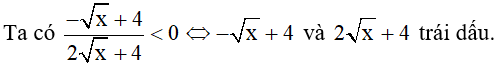
Ta có: 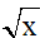 ≥ 0 với mọi x thỏa mãn điều kiện
≥ 0 với mọi x thỏa mãn điều kiện
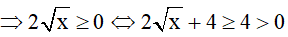
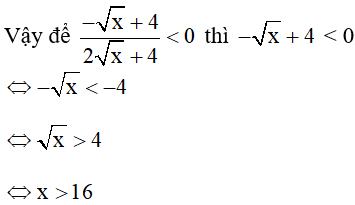
Kết hợp với điều kiện đề bài ta có: 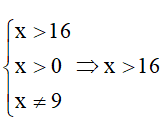
Vậy x > 16 thì C < -1
Bài 5:
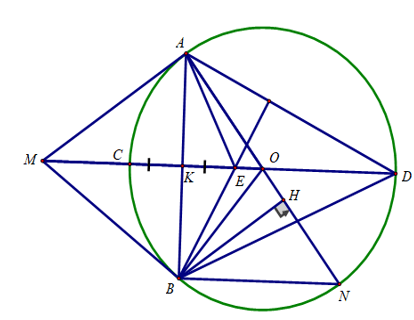
a) Ta có:
MA = MB (tính chất 2 tiếp tuyến cắt nhau) nên M nằm trên đường trung trực của AB
OA = OB (cùng bằng bán kính đường tròn (O) nên O nằm trên đường trung trực của AB
Do đó, OM là đường trung trực của AB
OM ∩ AB = K ⇒ K là trung điểm của AB
b) Tam giác MAO vuông tại A, AK là đường cao có:
MO² =AO² +MA²
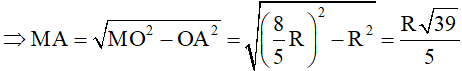
AK.OM = AM.AO
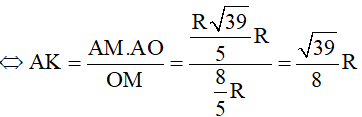
Mà AB = 2AK nên AB = 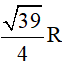
c) Ta có:
∠ABN = 90° (B thuộc đường tròn đường kính AN)
=> BN // MO (do BN và MO cùng vuông góc với AB)
Do đó:
∠AOM = ∠ANB (hai góc đồng vị)
Mà ∠AOM = ∠BOM (OM là phân giác ∠AOB)
Nên ⇒ ∠ANB = ∠BOM
Xét tam giác BHN và tam giác MBO có:
∠BHN = ∠MBO = 90°
∠ANB = ∠BOM
Do đó: ΔBHN ∼ ΔMBO (g.g)
=>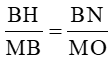
Hay MB.BN = BH.MO
d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB
Bài 6:
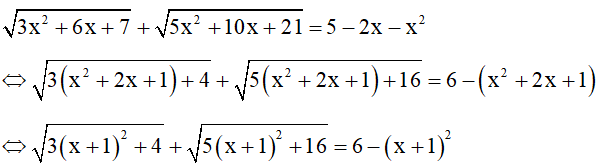
Ta có:
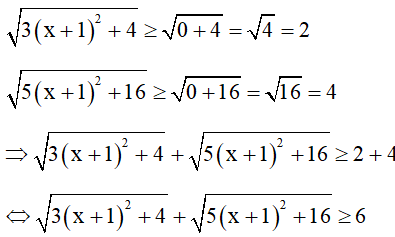
Lại có:
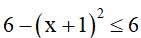
Dấu bằng xảy ra để vế trái bằng vế phải là
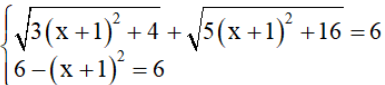
⇒( x+1)² = 0
⇔ x + 1 = 0
⇔ x = -1
Vậy nghiệm của phương trình là S = { -1}
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 12)
Câu 1 (2,0 điểm):
1) Thực hiện phép tính
a) 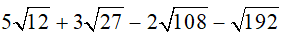
b) 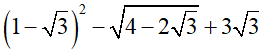
2) Giải phương trình 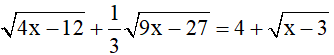
Câu 2 (2,0 điểm):
Với x> 0; x ≠ 9 cho các biểu thức 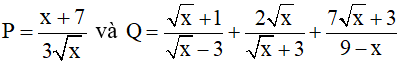
1) Tính giá trị của biểu thức P khi x = 4
2) Chứng minh 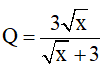
3) Tìm giá trị nhỏ nhất của biểu thức A=P.Q
Câu 3 (2,0 điểm):
1) Cho hàm số bậc nhất y= (m+3)x + 3m-1 có đồ thị(d) (m là tham số; m ≠ -3)
a) Vẽ (d) khi m=0
b) Tìm m để đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 5.
c) Xác định m để đường thẳng (d) trùng với đườn thẳng y = 2x – 4.
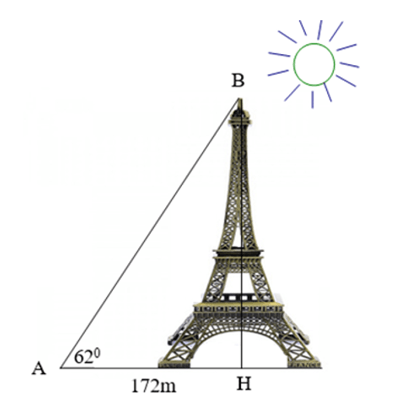
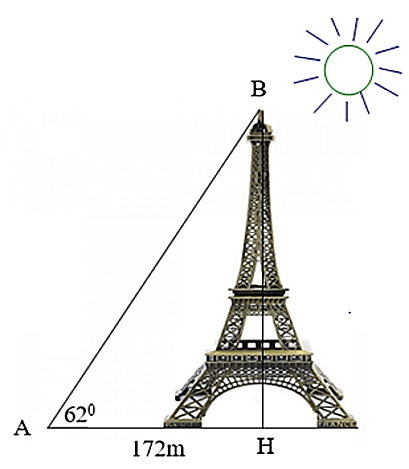
2) Hãy tính chiều cao tháp Eiffel mà không cần lên đỉnh tháp biết góc tạo bởi tia nắng mặt trời và mặt đất là và bóng của cái tháp trên mặt đất là 172m.
(làm tròn đến chữ số thập phân thứ nhất).
Câu 4 (3,5 điểm): Cho nửa đường tròn (O) đường kính AB (). Trên nửa mặt phẳng bờ AB chứa nửa đường tròn kẻ hai tia tiếp tuyến Ax, By của nửa đường tròn. Lấy điểm C bất kì thuộc nửa đường tròn ( C khác A và B), qua C kẻ tiếp tuyến của nửa đường tròn cắt Ax, By thứ tự tại M và N.
a) Chứng minh bốn điểm cùng thuộc một đường tròn.
b) Nối điểm O với điểm M, điểm O với điểm N. Chứng minh AM.BN = R2
c) Đoạn ON cắt nửa đường tròn (O) tại I. Chứng minh I là tâm đường tròn nội tiếp tam giác CNB
d) Cho Ab= 6cm. Xác định vị trí của M và N để hình thang AMNB có chu vi bằng 18 cm
Câu 5. (0,5 điểm): 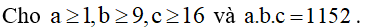 .
.
Tìm giá trị lớn nhất của biểu thức 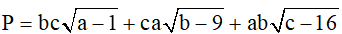
Đáp án đề thi Học kì 1 môn Toán 9 - Đề số 12
Câu 1 (2,0 điểm):
1) Thực hiện phép tính
a) 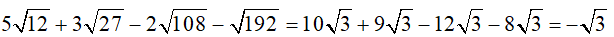
b) 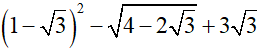
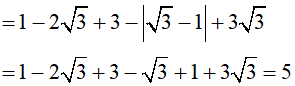
2) Giải phương trình
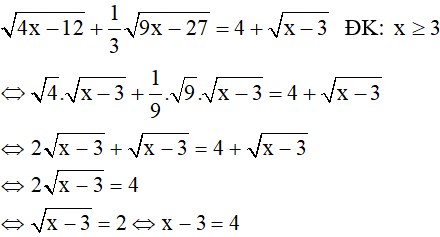
⇔ x = 7 (thỏa mãn điều kiện x ≥ 3 )
Vậy phương trình có tập nghiệm S ={ 7 }
Câu 2 (2,0 điểm):
Với x > 0, x ≠ 9 cho các biểu thức 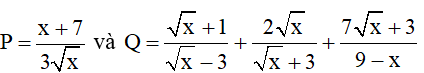
1) Tính giá trị của biểu thức P khi x= 4
x= 4 thỏa mãn điều kiện x > 0, x ≠ 9. Thay x= 4 vào biểu thức P ta có:
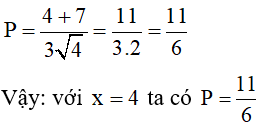
2) Chứng minh 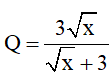
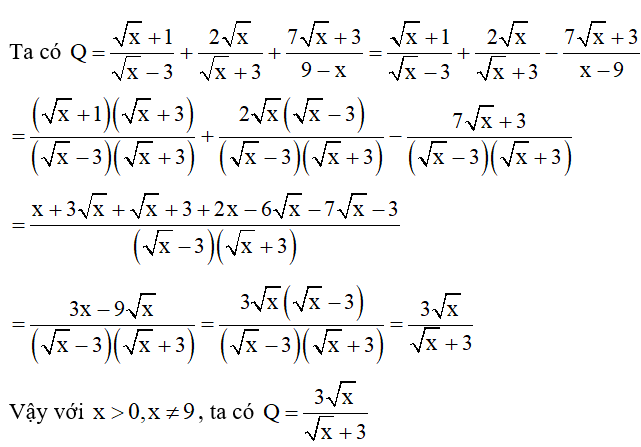
3) Tìm giá trị nhỏ nhất của biểu thức
Với x > 0, x ≠ 9, ta có
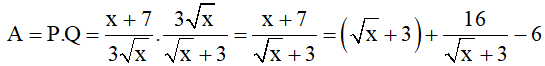
Áp dụng bất đẳng thức Cosi cho hai số không âm ta có:
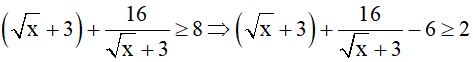
Dấu " = " xảy ra ( thỏa mãn điều kiện x > 0, x ≠ 9)
Vậy giá trị nhỏ nhất của biểu thức A = 2 tại x = 1
Câu 3 (2,0 điểm):
1) Cho hàm số bậc nhất y= (m+3)x + 3m-1 có đồ thị (d) (m là tham số; m ≠ -3)
a) Vẽ (d) khi m = 0
Khi m = 0 ta có công thức y= 3x - 1
Bảng giá trị tương ứng của x và y
|
x |
0 |
|
|
y = 3x – 1 |
-1 |
0 |
Đồ thị hàm số y = 3x – 1 là đường thẳng đi qua 2 điểm (0; -1) và 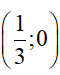
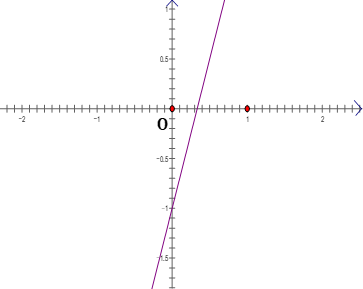
b) Tìm m để đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 5
Đường thẳng cắt trục tung tại điểm có tung độ bằng 5. Thay x = 0 và y = 5 vào hàm số ta được:
5 = (m + 3).0 + 3m – 1
⇔ 3m - 1 = 5 ⇔ 3m = 6 ⇔ m = 2
c) Xác định m để đường thẳng (d) trùng với đường thẳng y = 2x – 4
Đường thẳng (d) trùng với đường thẳng y = 2x – 4 , ta có:
a = a’ và b = b’
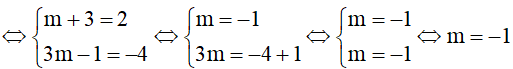 ( thỏa mãn điều kiện m ≠ -3)
( thỏa mãn điều kiện m ≠ -3)
Vậy m = -1 thì đường thẳng trùng với đường thẳng y = 2x – 4 .
2) Giả sử chiều cao của tháp, bóng của tháp và tia nắng mặt trời tạo thành tam giác ABH vuông tại H như hình.
Chiều dài của tháp Eiffel là độ dài đoạn BH.
Xét tam giác ABH vuông tại H ta có:
BH = AH.tan∠BAH
(tỉ số lượng giác)
⇒ BH = 172.tan62° ≈ 323,5m
Vậy chiều cao của tháp Eiffel là 323,5m.
Câu 4 (3,5 điểm):
a) MA là tiếp tuyến của nửa đường tròn (O) tại A (gt)
⇒MA ⊥ OA(tính chất tiếp tuyến)
⇒∠OAM =90° ⇒ tam giác OAM vuông tại A (định nghĩa)
⇒ Ba điểm O, A, M thuộc đường tròn đường kính OM (1)
MC là tiếp tuyến của nửa đường tròn (O) tại C (gt)
⇒MC ⊥ OC(tính chất tiếp tuyến)
⇒∠OCM =90°⇒tam giác OCM vuông tại C (định nghĩa)
=> Ba điểm O, A, M thuộc đường tròn đường kính OM (2)
Từ (1) và (2) suy ra bốn điểm cùng thuộc đường tròn đường kính OM
b) Nối điểm O với điểm M, điểm O với điểm N. Chứng minh AM.BN = R²
MA, MC là hai tiếp tuyến của nửa đường tròn (O) lần lượt tại A và C (gt)
⇒ MA = MC (3)
và OM là tia phân giác của ∠AOC (tính chất hai tiếp tuyến cắt nhau)
Chứng minh tương tự có NC = NB (4)
và ON là tia phân giác của ∠BOC
Mà ∠AOCvà ∠BOC là hai góc kề bù ⇒ OM ⊥ ON ⇒ tam giác OMN vuông tại O
MC là tiếp tuyến của nửa đường tròn (O) tại C (gt)
⇒ OC ⊥ MC ( tính chất tiếp tuyến ) OC ⊥ MN
⇒ OM là đường cao của tam giác OMN
Xét tam giác OMN vuông tại O, có OC là đường cao
⇒ OC² = MC.NC (5)
Từ (3), (4), (5) suy ra OC² = AM.BN
Mà OC = R suy ra AM.BN = R²
c) Đoạn ON cắt nửa đường tròn (O) tại I. Chứng minh I là tâm đường tròn nội tiếp tam giác CNB
Gọi giao điểm của CB và ON là H
NC, NB là hai tiếp tuyến của nửa đường tròn (O) lần lượt tại C và B (gt)
⇒ NO là tia phân giác của ∠CNB (tính chất hai tiếp tuyến cắt nhau)
⇒ NH là tia phân giác của ∠CNB
Nửa đường tròn (O) có OC = OI (cùng là bán kính)
⇒ tam giác OCI cân tại O (định nghĩa) ⇒ ∠OCI=∠OIC (tính chất tam giác cân) (6)
Có OC ⊥ MC (chứng minh trên) ∠OCN = 90°
Mà ∠OCN = ∠OCI + ∠NCI ⇒ ∠OCI + ∠NCI = 90° (7)
Mặt khác NC = NB (chứng minh trên) ⇒ tam giác NCB cân tại N (định nghĩa)
Mà NH là tia phân giác của (chứng minh trên)
Suy ra NH là đường cao ứng với cạnh CB (tính chất tam giác cân) ⇒ NH ⊥ CB
⇒ tam giác HIC vuông tại H
∠HIC + ∠ICH = 90° ⇒ ∠OIC + ∠ICH = 90° (8)
Từ (6), (7), (8) ⇒ ∠ICH = ∠NCI
Mà tia CI nằm giữa hai tia CN và CH ⇒ CI là tia phân giác của ∠NCB
Tam giác CNB có hai đường phân giác NH và CI cắt nhau tại I
Suy ra I là tâm đường tròn nội tiếp tam giác CNB (đpcm)
d) Cho . Xác định vị trí của M, N để hình thang AMNB có chu vi bằng 18cm
Ax, By là hai tiếp tuyến của nửa đường tròn (O) tại A và B (gt)
=> Ax ⊥ AB và By ⊥ AB (tính chất tiếp tuyến)
=> Ax // By (từ vuông góc đến song song)
=> AM // BN
Tứ giác AMNB có AM // BN ⇒ Tứ giác AMNB là hình thang (định nghĩa)
Chu vi hình thang AMNB bằng
AM + MN + NB + AB = AM + MC + NC + NB + AB
= AM + AM + NB + NB + AB = AB +2( MA + NB )
Đặt MA = a, NB = b ( a > 0, b > 0)
⇒ 6+2(a+b) = 18 ⇔ a+b = 6 (9)
Nửa đường tròn (O) có AB = 6cm ⇒ OA = OB = 3cm ⇒ R = 3cm
Mà AM.BN = R² ⇒ AM.Bn = 9 ⇔ ab = 9 (10)
Từ (9) và (10) ⇒a²- 6a + 9 = 0 ⇔ (a - 3)² = 0 ⇔ a = 3
Suy ra b = 3
Vậy điểm M nằm trên tia Ax, điểm M cách điểm A một khoảng là 3cm
Điểm N nằm trên tia By, điểm N cách điểm B một khoảng là 3cm
Câu 5: (0,5 điểm)
Với . Áp dụng bất đẳng thức Cosi có
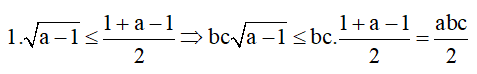
Chứng minh tương tự ta có:
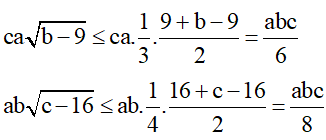
Suy ra:
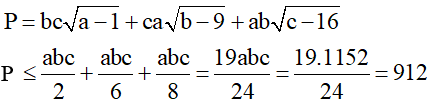
Dấu " = " xảy ra khi a= 2, b= 18, c= 32
Vậy P đạt giá trị lớn nhất là 912 khi a= 2, b= 18, c= 32
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 13)
Câu 1 (3điểm):
a) Tính giá trị của biểu thức A và B:
A = 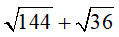
B=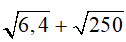
b) Rút gọn biểu thức :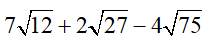
c) Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của
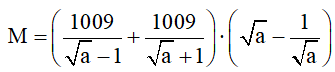 với a> 0; a ≠ 1
với a> 0; a ≠ 1
Câu 2 (2,0 điểm): Cho hàm số y = ax - 2 có đồ thị là đường thẳng
a) Biết đồ thị hàm số qua điểm A(1;0). Tìm hệ số a, hàm số đã cho là đồng biến hay nghịch biến trên R? Vì sao?
b) Vẽ đồ thị hàm số vừa tìm được.
c) Với giá trị nào của m để đường thẳng : y = (m - 1)x + 3 song song d1?
Câu 3 (2,0điểm): Cho tam giác ABC, đường cao AH, biết AB = 30cm, AC = 40cm, BC = 50cm.
a) Chứng minh tam giác ABC vuông tại A
b) Tính đường cao AH?
c) Tính diện tích tam giác AHC?
Câu 4 (2,5 điểm): Cho đường tròn (O; 6cm), điểm A nằm bên ngoài đường tròn,
OA = 12cm. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh BC vuông góc với OA.
b) Kẻ đường kính BD, chứng minh OA // CD.
c) Gọi K là giao điểm của AO với BC. Tính tích: OK.OA và số đo góc ∠BAO.
Câu 5 (0,5điểm): Tìm giá trị nhỏ nhất của biểu thức 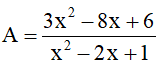
Đáp án đề thi Học kì 1 môn Toán 9 - Đề số 13
Câu 1 (3 điểm):
a) 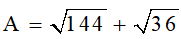
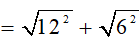
= 12 + 6 = 18
B = 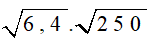
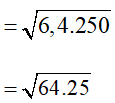
= 8.5 = 40
b, 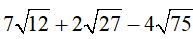
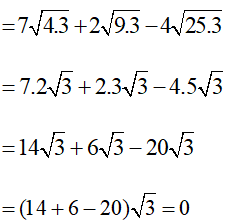
c) 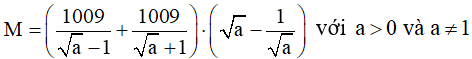
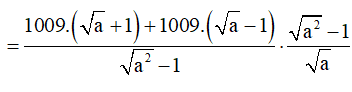
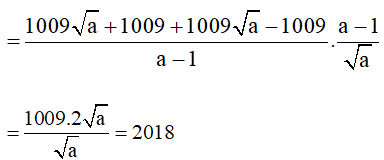
Vậy M không phụ thuộc vào A
Câu 2 (2 điểm):
a) Đồ thị hàm số y = ax – 2 qua điểm A(1; 0), thay x = 1; y = 0 vào hàm số ta có: 0 = a.1 – 2
=> a= 2
Vậy hàm số đó là y = 2x – 2
Hàm số đồng biến trên R, vì a = 2 > 0
b) Bảng giá trị tương ứng
|
x |
0 |
1 |
|
y = 2x - 2 |
-2 |
0 |
Vẽ đồ thị:
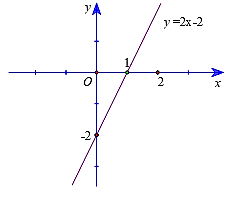 D
D
c) Để đường thẳng d2 // d1 thì 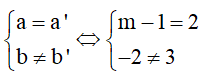 => m – 1 = 2
=> m – 1 = 2
<=> m = 3
Vậy m = 3 thì d2 // d1
Câu 3 (2 điểm):
a) Ta có: BC2 = 502 = 2500
AB2+AC2= 900+1600=2500
=> BC2 = AB2 + AC2
Do đó tam giác ABC vuông tại A (định lý Py – ta – go đảo)
b) Ta có: BC.AH = AB.AC (Hệ thức lượng trong tam giác vuông)
50.AH = 30.40
=> AH = 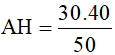 24 (cm)
24 (cm)
c) Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có :
AC2 = BC.HC => HC =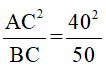 = 32(cm)
= 32(cm)
* 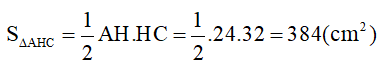
Câu 4 (2,5 điểm):
|
GT |
(O; 6cm); A ∉ O OA = 12cm, AB, AC là tiếp tuyến (B; C là tiếp điểm) BD = 2R, D ∈ D |
|
KL |
a) BC ⊥ OA b) OA // CD c) OK.OA = ? ∠BAO = ? |
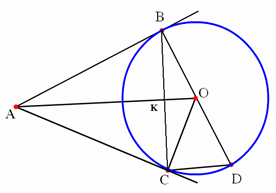
a) Vì AB và AC là hai tiếp tuyến cắt nhau nên ta có:
AB = AC (tính chất)
AO là phân giác ∠BAC(tính chất)
OA là phân giác ∠BOC(tính chất)
Xét tam giác ABC có: AB = AC (chứng minh trên)
Do đó, tam giác ABC cân tại A
mà AO là tia phân giác ∠BAC do đó AO là đường cao của tam giác ABC (tính chất)
=> AO ⊥ BC.
b) Vì B, C, D thuộc đường tròn (O) và BD là đường kính nên tam giác BCD vuông tại C. Do đó BC vuông góc với CD.
Mặt khác AO vuông góc với BC (chứng minh ở câu a)
Do đó AO // BC (quan hệ từ vuông góc đến song song)
c) Xét tam giác AOB vuông tại B đường cao BK
OK.OA = OBR(hệ thức lượng trong tam giác vuông)
⇔ OK.OA = R² = 6² = 36
Ta có: 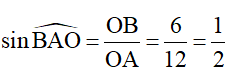
⇒ ∠BAO = 30°
Câu 5 (0,5 điểm):
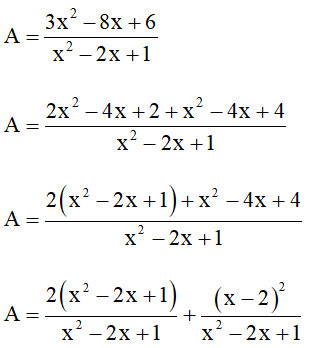
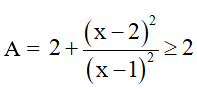
Biểu thức A đạt giá nhỏ nhất là 2 khi và chỉ khi 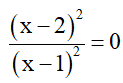
Hay x – 2 = 0 suy ra x = 2
Vậy Amin = 2 khi x = 2
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 14)
I. Trắc nghiệm
Câu 1: Căn bậc hai của 9 là:
A) 81
B) ±81
C) 3
D) ±3
Câu 2: Phương trình 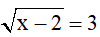 có nghiệm là:
có nghiệm là:
A) 9
B) ±9
C) ±4
D) 11
Câu 3: Điều kiện xác định của 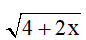 là:
là:
A) x ≥ 0
B) x ≥ 2
C) x ≥ -2
D) x ≤ 2
Câu 4: Kết quả của phép khai phương 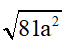 (với a < 0) là:
(với a < 0) là:
A) -9a
B) 9a
C) -9|a|
D) 81a
Câu 5: Tìm x biết 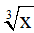 = -5:
= -5:
A) x = -25
B) x = -125
C) x = -512
D) x = 15
Câu 6: Rút gọn biểu thức 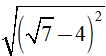 ta được kết quả cuối cùng là:
ta được kết quả cuối cùng là:
A) 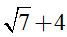
B) 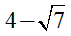
C) 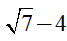
D) 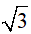
Câu 7: Trong hệ tọa độ Oxy, đường thẳng y = 2 - x song song với đường thẳng:
A) y = -x
B) y = -x + 3
C) y = -1 – x
D) Cả ba đường thẳng trên
Câu 8: Trong các hàm số bậc nhất sau, hàm số nào là hàm số nghịch biến:
A) y = 1 – 3x
B) y = 5x – 1
C) 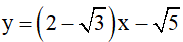
D) 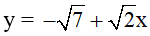
Câu 9: Nếu điểm B(1 ;-2) thuộc đường thẳng y = x – b thì b bằng:
A) -3
B) -1
C) 3
D) 1
Câu10: Cho hai đường thẳng: (d) : y = 2x + m – 2 và (d’) : y = kx + 4 – m; (d) và (d’) trùng nhau nếu :
A) k = 2 và m = 3
B) k = -1 và m = 3
C) k = -2 và m = 3
D) k = 2 và m = -3
Câu 11: Góc tạo bởi đường thẳng y = x + 1 và trục Ox có số đo là:
A) 450
B) 300
C) 600
D) 1350.
Câu 12: Hệ số góc của đường thẳng: y = -4x + 9 là:
A) 4
B) -4x
C) -4
D) 9
Câu13: Cho tam giác vuông cân ABC đỉnh A có BC = 6cm, khi đó AB bằng
A)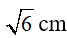
B)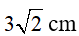
C) 36 cm
D)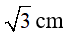
Câu 14: Cho 1 tam giác vuông có hai góc nhọn là và . Biểu thức nào sau đây không đúng:
A) sin α= cosβ
B) cotα= tanβ
C) sin2 α + cos2β = 1
D) tanα = cotβ
Câu 15: Cho tam giác ABC vuông ở A có AC = 3 cm , BC = 5cm. Giá trị của cotB là:
A) 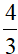
B) 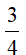
C) 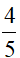
D) 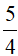
Câu 16: Cho tam giác ABC vuông tại A có AB = 9 cm, AC = 12 cm, BC = 15 cm. Tính độ dài AH là :
A) 8,4 cm
B) 7,2 cm
C) 6,8 cm
D) 4.2 cm
Câu 17: Tâm của đường tròn ngoại tiếp tam giác là giao điểm của các đường :
A) Trung tuyến
B) Phân giác
C) Đường cao
D) Trung trực
Câu 18: Hai đường tròn (O) và (O’) tiếp xúc ngoài. Số tiếp tuyến chung của chúng là:
A) 1
B) 2
C) 3
D) 4
Câu 19: Cho (O; 6cm) và đường thẳng a có khoảng cách đến O là d, điều kiện để đường thẳng a là cát tuyến của đường tròn (O) là:
A) d < 6cm
B) d = 6cm
C) d > 6cm
D) d 6cm
Câu 20: Dây AB của đường tròn (O; 5cm) có độ dài là 6cm. Khoảng cách từ O đến AB bằng:
A) 6cm
B) 7 cm
C) 4 cm
D) 5 cm
II. Tự luận(5 điểm)
Câu 1 (1 điểm): Tính:
a) 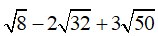
b) 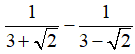
Câu 2 (1 điểm): Cho biểu thức: 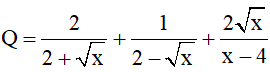
a) Rút gọn biểu thức Q
b) Tìm x để Q = 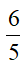 .
.
Câu 3 (1 điểm): Cho hàm số y = (m + 1)x – 3 (m ≠ -1)
Xác định m để :
a) Hàm số đã cho đồng biến, nghịch biến trên R.
b) Đồ thị hàm số song song với đường thẳng y = 2x. Vẽ đồ thị với m vừa tìm được.
Câu 4 (2 điểm): Cho đường tròn (O; R), đường kính AB. Vẽ điểm C thuộc đường tròn (O; R) sao cho AC = R. Kẻ OH vuông góc với AC tại H. Qua C vẽ một tiếp tuyến của đường tròn (O; R), tiếp tuyến này cắt đường thẳng OH tại D.
a) Chứng minh AD là tiếp tuyến của đường tròn (O; R).
b) Tính BC theo R và các tỉ số lượng giác của góc ABC.
c) Gọi M là điểm thuộc tia đối của tia CA. Chứng minh: MC.MA = MO2 – AO2
Đáp án đề thi Học kì 1 môn Toán 9 - Đề số 14
Câu 1: Căn bậc hai của 9 là:
A) 81
B) ±81
C) 3
D) ±3
Giải thích: Vì 32 = (-3)2 = 9
Chú ý: = 3 (đây là căn bậc hai số học)
Câu 2: Phương trình 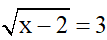 có nghiệm là:
có nghiệm là:
A) 9
B) ±9
C) ±4
D) 11
Giải thích:
Điều kiện: x ≥ 2
Ta có: x – 2 = 32 = 9
x = 9 + 2
x = 11
Câu 3: Điều kiện xác định của 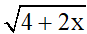 là:
là:
A) x ≥ 0
B) x ≥ 2
C) x ≥ -2
D) x ≤ 2
Giải thích:
Điều kiện xác định: 4 + 2x ≥ 0
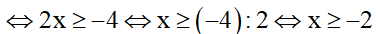
Câu 4: Kết quả của phép khai phương 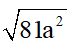 (với a < 0) là:
(với a < 0) là:
A) -9a
B) 9a
C) -9|a|
D) 81a
Giải thích:
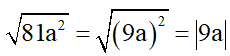
Vì a < 0 nên |9a| = -9a
Câu 5: Tìm x biết 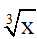 = -5:
= -5:
A) x = -25
B) x = -125
C) x = -512
D) x = 15
Giải thích: 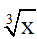 = -5
= -5
<=> x = (-5) = -125
Câu 6: Rút gọn biểu thức 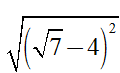 ta được kết quả cuối cùng là:
ta được kết quả cuối cùng là:
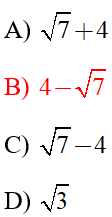
Giải thích : 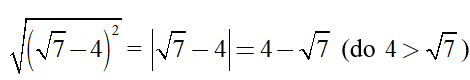
Câu 7: Trong hệ tọa độ Oxy, đường thẳng y = 2 - x song song với đường thẳng:
A) y = -x
B) y = -x + 3
C) y = -1 – x
D) Cả ba đường thẳng trên
Giải thích :
A) y = -x có a = -1; b = 0
B) y = -x + 3 có a = -1; b = 3
C) y = -1 – x có a = -1; b = -1.
Xét đường thẳng ban đầu: y = 2 – x có a = -1 ; b = 2
Cả ba đường thẳng A, B, C đều đúng.
Chọn đáp án D
Câu 8: Trong các hàm số bậc nhất sau, hàm số nào là hàm số nghịch biến:
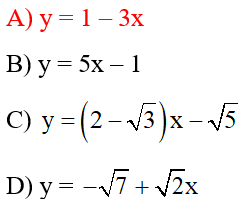
Giải thích: Ở đáp án A, ta có y = 1 – 3x có a = -3 < 0 nên hàm số nghịch biến.
Câu 9: Nếu điểm B(1; -2) thuộc đường thẳng y = x – b thì b bằng:
A) -3
B) -1
C) 3
D) 1
Giải thích: Thay x = 1; y = -2 vào hàm số ta có: -2 = 1 – b
⇔ b = 1 + 2 ⇔ b = 3
Câu10: Cho hai đường thẳng: (d): y = 2x + m – 2 và (d’): y = kx + 4 – m; (d) và (d’) trùng nhau nếu:
A) k = 2 và m = 3
B) k = -1 và m = 3
C) k = -2 và m = 3
D) k = 2 và m = -3
Giải thích: Hai đường thẳng trùng nhau nếu a = a’ và b = b’
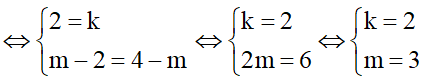
Câu 11: Góc tạo bởi đường thẳng y = x + 1 và trục Ox có số đo là:
A) 450
B) 300
C) 600
D) 1350
Giải thích:
Vì a = 1 > 0 nên tan
Câu 12: Hệ số góc của đường thẳng: y = -4x + 9 là:
A) 4
B) -4x
C) -4
D) 9
Giải thích: Hàm số y = ax + b có hệ số góc là a do đó a = -4
Câu13: Cho tam giác vuông cân ABC đỉnh A có BC = 6cm, khi đó AB bằng
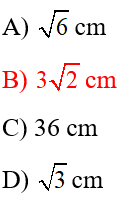
Giải tích:
Tam giác ABC vuông cân tại A nên AB = AC
Áp dụng định lý Py – ta – go cho tam giác vuông ABC ta được:
AB2 + AC2 = BC2
2AB2 = BC2
⇔2AB2 = 62 =36
⇔ AB2 = 36:2 = 18
⇔ AB = 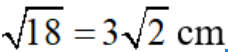
Câu 14: Cho 1 tam giác vuông có hai góc nhọn là và . Biểu thức nào sau đây không đúng:
A) sin α= cosβ
B) cotα= tanβ
C) sin2 α + cos2β = 1
D) tanα = cotβ
Giải thích:
Vì và là hai góc nhọn trong một tam giác vuông nên và là hai góc phụ nhau.
Mà hai góc phụ nhau thì:
sinα = cosβ
cosα = sinβ
cotα = tanβ
tanα = cotβ
Nên đáp án đúng C
Câu 15: Cho tam giác ABC vuông ở A có AC = 3 cm , BC = 5cm. Giá trị của cotB là:
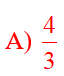
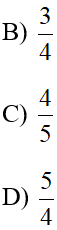
Giải thích:
Xét tam giác vuông ABC vuông tại A: AB² + AC² = BC² (định lý Py – ta – go)
⇔ 32 + AB2 = 52
⇔ AB2 = 52-32 = 25 - 9 = 16
⇔ AB = 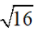 = 4
= 4
CotB = 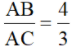
Câu 16: Cho tam giác ABC vuông tại A có AB = 9 cm, AC = 12 cm, BC = 15 cm. Tính độ dài AH là :
A) 8,4 cm
B) 7,2 cm
C) 6,8 cm
D) 4.2 cm
Giải thích:
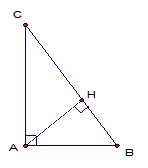
Xét tam giác ABC vuông tại A đường cao AH.
<=> AH.BC = AB.AC
<=> AH.15 = 9.12
<=> AH = 9.12:15
<=> AH = 7,2cm
Câu 17: Tâm của đường tròn ngoại tiếp tam giác là giao điểm của các đường :
A) Trung tuyến
B) Phân giác
C) Đường cao
D) Trung trực
Giải thích:
Tâm của đường tròn ngoại tiếp tam giác là giao của ba đường trung trực ứng với ba cạnh của tam giác.
Câu 18: Hai đường tròn (O) và (O’) tiếp xúc ngoài. Số tiếp tuyến chung của chúng là:
A) 1
B) 2
C) 3
D) 4
Giải thích
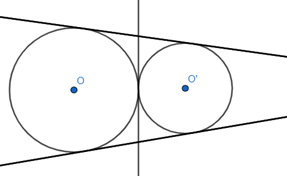
Hai đường tròn tiếp xúc ngoài với nhau sẽ có ba tiếp tuyến chung.
Câu 19: Cho (O; 6cm) và đường thẳng a có khoảng cách đến O là d, điều kiện để đường thẳng a là cát tuyến của đường tròn (O) là:
A) d < 6cm
B) d = 6cm
C) d > 6cm
D) d ≥ 6cm
Giải thích: Vì a là cát tuyến của đường tròn (O) nên a cắt (O) do đó khoảng cách từ O đến a nhỏ hơn R hay d < 6cm
Câu 20: Dây AB của đường tròn (O; 5cm) có độ dài là 6cm. Khoảng cách từ O đến AB bằng:
A) 6cm
B) 7 cm
C) 4 cm
D) 5 cm
Giải thích:
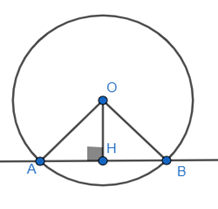
Gọi H là hình chiếu của O lên AB, khi đó OH là khoảng cách từ O đến AB
Tam giác AOB cân tại O nên OH vừa là đường cao vừa là đường trung tuyến.
Do đó H là trung điểm của AB HA = HB = AB:2 = 6:2 = 3cm
Xét tam giác AHO vuông tại H ta có:
AO²= OH² + HA²
⇔ 5² = 3² + OH²
⇔ OH² = 5² - 3² = 16
⇔ OH = 4
II. Tự luận
Câu 1 (1 điểm): Tính:
a) 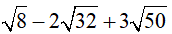
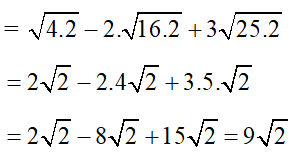
b) 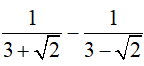
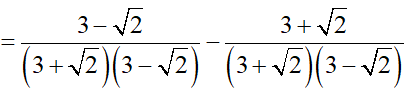
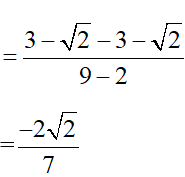
Câu 2 (1 điểm):
a) Điều kiện xác định: x ≥ 0 ; x ≠ 4
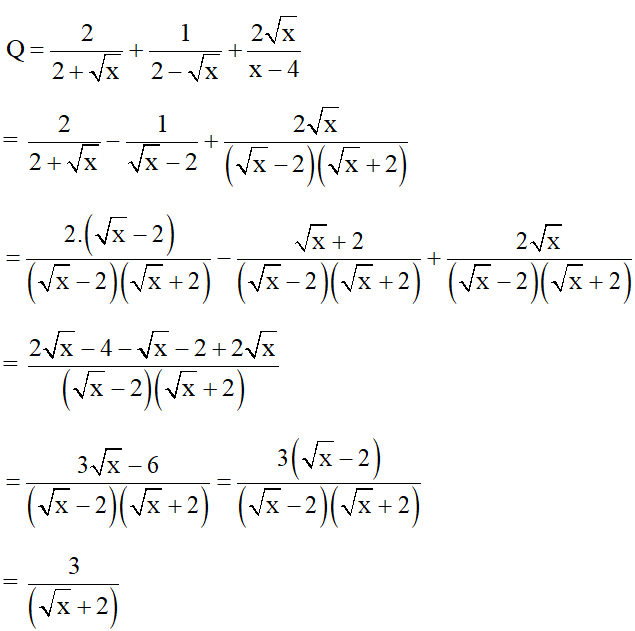
b) Để Q = 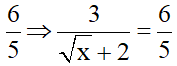
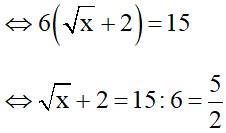
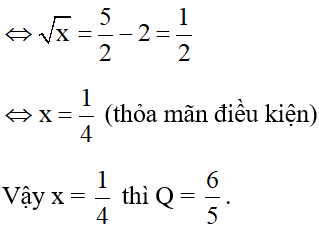
Câu 3 (1 điểm):
a) Hàm số đã cho đồng biến trên R khi m + 1 > 0 m > -1
Hàm số nghịch biến trên R khi m + 1 < 0 m < -1.
b) Đồ thị hàm số song song với đường thẳng y = 2x nên a = 2 hay m + 1 = 2 và -3 0 suy ra m = 1(thỏa mãn)
Vậy hàm số cần tìm là y = 2x – 3
Bảng giá trị:
|
x |
0 |
|
|
y = 2x – 3 |
-3 |
0 |
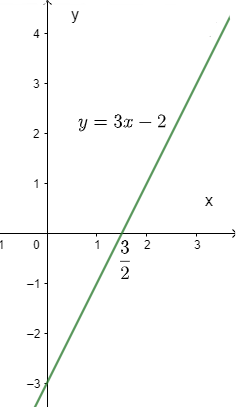
Câu 4 (2 điểm):
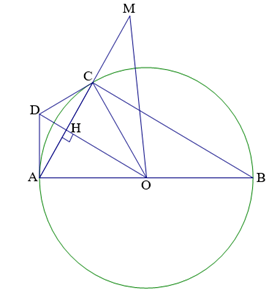
a) Xét tam giác AOC có: AC = OC = OA = R nên tam giác AOC là tam giác đều
Mà OH là đường cao của tam giác AOC (OH vuông góc với AC theo giả thuyết) nên OH là đường phân giác của góc ∠AOC
⇔ ∠AOD = ∠DOC (tính chất)
Xét tam giác AOD và tam giác COD có:
OC = OA = R
∠AOD = ∠DOC
OD là cạnh chung
Do đó ΔAOD = ΔCOD(c – g – c)
⇒ ∠DAO = ∠DCO (hai góc tương ứng)
Lại có CD là tiếp tuyến của (O) nên CD vuông góc với CO ⇒ ∠DCO = 90°
Do đó, ∠DAO= 90° ⇒ DA ⊥ AO tại A
=> AD là tiếp tuyến của (O).
b) Tam giác ACB có CO là đường trung tuyến (vì O là trung điểm của AB)
Lại có CO = AB
Do đó tam giác ABC vuông tại A (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
Áp dụng định lý Py - ta - go vào tam giác vuông ABC có
AB2 = AC2 + BC2
BC2 = AB2 – AC2 = 4R2 – R2 = 3R2
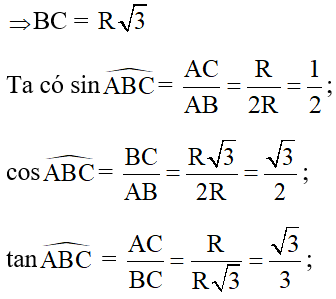
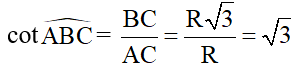
c) Ta có: MC = MH – HC; MA = MH + HA
MC.MA = (MH – HC)(MH + HA)
Lại có OH ⊥ AC tại H HA = HC (quan hệ vuông góc giữa đường kính và dây)
MC.MA = (MH – HA)(MH + HA) = MH2 – HA2
Tam giác AHO vuông tại H, do đó HA2 = AO2 – HO2
MC.MA = MH2 – (AO2 – HO2) = (MH2 + HO2) – AO2
Tam giác MOH vuông tại H, do đó MH2 + HO2 = MO2, thay vào đẳng thức trên ta được: MC.MA = MO2 – AO2
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 1
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Học kì 1 Toán lớp 9 có đáp án - (Đề số 15)
Bài 1 (2 điểm):
Cho A =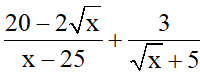 và B =
và B =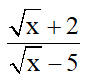 (với x ≥ 0: x ≠ 5).
(với x ≥ 0: x ≠ 5).
a) Tính giá trị của biểu thức B khi x = 49.
b) Rút gọn A
c) Tìm giá trị của x để B:A = |x – 4|.
Bài 2 (2 điểm):
Cho hàm số bậc nhất y = (2m – 1)x – 2m + 5 (với m là tham số) có đồ thị là đường thẳng d và hàm số y = 2x + 1 có đồ thị là đường thẳng (d’).
a) Tìm giá trị của m để đường thẳng (d) đi qua điểm A(2; -3)
b) Tìm giá trị của m để đường thẳng (d) song song với đường thẳng (d’). Với giá trị m vừa tìm được, vẽ đường thẳng (d) và tính góc tạo bởi đường thẳng (d) và trục Ox (làm tròn đến phút).
Bài 3 (2 điểm): Giải phương trình:
a) 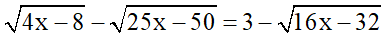
b) 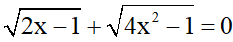
Bài 4 (3 điểm): Cho tam giác ABC nhọn. Đường tròn tâm O, đường kính BC cắt AB ở M cắt AC ở N. Gọi H là giao điểm của BN và CM. AH cắt BC tại K.
a) Chứng minh AK vuông góc với BC
b) Gọi E là trung điểm của AH. Chứng minh EM là tiếp tuyến của đường tròn (O).
c) Cho biết sin 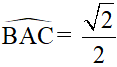 . Hãy so sánh AH và BC.
. Hãy so sánh AH và BC.
Bài 5 (1 điểm):
a) Hải đăng Kê Gà thuộc xã Tân Thành, huyện Hàm Thuận Nam, Bình thuận là ngọn hải đăng được trung tâm sách kỷ lục Việt Nam xác nhận là ngọn hải đăng cao nhất và nhiều tuổi nhất. Hải đăng Kê Gà được xây dựng năm 1897 – 1899 và toàn bộ bằng đá. Tháp đèn có hình bát giác, cao 66m so với mực nước biển. Ngọn đèn đặt trong tháp có thể phát sáng xa tới 40km. Một người trên biển muốn quan sát ngọn hải đăng có độ cao 66m, người đó đứng trên mũi thuyền và dùng giác kế đo được góc giữa thuyền và tia nắng chiều từ đỉnh ngọn hải đăng đến thuyền là . Tính khoảng cách của thuyền đến ngọn hải đăng (làm tròn đến m).

b) Cho các số thực dương x; y thỏa mãn xy > 2020x + 2021y.
Đáp án đề thi Học kì 1 môn Toán 9 - Đề số 15
Bài 1:
a) Thay x = 49 (thỏa mãn điều kiện) vào B ta được:
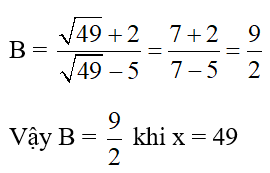
b) A = 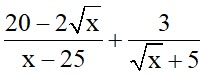
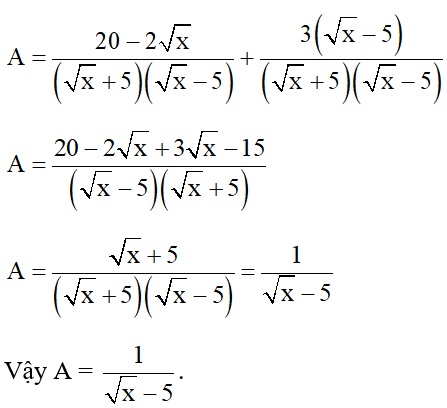
Vậy A = 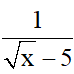 .
.
c) Ta có:
B:A = |x – 4|
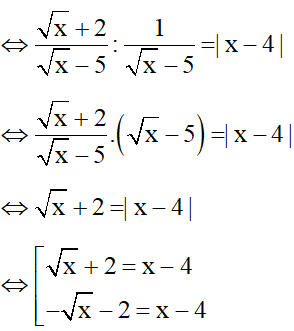
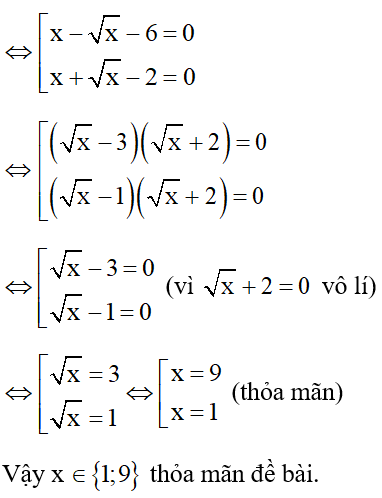
Bài 2:
a) (d) đi qua điểm A(2; -3) khi:
(2m – 1).2 – 2m + 5 = -3
<=> 4m -2 -2m +5 = -3
<=> 2m = -6
<=> m = -3
Vậy m = -3.
b) (d) // (d’) khi và chỉ khi:
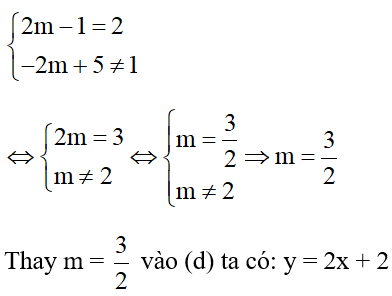
+ Với x = -1 thì y = 0 (d) đi qua điểm A(-1; 0)
+ Với x = 0 thì y = 2 (d) đi qua điểm B(0; 2)
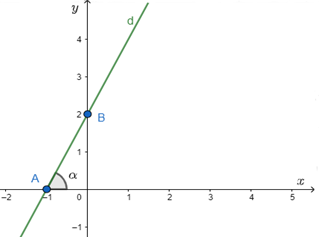
Ta có: 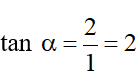
⇒ α = 63°26'
Vậy α = 63°26'
Bài 3:
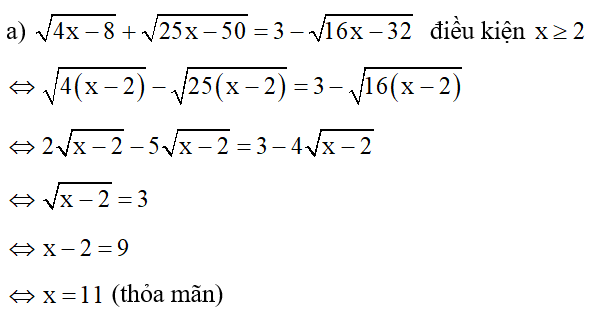
Vậy x = 11
b) 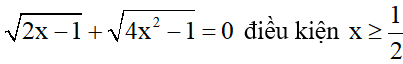
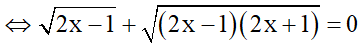
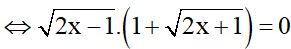
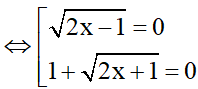
Trường hợp 1: 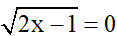
<=> 2x -1 = 0
<=> 2x = 1
<=> x = ½ (thỏa mãn)
Trường hợp 2: 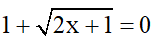
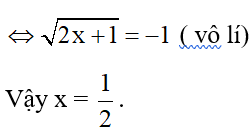
Bài 4:
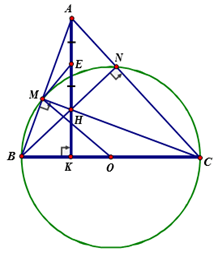
a) Xét tam giác BMC có:
OM = OB = OC = 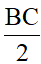 = R
= R
Tam giác BMC vuông tại M (tính chất đường trung tuyến ứng với cạnh huyền)
⇒ BM ⊥ MC(1)
Chứng minh tương tự ta có BN ⊥ NC (2)
Từ (1) và (2) suy ra BN, CM là hai đường cao của tam giác ABC
Suy ra H là trực tâm của tam giác ABC (do H là giao của hai đường cao BN và CM)
⇒ AH ⊥ BC hay AK ⊥ BC .
b) Xét tam giác AMH vuông tại M, ME là đường trung tuyến (do E là trung điểm của AH theo gt)
⇒ AE = EM ⇒ ΔAEM cân
⇒ ∠EAM = ∠EMA (tính chất tam giác cân) (3)
Ta có: ∠EAM = ∠MCB (cùng phụ với góc ∠ABC) (4)
Lại có tam giác BMC vuông tại M, MO là đường trung tuyến nên MO = OC do đó tam giác MOC cân tại O
⇒ ∠OCM = ∠OMC (tính chất) (5)
Từ (3); (4); (5) ta có:
∠AME = ∠OMC
Lại có:
∠AME + ∠EMH = 90°
⇒∠OMC + ∠EMH = 90° hay ∠OME = 90°
⇒ MO ⊥ ME
Lại có ME có điểm chung với đường tròn (O) là M nên ME là tiếp tuyến của đường tròn (O).
c) Vì sin 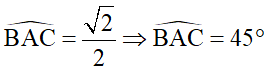
⇒ ΔAMC vuông cân tại M ⇒ AM = MC
Xét tam giác AMH và tam giác CMB có:
∠MAH = ∠MCB (cùng phụ với góc B)
AM = CM
∠MAH = ∠MCB = 90°
=> ΔAMH = ΔCMB (g – c – g)
=> AH = BC
Bài 5:
a) Giả sử khoảng cách từ thuyến đến ngọn hải đăng, chiều cao ngọn hải đăng và tia nắng chiếu từ đỉnh ngọn hải đăng đến thuyến tạo thành một tam giác vuông ABC, với AB là chiều cao ngọn hải đăng, AC là khoảng cách từ ngọn hải đăng đến thuyền.
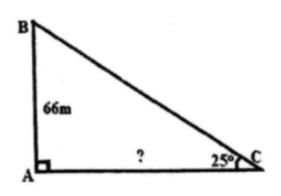
Xét tam giác ABC vuông tại A, ta có:
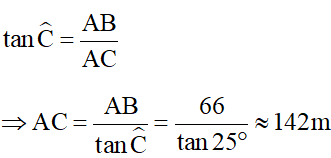
Vậy khoảng cách của thuyền đến ngọn hải đăng là 142m.
b) Biến đổi giả thiết bài toán thành:
xy > 2020x + 2021y
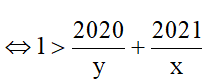
Do đó, ta có:
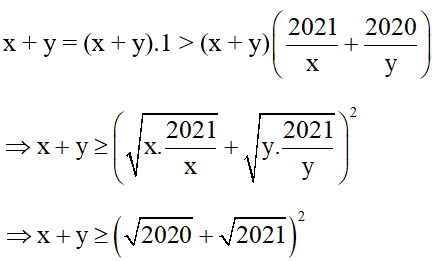
Theo bất đẳng thức Bunhiacopski ta có điều phải chứng minh.