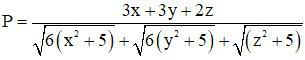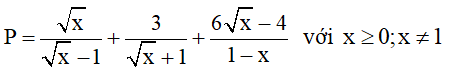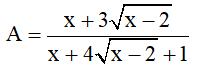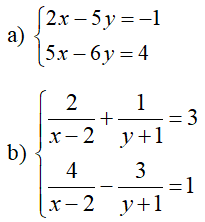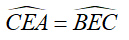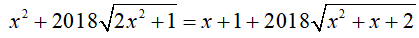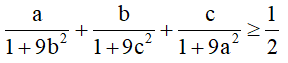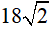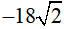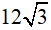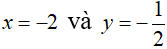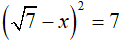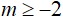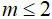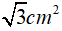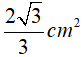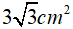Bộ 30 đề thi Giữa học kì 2 Toán lớp 9 có đáp án
Bộ 30 đề thi Giữa học kì 2 Toán lớp 9 có đáp án giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 9 Giữa học kì 2. Mời các bạn cùng đón xem:
[Năm 2023] Đề thi Giữa học kì 2 Toán lớp 9 có đáp án
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 1)
Câu 1 (2 điểm).
1) Thực hiện phép tính: 
2) Với giá trị nào của m thì hàm số y = (1 - 2m)x - 5 đồng biến trên R.
3) Giải hệ phương trình: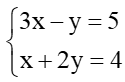 
Câu 2 (3 điểm ).
1) Cho phương trình: x2 + 2(m-1) x + m2 + m - 2 = 0.
a) Giải phương trình với m = -2.
b) Tìm m để phương trình có nghiệm .
2) Cho biểu thức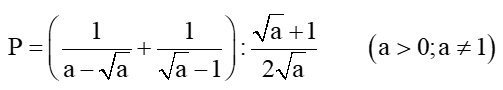 
a) Rút gọn biểu thức P
b) Tìm a để P < -1.
Câu 3 (1,5 điểm).
Hai ô tô khởi hành cùng một lúc từ hai tỉnh A và B cách nhau 150 km đi ngược chiều nhau và gặp nhau sau 1 giờ 30 phút. Tính vận tốc của mỗi ô tô, biết vận tốc của ô tô đi từ A lớn hơn vận tốc của ô tô đi từ B là 20 km/h.
Câu 4 (3 điểm).
Cho tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD tại F. Chứng minh rằng:
a) Tứ giác DCFE nội tiếp được
b) góc CDE = góc CFE
c) Tia CA là tia phân giác của góc BCF
Câu 5 (0,5 điểm).
Cho a, b, c là ba số dương.
Chứng minh rằng: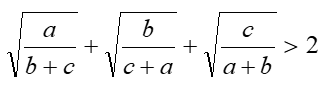 
_______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 2)
I. TRẮC NGHIỆM KHÁCH QUAN: (2 điểm)
Khoanh tròn vào các chữ cái đứng trước các câu trả lời đúng trong mỗi câu sau:
Câu 1: Cho phương trình 2x – y = 5. Phương trình nào sau đây kết hợp với phương trình đã cho để được một hệ phương trình có vô số nghiệm?
|
A. x – y = 5 |
B. – 6x + 3y = 15 |
C. 6x + 15 = 3y |
D. 6x – 15 = 3y. |
Câu 2: Trong các hàm số sau, hàm số nào đồng biến khi x < 0?
Câu 3: Cho hàm số y = f(x) = 2ax2 (Với a là tham số). Kết luận nào sau đây là đúng?
A. Hàm số f(x) đạt giá tri lớn nhất bằng 0 khi a < 0.
B. Hàm số f(x) nghịch biến với mọi x < 0 khi a > 0
C. Nếu f(-1) = 1 thì a = 1/2
D. Hàm số f(x) đồng biến khi a >0
Câu 4: Trong mặt phẳng tọa độ Oxy, đồ thị các hàm số y = 2x2 và y = 3x – 1 cắt nhau tại hai điểm có hoành độ là:
Câu 8: Mệnh đề nào sau đây là sai:
A. Hình thang cân nội tiếp được một đường tròn.
B. Hai cung có số đo bằng nhau thì bằng nhau.
C. Hai cung bằng nhau thì có số đo bằng nhau.
D. Hai góc nội tiếp bằng nhau thì cùng chắn một cung.
II. PHẦN TỰ LUẬN( 8 điểm):
Bài 1:(2điểm)
Cho phương trình x2 – mx + m – 1 = 0 (1)
a) Giải phương trình (1) với m = -2
b) Chứng tỏ phương trình (1) luôn có nghiệm x1, x2 với mọi giá trị của m.
c) Tìm giá trị của m để phương trình (1) có 1 nghiệm bằng 3 . Tìm nghiệm còn lại
Bài 2: (2 điểm)
a, Vẽ đồ thị hàm số 
(P)
b, Tìm giá trị của m sao cho điểm C(-2; m) thuộc đồ thị (P)
c, Tìm tọa độ giao điểm của đường thẳng y = x - 0,5 và parabol (P)
Bài 3: (3 điểm)
Cho nửa đường tròn (O) đường kính AB. Kẻ tiếp tuyến Bx với nửa đường tròn.
Gọi C là điểm trên nửa đường tròn sao cho cung CB bằng cung CA, D là một điểm tuỳ ý trên cung CB ( D khác C và B ). Các tia AC, AD cắt tia Bx theo thứ tự là E và F .
a, Chứng minh tam giác ABE vuông cân.
b, Chứng minh 
c, Chứng minh tứ giác CDFE nội tiếp được
Bài 4: (1điểm) Giải hệ phương trình: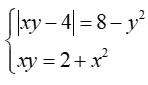 
_______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 3)
Bài 1 (2,0 điểm) : Cho biểu thức 
a) Rút gọn P
b) Tìm giá trị của x để P = -1
c) So sánh P với 1
Bài 2 (2,0 điểm) : Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Một xe khách và một xe du lịch khởi hành đồng thời từ A đến B. Biết vận tốc của xe du lịch lớn hơn vận tốc của xe khách là 20km/h. Do đó nó đến B trước xe khách 50 phút. Tính vận tốc của mỗi xe, biết quãng đường AB dài 100km.
Bài 3 (2,0 điểm) : Cho hàm số y = ax2 với a ≠ 0 có đồ thị là parabol (P)
a) Xác định a biết parabol (P) đi qua điểm A(-1;1)
b) Vẽ đồ thị của hàm số y = ax2 với a vừa tìm được ở trên
c) Cho đường thẳng (d): y = 2x + 3 Tìm tọa độ giao điểm của (d) và (P) với hệ số a tìm được ở câu a.
d) Tính diện tích tam giác AOB với A và B là giao điểm của (P) và (d)
Bài 4 (3,5 điểm) : Cho đường thẳng d và đường tròn (O; R) không có điểm chung. Kẻ OH vuông góc với đường thẳng d tại H. Lấy điểm M bất kì thuộc d. Qua M kẻ hai tiếp tuyến MA, MB tới đường tròn (O; R). Nối AB cắt OH, OM lần lượt tại K và I.
a) Chứng minh 5 điểm M, H, A, O, B cùng thuộc một đường tròn
b) Chứng minh OK.OH = OI.OM
c) Chứng minh khi M di chuyển trên d thì đường thẳng AB đi qua một điểm cố định
d) Tìm vị trí của M để diện tích tam giác OIK đạt giá trị lớn nhất.
Bài 5 (0,5 điểm) : Tìm giá trị nhỏ nhất của biểu thức 
______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 4)
Bài 1 : Giải các hệ phương trình:
Bài 2 : Giải toán bằng cách lập phương trình hoặc hệ phương trình:
Theo kế hoạch hai tổ được giao sản xuât sản phẩm trong một thời gian đã định. Do cải tiến kỹ thuật nên tổ đã sản xuất vượt mức kế hoạch và tổ sản xuất vượt mức kế hoạch . Vì vậy trong cùng một thời gian quy định hai tổ đã hoàn thành vượt mức sản phẩm. Tính số sản phẩm được giao của mỗi tổ theo kế hoạch.
Bài 3 :
a) Vẽ parabol (P): y = 2x2 .
b) Viết phương trình đường thẳng (d) cắt parabol (P) tại hai điểm A và B có hoành độ lần lượt là -1 và 2 .
Bài 4 : Cho đường tròn (O;R) . Từ điểm A nằm ngoài đường tròn kẻ hai tiếp tuyến AB, AC với đường tròn ( B,C là hai tiếp điểm). Từ B kẻ đường thẳng song song với AC cắt O tại D (D khác B ), đường thẳng AD cắt O tại E ( E khác D ).
a) Chứng minh tứ giác ΔAOC nội tiếp.
b) Chứng minh: AE.AD = AB2
c) Chứng minh 
d) Giả sử OA = 3R . Tính khoảng cách giữa hai đường thẳng AC và BD theo R .
Bài 5 : Giải phương trình:
_______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 5)
Bài 1 (2,5 điểm) : Trong mặt phẳng tọa độ Oxy, cho Parabol (P): y = x2 và đường thẳng (d): y = -x + 2
a) Tìm tọa độ giao điểm của (P) và (Q)
b) Gọi A, B là hai giao điểm của (P) và (Q). Tính diện tích tam giác OAB.
Bài 2 (2,5 điểm) : Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Trong tháng đầu, hai tổ sản xuất được 860 chi tiết máy. Đến tháng thứ hai, tổ I vượt mức 15%, tổ II vượt mức 10%. Do đó, tháng thứ hai cả 2 tổ sản xuất được 964 chi tiết máy. Tính số chi tiết máy mỗi tổ đã sản xuất được trong tháng đầu.
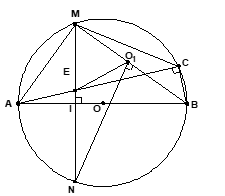
Bài 3 (4,0 điểm) : Cho đường tròn tâm O đường kính AB. Dây CD vuông góc với AB tại E (E nằm giữa A và O; E không trùng A, không trùng O). Lấy điểm M thuộc cung nhỏ BC sao cho cung MB nhỏ hơn cung MC. Dây AM cắt CD tại F. Tia BM cắt đường thẳng CD tại K.
a) Chứng minh tứ giác BMFE nội tiếp
b) Chứng minh BF vuông góc với AK và
c) Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.
Bài 4 (1,0 điểm) : Với các số a, b, c > 0 và thỏa mãn a + b + c = 1
Chứng minh 
_______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 6)
Bài 1 (2 điểm) Giải các hệ phương trình sau:
a.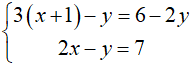 
b. 
B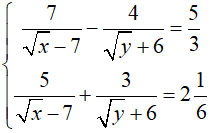ài 2 (2 điểm) Gải bài toán bằng cách lập phương trình hoặc hệ phương trình’
Hai tổ sản xuất trong tháng thứ nhất làm được 1000 sản phẩm. Sang tháng thứ hai, do cải tiến kĩ thuật nên tổ một vượt mức 20%, tổ hai vượt mức 15% so với tháng thứ nhất. Vì vậy, cả hai tổ sản xuất được 1170 sản phẩm. Hỏi tháng thứ nhất, mỗi tổ sản xuất được bao nhiêu sản phẩm?
Bài 3 (2 điểm)
Cho đường thẳng (d) có phương trình y = ax + b. Tìm a, b biết (d) song song với đường thẳng (d’) có phương trình: y = -3x + 5 và đi qua điểm A thuộc Parabol (P) có phương trình y = x2 có hoành độ bằng – 2.
Bài 4 (3,5 điểm) Cho đường tròn (O; R), kẻ đường kính AB. Điểm M bất kì trên (O) sao cho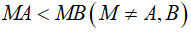 
. Từ M kẻ 
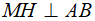tại H. Vẽ đường tròn (I) đường kính MH cắt MA, MB lần lượt tại E và F.
a. Chứng minh: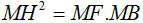 
và ba điểm E, I, F thẳng hàng.
b. Kẻ đường kính MD của đường tròn (O), MD cắt đường tròn (I) tại điểm thứ hai là N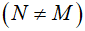 
. Chứng minh tứ giác BONF nội tiếp.
c. MD cắt EF tại K. Chứng minh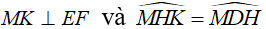 
d. Đường tròn (I) cắt đường tròn (O) tại điểm thứ hai là P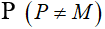 
. Chứng minh ba đường thẳng MP, FE và BA đồng quy.
Bài 5 (0,5 điểm) Cho các số không âm x, y, z thỏa mãn x + y + z = 1. Tìm giá trị lớn nhất của biểu thức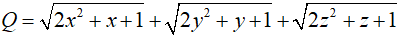 
Đáp án đề thi Giữa kì 2 môn Toán 9 - Đề số 6
Câu 1:
a. Ta có:
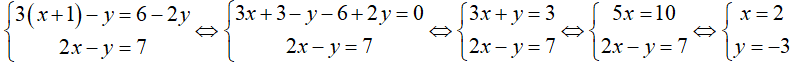
vậy nghiệm của hệ phương trình là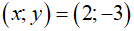 
b. Điều kiện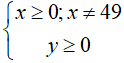 
Ta có:
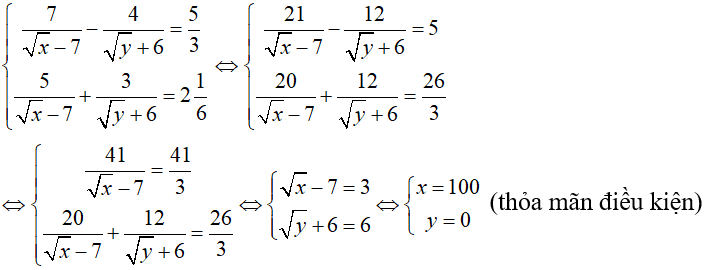
Vậy nghiệm của hệ phương trình là: (x; y) = (100;0)
Câu 2:
Gọi số sản phẩm tổ 1 và tổ 2 làm được trong tháng thứ nhất lần lượt là x, y (sản phẩm) điều kiện: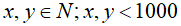 
Lập luận đưa về hệ phương trình: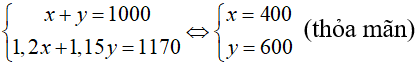 
Câu 3:
Điểm A thuộc y = x2 có hoành độ x = -2 ⇒ y = (-2)2 = 4 ⇒ A(-2;4)
Vì đường thẳng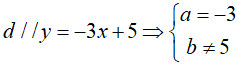 
Vì đường thẳng (d) qua A (-2; 4) nên: -3.(-2) + b = 4 ⇒ b = -2(tm) ⇒ (d) : y = -3x - 2
Câu 4:
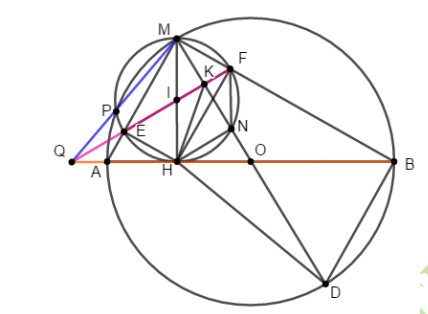
a. Chứng minh: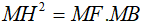 
và ba điểm E, I, F thẳng hàng.
Ta có: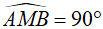 
(góc nội tiếp chắn nửa đường tròn tâm O) và 
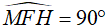(góc nội tiếp chắn nửa đường tròn tâm I)
Suy ra tam giác MHB vuông tại H, đường cao HF
Vậy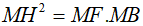 
(hệ thức lượng trong tam giác vuông)
b. Kẻ đường kính MD của đường tròn (O), MD cắt đường tròn (I) tại điểm thứ hai là N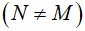 
. Chứng minh tứ giác BONF nội tiếp.
Ta có: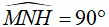 
(góc nội tiếp chắn nửa đường tròn tâm I)
Suy ra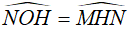 
(cùng phụ góc 
)
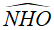Mà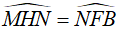 
(do tứ giác MHNF nội tiếp)
Nên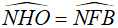 
Mặt khác ta có: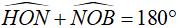 
(kề bù) nên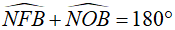 
Vậy tứ giác BONF nội tiếp (tứ giác có tổng hai góc đối bằng 180°)
c. MD cắt EF tại K. Chứng minh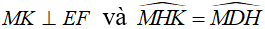 
Ta có: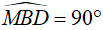 
(góc nội tiếp chắn nửa đường tròn)
Chứng minh tương tự câu a, ta được tam giác AMH vuông tại H, đường cao HE.
Khi đó: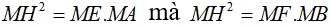 
(câu a) nên tam giác MAB đồng dạng tam giác MFE
Suy ra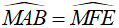 
(hai góc tương ứng bằng nhau)
Mặt khác ta có: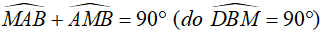 
Ta có tam giác MKF đồng dạng với tam giác MBD (g.g)
Suy ra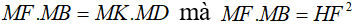 
(câu a)
Nên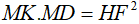 
Khi đó tam giác MHK đồng dạng với tam giác MDH (c.g.c)
Vậy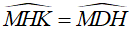 
(hai góc tương ứng)
d. Đường tròn (I) cắt đường tròn (O) tại điểm thứ hai là P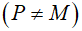 
. Chứng minh ba đường thẳng MP, FE và BA đồng quy.
Gọi Q là giao điểm của PM và AB.
Xét tam giác MQO có:
MH là đường cao
OI là đường cao (vì OI là đường nối tâm của hai đường tròn)
MH cắt OI tại I
Suy ra I là trực tâm tam giác MQO
Nên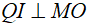 
Mặt khác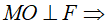 
2 điểm Q, E, F thẳng hàng
Vậy ba đường thẳng MP, EF và BA đồng quy.
Câu 5:
Các em chứng minh bất đẳng thức: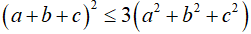 
(chứng minh bằng cách khai triển rồi đưa về dạng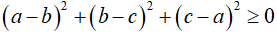 
)
Áp dụng:
_______________________________________________________________________
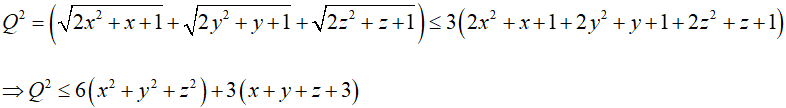
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 7)
Bài 1 (2,0 điểm)
Cho hai biểu thức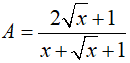 
và 
với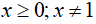 
a. Tính giá trị của biểu thức A khi x = 16
b. Rút gọn biểu thức P
c. Tìm giá trị lớn nhất của biểu thức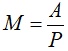 
Bài 2 (2,0 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Hai xí nghiệp cùng may một loại áo. Nếu xí nghiệp thứ nhất may trong 5 ngày và xí nghiệp thứ hai may trong 3 ngày thì cả hai xí nghiệp may được 2620 chiếc áo. Biết rằng trong một ngày xí nghiệp thứ hai may được nhiều hơn xí nghiệp thứ nhất 20 chiếc áo. Hỏi mỗi xí nghiệp một ngày may được bao nhiêu chiếc áo?
Bài 3 (2,0 điểm)
1. Giải hệ phương trình sau: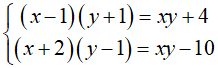 
2. Cho hàm số y = x2 có đồ thị là Parabol (P) và hàm số y = x + 2 có đồ thị là đường thẳng (d)
a. Hãy xác định tọa độ các giao điểm A, B của hai đồ thị hàm số trên
b. Tính diện tích của tam giác OAB (O là gốc tọa độ)
Bài 4 (3,5 điểm)
Cho tam giác ABC nhọn nội tiếp đường tròn (O; R) với cạnh AB cố định khác đường kính. Các đường cao AE, BF của tam giác ABC cắt nhau tại H và cắt đường tròn lần lượt tại I, K, CH cắt AB tại D
a.Chứng minh tứ giác CEHF nội tiếp được trong một đường tròn.
b.Chứng minh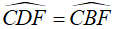 
c.Chứng minh EF // IK
d.Chứng minh rằng khi C chuyển động trên cung lớn AB thì đường tròn ngoại tiếp tam giác DEF luôn đi qua một điểm cố định
Bài 5 (0,5 điểm)
Giải phương trình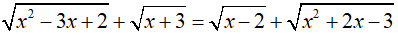 
Đáp án đề thi Giữa học kì 2 môn Toán 9 - Đề số 7
Câu 1:
a. Với x = 16 (thỏa mãn điều kiện) thay vào biểu thức A ta được:
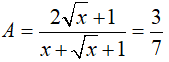
b. Với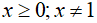 
ta có:
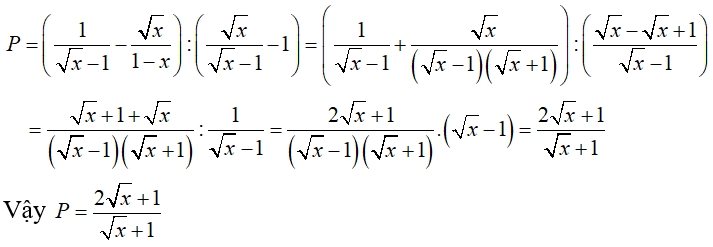
c. Ta có:
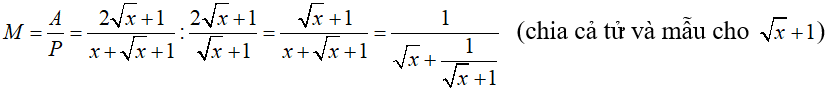
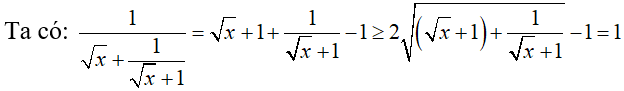
Nên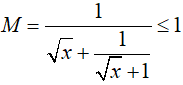 
. Dấu bằng xảy ra khi 
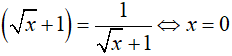(thỏa mãn)
Vậy GTLN M = 1 khi x = 0
Câu 2:
Gọi số áo mà xí nghiệp 1 và xí nghiệp 2 may trong 1 ngày lần lượt là x, y (chiếc áo), điều kiện: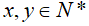 
Lập luận được hệ phương trình: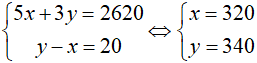 
(thỏa mãn)
Câu 3:
1.
Ta có:
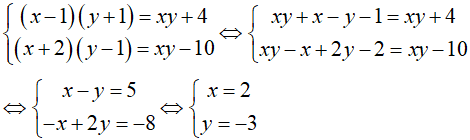
2.
a. Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình: x2 = x + 2. Giải phương trình trên tìm được: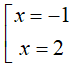 
Với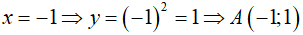 
Với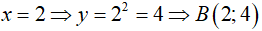 
b. Gọi giao điểm của đường thẳng (d) với Oy là C ⇒ C(0;2)
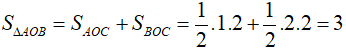(đơn vị diện tích)
Câu 4:
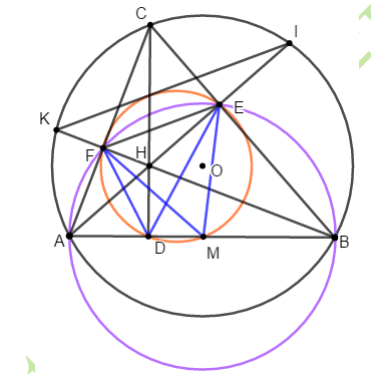
1. Chứng minh tứ giác CEHF nội tiếp được trong một đường tròn
Ta có hai đường cao AE và BE của tam giác ABC cắt nhau tại H nên H là trực tâm tam giác ABC. Khi đó CD vuông góc với AB.
Xét tứ giác CEHF có:
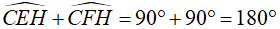
⇒ tứ giác CEHF nội tiếp trong một đường tròn (tứ giác có tổng hai góc đối bằng 180° )
2. Chứng minh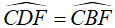 
Xét tứ giác CFDB có:
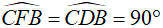
⇒ tứ giác CFDB nội tiếp đường tròn (tứ giác có hai góc cùng nhìn một cạnh bằng nhau)
Vậy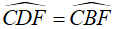 
(góc nội tiếp chắn cung CF)
3. Chứng minh EF // IK
Chứng minh tương tự ý 2, ta được tứ giác AFEB nội tiếp đường tròn
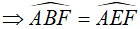(cùng chắn cung AF)
Mà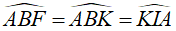 
(cùng chắn cung AK)
Nên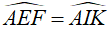 
Vậy EF // IK (hai góc ở vị trí đồng vị bằng nhau)
4. Chứng minh rằng khi C chuyển động trên cung lớn AB thì đường tròn ngoại tiếp tam giác DEF luôn đi qua một điểm cố định
Gọi M là trung điểm BC
Xét đường tròn ngoại tiếp tứ giác AFEB, có AB là đường kính (vì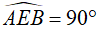 
)
Suy ra M là tâm của đường tròn ngoại tiếp tứ giác AFFEB
Khi đó,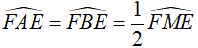 
(góc nội tiếp chắn cung nhỏ bằng nửa số đo góc ở tâm)
Mặt khác, ta chứng minh được các tứ giác AFHD và BEHD nội tiếp
Khi đó,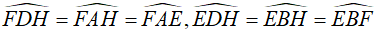 
(Các góc nội tiếp cùng chắn một cung)
Xét tứ giác EFDM, có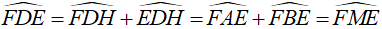 
Suy ra tứ giác EFDM nội tiếp đường tròn. Vậy đường tròn ngoại tiếp tam giác DEF luôn đi qua điểm M cố định khi điểm C di chuyển trên cung lớn AB.
Câu 5:
Điều kiện rồi đặt nhân tử chung
_______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phú
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án -( Đề số 8)
Bài 1 (2,5 điểm)
Trong mặt phẳng tọa độ Oxy, cho Parabol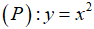 
và đường thẳng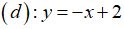 
a .Tìm tọa độ giao điểm của (P) và (Q).
b.Gọi A, B là hai giao điểm của (P) và (Q). Tính diện tích tam giác OAB,
Bài 2 (2,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Trong tháng đầu, hai tổ sản xuất được 860 chi tiết máy. Đến tháng thứ hai, tổ I vượt mức 15%, tổ II vượt mức 10%. Do đó, tháng thứ hai cả 2 tổ sản xuất được 964 chi tiết máy. Tính số chi tiết máy mỗi tổ đã sản xuất được trong tháng đầu.
Bài 3 (4,0 điểm)
Cho đường tròn tâm O đường kính AB. Dây CD vuông góc với AB tại E (E nằm giữa A và O; E không trùng A, không trùng O). Lấy điểm M thuộc cung nhỏ BC sao cho cung MB nhỏ hơn cung MC. Dây AM cắt CD tại F. Tia BM cắt đường thẳng CD tại K.
a.Chứng minh tứ giác BMFE nội tiếp.
b.Chứng minh BF vuông góc với AK và EK.EF = EA.EB
c.Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.
Bài 4. (1,0 điểm) Với các số a, b, c > 0 và thỏa mãn a + b + c = 1
Chứng minh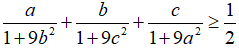 
Đáp án đề thi Giữa học kì 2 môn Toán 9 - Đề số 8
Câu 1:
a. Hoành độ giao điểm của (P) và (Q) là nghiệm của phương trình:
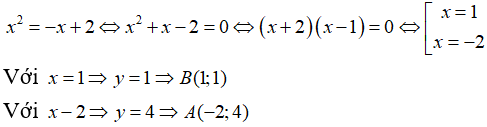
b. Gọi A, B là hai giao điểm của (P) và )Q). Tính diện tích tam giác OAB.
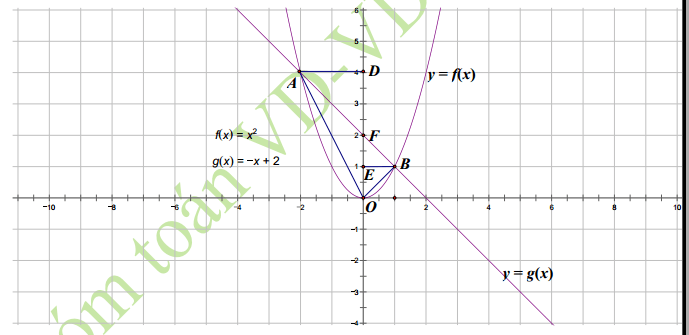
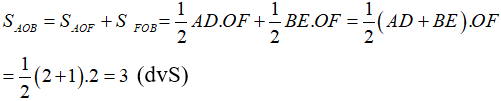
Câu 2:
Gọi số chi tiết máy mỗi tổ đã sản xuất được trong tháng đầu là x, y (
, chi tiết máy)
Vì trong tháng đầu, hai tổ sản xuất được 860 chi tiết máy nên ta có phương trình:
Vì đến tháng thứ hai, tổ I vượt mức 15%, tổ II vượt mức 10%. Do đó, tháng thứ hai cả 2 tổ sản xuất được 964 chi tiết máy, nên ta có phương trình:
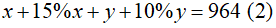
Từ (1) và (2) ta có hệ phương trình:
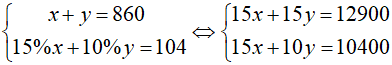
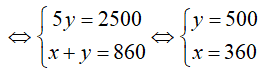
Vậy trong tháng đầu, số chi tiết máy mỗi tổ đã sản xuất được lần lượt là: 360 và 500.
Câu 3:
a. Chứng minh tứ giác BMFE nội tiếp.
Ta có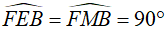 
Nên 4 điểm E, F, M, B cùng thuộc đường tròn đường kính BF, suy ra tứ giác BMFE nội tiếp.
b. Chứng minh BF vuông góc với AK và EK.EF = EA.EB
Nên F là trực tâm, suy ra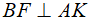 
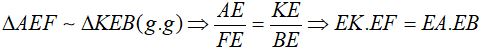
c. Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.
Ta có:
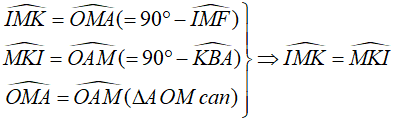
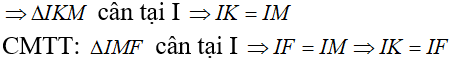
Câu 4:
Ta có:
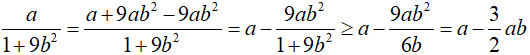
CMTT:
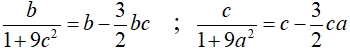
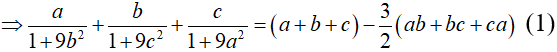
Mặt khác:
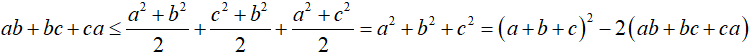
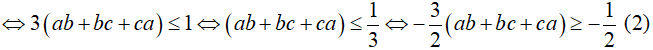
Từ (1) và (2)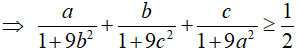 
Dấu “=” xảy ra khi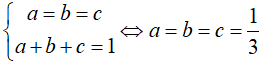 
_______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 9)
I.PHẦN TRẮC NGHIỆM (2,0 điểm)
(Hãy chọn phương án đúng và viết chữ cái đứng trước phương án đó vào bài làm)
Câu 1. Rút gọn biểu thức 
được kết quả là:
Câu 2. Phương trình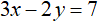 
có nghiệm là:
Câu 3. Đồ thị hàm số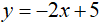 
đi qua điểm có tọa độ là
Câu 4. Phương trình nào sau đây có ít nhất một nghiệm nguyên?
Câu 5. Phương trình (m là tham số) có nghiệm khi và chỉ khi:
Câu 6. Cho đường tròn tâm (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau tại A. Khi đó bằng:
Câu 7. Cho tam giác đều MNE ngoại tiếp đường tròn bán kính 1 cm. Diện tích của tam giác MNE bằng:
Câu 8. Cho hình vuông ABCD, M là trung điểm của BC. Khi đó ta có bằng:
II.PHẦN TỰ LUẬN (8,0 điểm)
Câu 1 (1,5 điểm)
a. Rút gọn biểu thức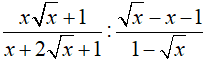 
b. Cho hàm số y = -3x - m + 1, với m là tham số. Xác định giá trị của m để đồ thị hàm số y = -3x - m + 1 đi qua gốc tọa độ O
Câu 2 (1,75 điểm)
a. Giải phương trình x2 - x - 6 = 0
b. Cho phương trình mx2 - 2(m-1)x + m = 0 (1), với m là tham số. Xác định giá trị của m để phương trình (1) có hai nghiệm phân biệt.
Câu 3 (0,75 điểm) Giải hệ phương trình 
Câu 4 (3,25 điểm) Cho đường tròn (O) đường kính BC. Trên đường tròn (O) lấy điểm A sao cho AB < AC. Trên OC lấy điểm M sao cho M nằm giữa O và C. Qua M kẻ đường thẳng vuông góc với OC cắt tia đối của tia AB tại N, cắt AC tại F. Đường thẳng NM cắt đường tròn (O) tại F và K (F nằm giữa E và N)
a. Chứng minh bốn điểm A, B, M, E cùng thuộc một đường tròn và chứng minh bốn điểm N, A, M, C cùng thuộc một đường tròn.
b. Vẽ tiếp tuyến tại A của đường tròn (O) cắt MN tại H. Chứng minh tam giác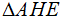 
là tam giác cân.
c. Gọi giao điểm thứ hai của NC với đường tròn (O) là D. Chứng minh HD là
tiếp tuyến của đường tròn (O).
Câu 5 (0,75) Giải phương trình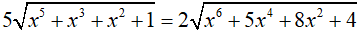 
Đáp án đê thi Giữa học kì 2 môn Toán 9 - Đề số 9
I.PHẦN TRẮC NGHIỆM (2,0 điểm)
Câu 1:
Chọn B
Ta có: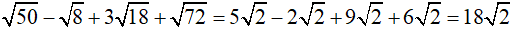 
Câu 2:
Chọn B
Ta có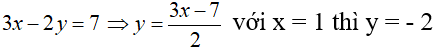 
Câu 3:
Chọn B
Thế x = - 3 vào hàm số ta được y = 11
Suy ra đồ thị hàm số y = -2x + 5 đi qua điểm (-3; 11)
Câu 4:
Chọn C
Xét phương án C: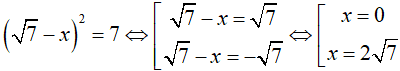 
Phương trình có một nghiệm nguyên x = 0.
Câu 5:
Chọn D
Phương trình đã cho có nghiệm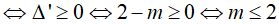 
Câu 6:
Chọn A
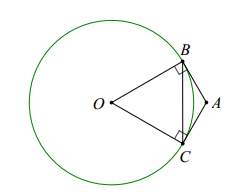
Ta có: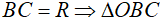 
là tam giác đều
Câu 7:
Chọn C
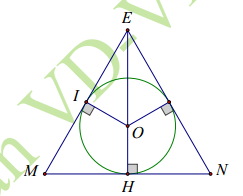
Gọi O là tâm đường tròn nội tiếp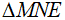 
, I là tiếp điểm của (O) và EM
Xét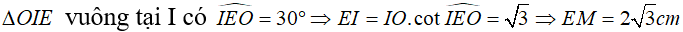 
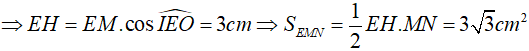
Câu 8:
Chọn D
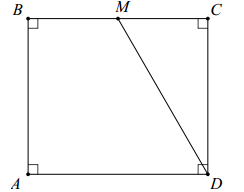
Ta có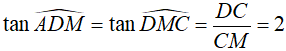 
II.PHẦN TỰ LUẬN (8,0 điểm)
Câu 1:
a. Ta có: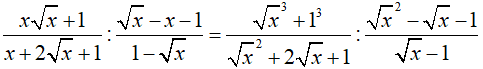 
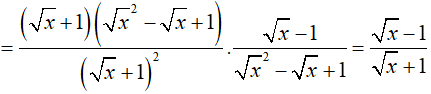
b. Đồ thị hàm số đi qua gốc tọa độ O
Câu 2:
a. Ta có: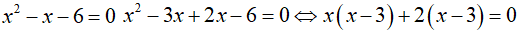 
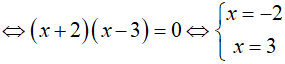
Vậy tập nghiệm của phương trình là: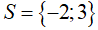 
b. Phương trình đã cho có hai nghiệm phân biệt
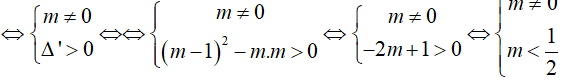
Vậy phương trình (1) có hai nghiệm phân biệt khi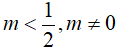 
Câu 3:
Điều kiện: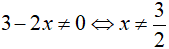 
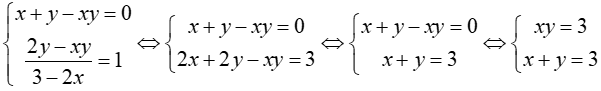
x, y là nghiệm của phương trình:
X2 - 3X + 3 = 0 phương trình vô nghiệm nên hệ đã cho vô nghiệm.
Câu 4:
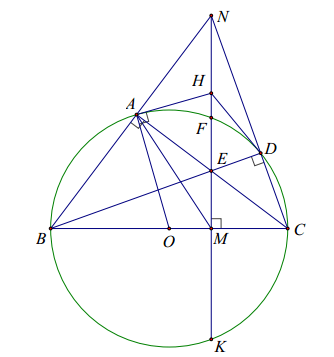
a. Chứng minh bốn điểm A, B, M, E cùng thuộc một đường tròn và chứng minh bốn điểm N, A, M, C cùng thuộc một đường tròn.
Xét tứ giác ABME ta có:
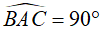(góc nội tiếp chắn nửa đường tròn)
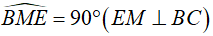
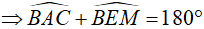
Suy ra tứ giác ABME nội tiếp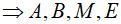 
cùng thuộc một đường tròn.
Xét tứ giác AMCN ta có:
A nhìn NC với 1 góc vuông
M nhìn NC với 1 góc vuông
A, M là hai đỉnh liền kề
Suy ra tứ giác AMCN nội tiếp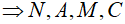 
cùng thuộc một đường tròn
b. Vẽ tiếp tuyến tạ A của đường tròn (O) cắt MN tại H. Chứng minh tam giác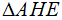 
là tam giác cân.
Ta có tứ giác ABME nội tiếp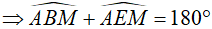 
mà 
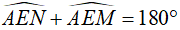
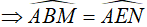(1)
Xét đường tròn (O) ta có:
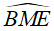là góc tạo bởi tia tiếp tuyến và dây cung chắn cung AC.
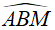là góc nội tiếp chắn cung AC
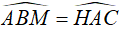(2)
Từ (1) và (2) suy ra 
là tam giác cân tại H
c. Gọi giao điểm thứ hai của NC với đường tròn (O) là D. Chứng minh HD là
tiếp tuyến của đường tròn (O).
ta có: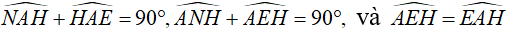 
là tam giác cân tại H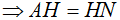 
mà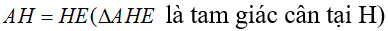 
suy ra H là trung điểm của NE
Xét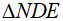 
vuông tại D có DH là trung tuyến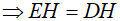 
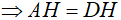
Xét 2 tam giác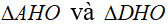 
ta có:
OH là cạnh chung
AH = DH (cmt)
OA = OD
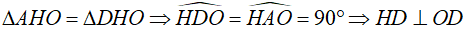
Suy ra HD là tiếp tuyến của đường tròn (O)
Câu 5:
Phương trình đã cho tương đương
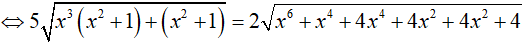
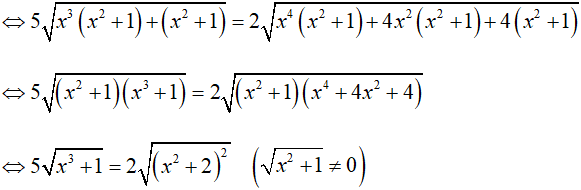
Điều kiện: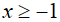 
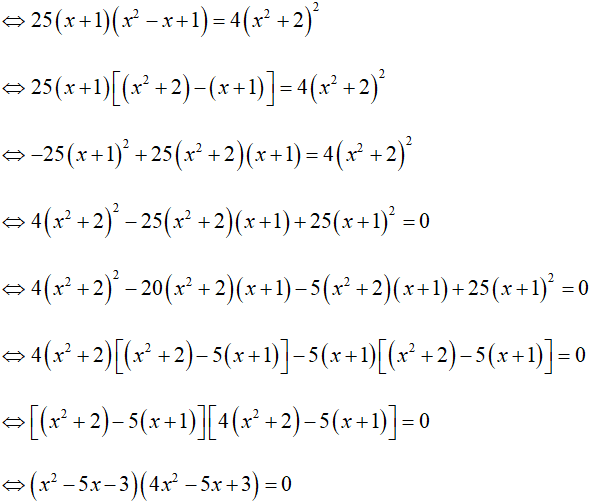
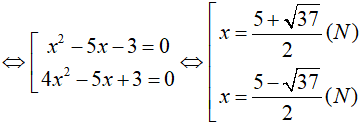
Tập nghiệm của phương trình là: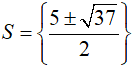 
_______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 10)
I. Trắc nghiệm (1 điểm)
Câu 1: Hệ phương trình 
(với a; b; c; a’; b’; c’ khác 0)
Khi nào hệ có nghiệm duy nhất
A)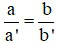 
B) 
C)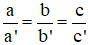 
D)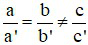 
Câu 2: Một nghiệm của phương trình x + 3y = 5 là
A) (1; 2)
B) (2; 3)
C) (2; 1)
D) (4; 1)
Câu 3: Khẳng định nào sau đây đúng
A) Góc ở tâm có số đo bằng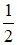 
số đo cung bị chắn
B) Góc nội tiếp có số đo bằng với số đo cung bị chắn
C) Góc có đỉnh nằm bên ngoài đường tròn có số đo bằng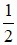 
tổng số đo hai cung bị chắn.
D) Góc tạo bởi tiếp tuyến và dây cung có số đo bằng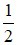 
số đo cung bị chắn
Câu 4: Gọi l là độ dài cung ; bán kính đường tròn là R; số đo cung là n (độ). Đọ dài cung là:
A)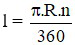 
B)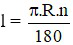 
C)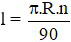 
D)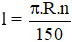 
II. Tự luận
Bài 1 (1,5 điểm): Cho hệ phương trình: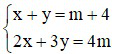 
(m là tham số)
a) Giải hệ phương trình khi m = 1
b) Tìm hệ thức liên hệ giữa x và y không phụ thuộc vào m.
Bài 2 (1,5 điểm): Cho hàm số y = 0,2x2 và y = x.
a) Vẽ hai đồ thị của những hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của hai đồ thị.
Bài 3 (2 điểm): Một ô tô dự định đi từ A đến B trong một khoảng thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn 10km thì đến sớm hơn dự định 3h. Nếu mỗi giờ xe chạy chậm hơn dự định 10km thì đến nơi chậm mất 5h. Tính vận tốc xe lúc đầu và thời gian dự định đi trên quãng đường AB.
Bài 4 (3,5 điểm): Cho đường tròn (O; R) và một điểm A ngoài đường tròn (O) sao cho OA = 3R. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm).
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc với BC
b) Từ B vẽ đường thẳng song song với AC cắt đường tròn tâm (O) tại D (D khác B), AD cắt đường tròn (O) tại E (E khác D). Tính tích AD.AE theo R.
c) Tia BE cắt AC tại F. Chứng minh F là trung điểm AC.
d) Tính theo R diện tích tam giác BDC.
Bài 5 (0,5 điểm): Tìm giá trị nhỏ nhất của biểu thức: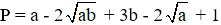 
Đáp án đề thi Giữa học kì 2 môn Toán 9 - Đề số 10
I. Trắc nghiệm (1 điểm)
Câu 1: Hệ phương trình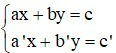 
(với a; b; c; a’; b’; c’ khác 0)
Khi nào hệ có nghiệm duy nhất
A)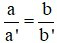 
B)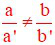 
C)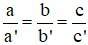 
D)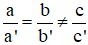 
Lời giải:
Hệ có nghiệm duy nhất khi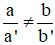 
Câu 2: Một nghiệm của phương trình x + 3y = 5 là
A) (1; 2)
B) (2; 3)
C) (2; 1)
D) (4; 1)
Lời giải:
Ta có 2 + 3.1 = 5 nên (2; 1) là 1 nghiệm của phương trình x + 3y = 5
Câu 3: Khẳng định nào sau đây đúng
A) Góc ở tâm có số đo bằng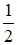 
số đo cung bị chắn
B) Góc nội tiếp có số đo bằng với số đo cung bị chắn
C) Góc có đỉnh nằm bên ngoài đường tròn có số đo bằng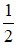 
tổng số đo hai cung bị chắn.
D) Góc tạo bởi tiếp tuyến và dây cung có số đo bằng 
số đo cung bị chắn.
Lời giải:
A) Sai vì góc ở tâm có số đo bằng số đo cung bị chắn
B) Sai vì góc nội tiếp có số đo bằng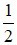 
số đo cung bị chắn
C) Sai vì góc có đỉnh nằm bên ngoài đường tròn có số đo bằng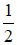 
hiệu số đo hai cung bị chắn.
D) Đúng vì góc tạo bởi tiếp tuyến và dây cung có số đo bằng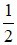 
số đo cung bị chắn.
Câu 4: Gọi l là độ dài cung tròn α; bán kính đường tròn là R; số đo cung α là n (độ). Đọ dài cung α là :
A)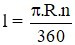 
B)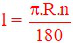 
C)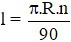 
D)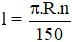 
Lời giải:
Công thức tính độ dài cung tròn là:
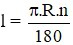
II. Tự luận
Bài 1:
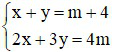
a) Thay m = 1 vào hệ ta có: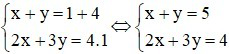 
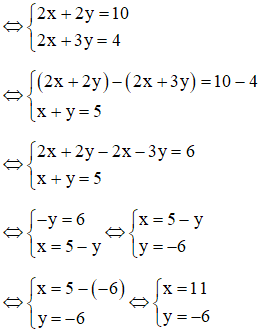
Vậy khi m = 1 thì hệ phương trình đã cho có nghiệm (x; y) = (11; -6)
b)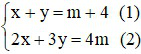 
Từ (1) ta có: m = x + y – 4 thay vào (2) ta được:
2x + 3y = 4(x + y – 4)
⇔ 2x + 3y = 4x + 4y – 16
⇔ 4x +4y – 16 – 2x – 3y = 0
⇔ 2x + y – 16 = 0
Vậy hệ thức liên hệ giữa x và y không phụ thuộc vào tham số m là 2x + y – 16 = 0.
Bài 2:
a) Đồ thị hàm số y = 0,2x2
Bảng giá trị
|
x |
–5 |
–3 |
0 |
3 |
5 |
|
y = 0,2x2 |
5 |
1,8 |
0 |
1,8 |
5 |
Đồ thị hàm số y = x đi qua gốc tọa độ O và điểm (1;1).
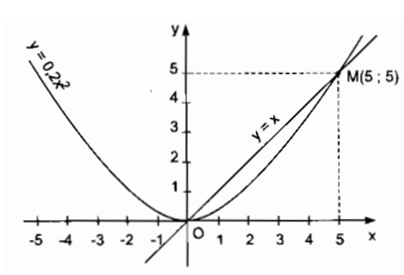
b) Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
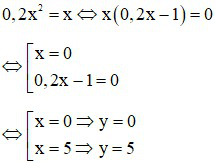
Đồ thị của hai hàm số cắt nhau tại 2 điểm: O (0; 0) và M (5; 5).
Bài 3:
Gọi vận tốc dự định của ô tô là x (km/h) (x > 10)
Gọi thời gian dự định của ô tô là y (h) (y > 3)
Quãng đường AB là: S = xy (km) (1)
Nếu mỗi giờ ô tô tăng vận tốc 10 km/h thì vận tốc lúc đó là x + 10 (km/h)
Vì ô tô đến sớm hơn 3h nên thời gian đi hết quãng đường AB là y – 3 (h)
Quãng đường AB là: S = (x + 1)(y – 3) (km) (2)
Từ (1) và (2) ta có phương trình:
xy = (x + 10)(y – 3)
⇔ xy = xy – 3x + 10y – 30
⇔ 3x – 10y = –30 (*)
Nếu mỗi giờ ô tô giảm vận tốc đi 10 km/h thì vận tốc lúc đó là x – 10 (km/h)
Vì ô tô đến muộn hơn 5h nên thời gian đi hết quãng đường AB là y + 5 (h)
Quang đường AB là: (x – 10)(y + 5) (km) (3)
Từ (1) và (3) ta có phương trình:
xy = (x – 10)(y + 5)
⇔ xy = xy + 5x – 10y – 50
⇔ 5x – 10y = 50 (**)
Từ (*) và (**) ta có hệ phương trình
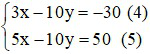
Lấy (5) – (4) ta được:
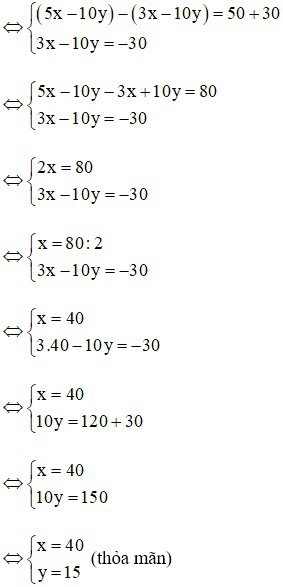
Vậy vận tốc dự định của ô tô là 40 km/h và thời gian dự định của ô tô đi hết quãng đường AB là 15h.
Bài 4:
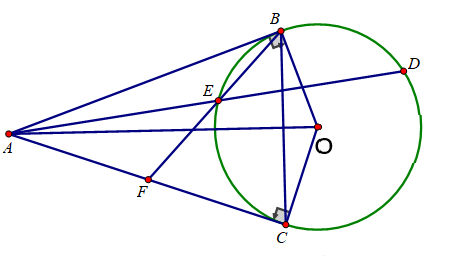
a) Vì AB và AC là hai tiếp tuyến của đường tròn tâm O nên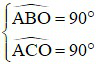 
Xét tứ giác OBAC có:
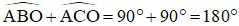
Vậy tứ giác OBAC nội tiếp (dấu hiệu nhận biết)
Chứng minh OA⊥BC
Vì OB = OC = R nên O cách đều hai điểm B và C nên O thuộc đường trung trực của BC
Vì AB = AC (tính chất hai tiếp tuyến cắt nhau) nên A cách đều B và C nên A thuộc đường trung trực của BC
Do đó OA là đường trung trực của BC.
Nên OA là trung trục của BC.
b) Xét ABE và ADB có:
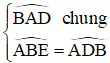
⇒ ΔABE đồng dạng với ΔADB (g – g)
⇒ 
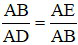hay AD.AE = AB2
Mặt khác ΔABO vuông tại B (cmt)
⇒ 
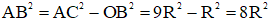
⇒ AB = 2R√2
Vậy AD.AE = 8R2
c) Chứng minh F là trung điểm của AC
Tương tự câu b) ta có FC2 = EF.FB (1)
Mặt khác BD // AC nên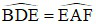 
(so le trong)
Mà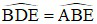 
(cmt) ⇒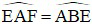 
Xét ΔAFE và ΔBFA có: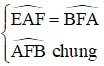 
⇒ ΔAFE đồng dạng với ΔBFA
⇒ 
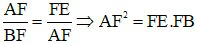(2)
Từ (1) và (2): FC2 = FA2 FC = FA
Vậy F là trung điểm của AC.
d) Do BD // AC và OC⊥AC nên OC⊥BD tại K và K là trung điểm BD (đường kính vuông góc với dây)
Xét ΔCKB và ABO có:
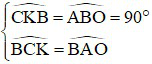
Cho nên ΔCKB đồng dạng với ΔABO, từ đó:
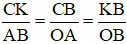(3)
ABO vuông tại B, có BH là đường cao:
BH.OA = OB.AB = R.2R√2 = 2R2√2
Do đó: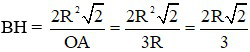 
⇒ 
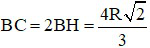(4)
Từ (3) và (4):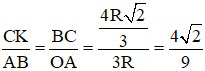 
⇒ 
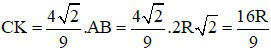
Cũng từ (3) và (4):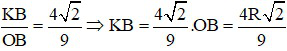 
Từ đó: BD = 2KB =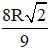 
Vậy diện tích tam giác BDC:
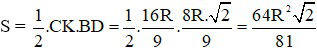(dvdt)
Bài 5:
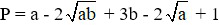
Ta có:
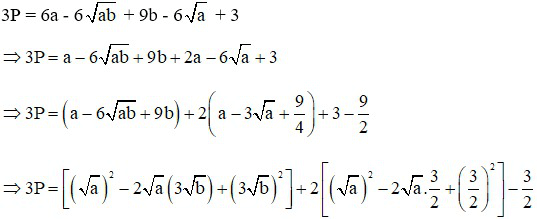
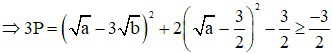với mọi a, b ≥ 0 ⇒ 
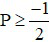với mọi a, b ≥ 0.
Dấu “=” xảy ra ⇔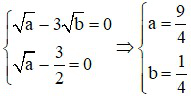 
(thỏa mãn điều kiện)
Vậy Pmin =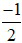 
đạt được ⇔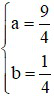 
_______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 11)
Bài 1 (2 điểm): Cho biểu thức:
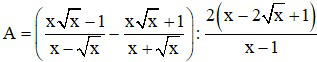
Điều kiên x > 0 và x ≠ 1
a) Rút gọn A.
b) Tìm x để A < 0
Bài 2 (2 điểm): Cho hệ phương trình với m là tham số
(*)
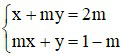a) Tìm m để hệ phương trình đã cho có nghiệm duy nhất. Tìm nghiệm duy nhất đó.
b) Tìm m để hệ phương trình đã cho vô nghiệm.
Bài 3 (2 điểm): Hai bạn An và Khoa cùng làm chung một công việc sau 6 giờ thì xong. Biết nếu làm một mình xong công việc thì Khoa làm lâu hơn An 9 giờ. Tính thời gian làm một mình xong công việc của An, Khoa.
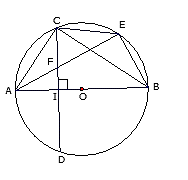
Bài 4 (3,5 điểm): Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I (I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC ( E khác B và C), AE cắt CD tại F. Chứng minh:
a) BEFI là tứ giác nội tiếp đường tròn.
b) AE.AF = AC2.
c) Khi E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp ∆CEF luôn thuộc một đường thẳng cố định.
Bài 5 (0,5 điểm): Cho hai số dương a, b thỏa mãn: a + b ≤ 2√2 . Tìm giá trị nhỏ nhất của biểu thức: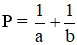 
.
Đáp án đề thi Giữa học kì 2 môn Toán 9 - Đề số 11
Bài 1:
a)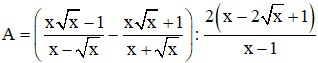 
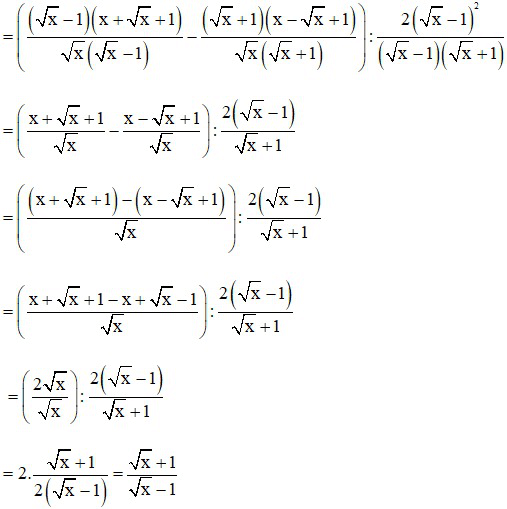
b) Để A < 0 thì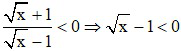 
(do √x + 1 với mọi x)
⇔ √x < 1 ⇔ x < 1. Kết hợp với điều kiện ban đầu 0 < x < 1
Bài 2:
a)
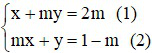
Từ (1) ta có: x = 2m – my thay vào (2) ta được:
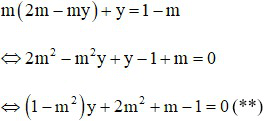
Để hệ (*) có nghiệm duy nhất thì phương trình (**) phải có nghiệm duy nhất.
(**) có nghiệm duy nhất ⇔ 1 – m2 ≠ 0
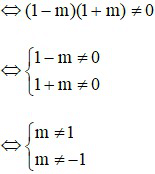
Khi đó: (1 – m2)y = –2m2 – m + 1
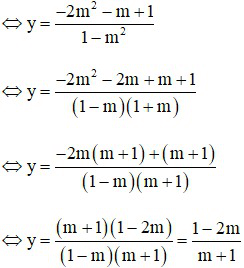
Vì x = 2m – my
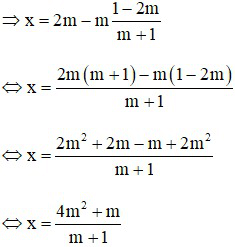
Hệ phương trình có nghiêm duy nhất khi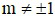 
và chỉ khi và nghiệm duy nhất đó là 
.
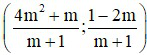b) Để hệ (*) vô nghiệm thì phương trình (**) phải vô nghiệm.
(**) vô nghiệm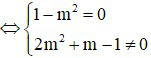 
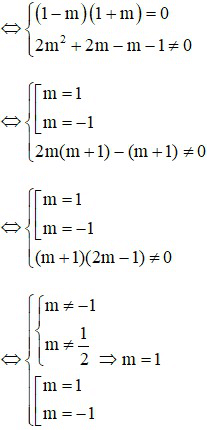
Vậy m = 1 thì hệ phương trình vô nghiệm.
Bài 3:
Gọi thời gian An làm một mình xong công việc là x (h); thời gian Khoa làm một mình xong công việc là y (h) (y > x > 9)
Vì Khoa làm một mình xong công việc lâu hơn An là 9h nên ta có phương trình: y – x = 9 (1)
1h An làm được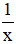 
(công việc)
1h Khoa làm được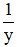 
(công việc)
Vì cả hai bạn cùng làm thì sau 6 giờ xong công việc nên ta có phương trình:
⇔ 
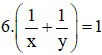
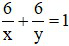(2)
Từ (1) và (2) ta có hệ phương trình:
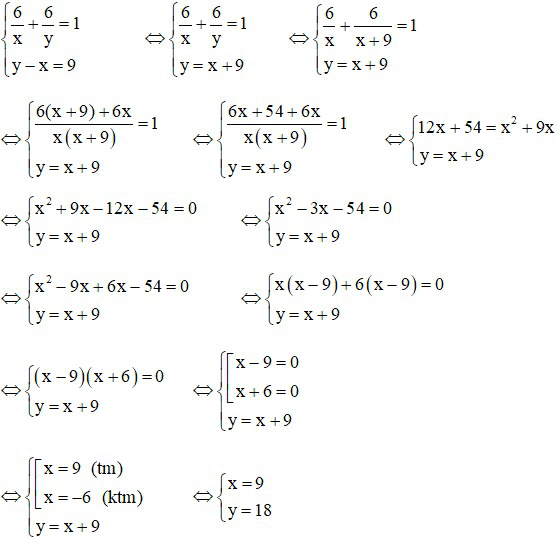
Vậy An làm một mình thì 9h xong công việc; Khoa làm một mình thì 18h xong công việc.
Bài 4:
a) Tứ giác BEFI có: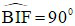 
(gt)
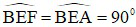(góc nội tiếp chắn nửa đường tròn)
Do đó: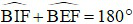 
Suy ra tứ giác BEFI nội tiếp đường tròn đường kính BF
b) Vì AB ⊥ CD nên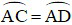 
,
suy ra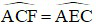 
(góc nội tiếp chắn các cung bằng nhau thì bằng nhau)
Xét ∆ACF và ∆AEC có
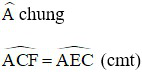
Suy ra: ∆ACF đồng dạng với ∆AEC (g – g)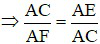 
⇒ AE.AF = AC2
c) Theo câu b) ta có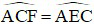 
, suy ra AC là tiếp tuyến của đường tròn ngoại tiếp ∆CEF (1).
Mặt khác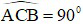 
(góc nội tiếp chắn nửa đường tròn), suy ra AC ⊥ CB (2). Từ (1) và (2) suy ra CB chứa đường kính của đường tròn ngoại tiếp ∆CEF, mà CB cố định nên tâm của đường tròn ngoại tiếp ∆CEF thuộc CB cố định khi E thay đổi trên cung nhỏ BC.
Bài 5:
Ta có (a + b)2 – 4ab = (a – b)2 ≥ 0 ⇒ (a + b)2 ≥ 4ab
⇔ 
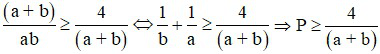, mà a + b ≤ 2√2
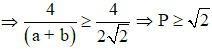. Dấu “ = ” xảy ra 
.
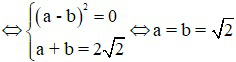Vậy: min P = √2.
_______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 12)
Bài 1 (2 điểm): Giải các phương trình và hệ phương trình sau:
a) x2 – 5x + 6 = 0
b)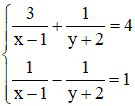 
Bài 2 (2 điểm): Hai vòi nước cùng chảy vào bể thì sau 4 giờ 48 phút đầy bể. Nếu vòi thứ nhất chảy trong 4 giờ vòi hai chảy trong 3 giờ thì được 75% bể. Tính thời gian mỗi vòi chảy một mình đầy bể.
Bài 3 (2 điểm): Cho hàm số y = ax2.
a) Xác định hệ số a biết rằng đồ thị của nó cắt đường thẳng y = –2x + 3 tại điểm A có hoành độ bằng 1.
b) Vẽ đồ thị của hàm số y = –2x + 3 và của hàm số y = ax2 với giá trị của a vừa tìm được trong câu a) trên cùng một mặt phẳng tọa độ.
Bài 4 (3, 5 điểm): Cho tam giác ABC vuông tại A, M là một điểm thuộc cạnh AC (M khác A và C ). Đường tròn đường kính MC cắt BC tại N và cắt tia BM tại I. Chứng minh rằng :
a) ABNM và ABCI là các tứ giác nội tiếp đường tròn.
b) NM là tia phân giác của góc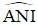 
.
c) BM.BI + CM.CA = AB2 + AC2.
Bài 5 (0,5 điểm): Cho các số a, b, c ∈ [0; 1]. Chứng minh rằng: a + b2 + c3 – ab – bc – ca ≤ 1.
Đáp án đề thi Giữa học kì 2 môn Toán 9 - Đề số 12
Bài 1:
a) x2 – 5x + 6 = 0
Δ = b2 – 4ac = (–5)2 – 4.1.6 = 25 – 24 = 1 > 0
Phương trình có hai nghiệm phân biệt
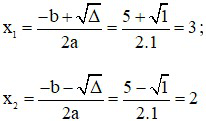
Vậy tập nghiệm của phương trình S = {2; 3}
b)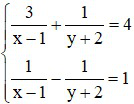 
với x ≠ 1; y ≠ –2
Đặt: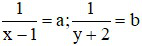 
khi đó hệ phương trình trở thành
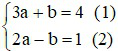
Lấy (1) + (2) ta được:
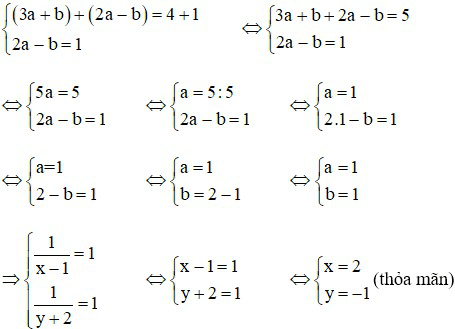
Vậy hệ phương trình đã cho có nghiệm (x; y) là (1; –1).
Bài 2:
Gọi thời gian vòi thứ nhất chảy một mình đầy bể là x (h); vòi thứ hai chảy một mình đầy bể là y (h) (x; y > 0).
Một giờ vòi thứ nhất sẽ chảy được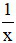 
(bể)
Một giờ vòi thứ hai sẽ chảy được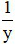 
(bể)
Đổi 4h 48’ = 4,8h
75% =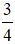 
h
Vì hai vòi chảy trong 4,8h thì đầy bể nên ta có phương trình:
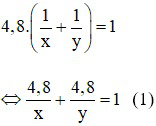
Vì vòi thứ nhất chảy trong 4h; vòi thứ hai chảy trong 3h thì được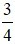 
(bể) nên ta có phương trình:
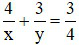(2)
Thừ (1) và (2) ta có hệ phương trình:
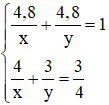
Đặt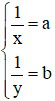 
khi đó hệ trở thành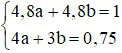 
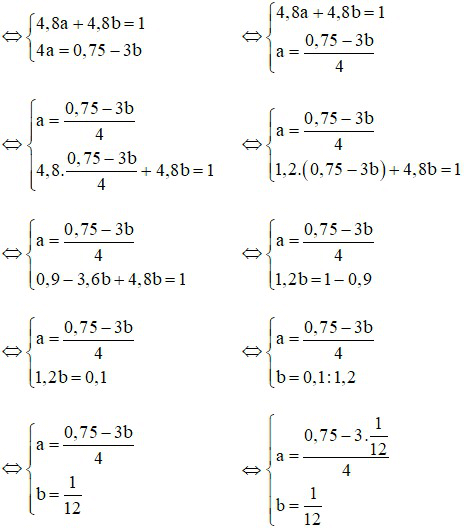
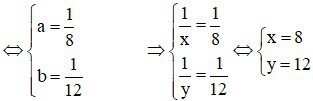(thỏa mãn)
Vậy vòi thứ nhất chảy một mình thì sau 8h sẽ đầy bể; vòi thứ hai chảy một mình thì sau 12h sẽ đầy bể.
Bài 3:
a) Điểm A thuộc đồ thị hàm số y = –2x + 3 nên tọa độ A nghiệm đúng phương trình đường thẳng.
Ta có: y = –2.1 + 3 = 1
Vậy điểm A (1; 1)
Điểm A (1; 1) thuộc đồ thị hàm số y = ax2 nên tọa độ A nghiệm đúng phương trình parabol.
Ta có: 1 = a.12 ⇔ a = 1
Vậy hàm số đã cho là y = x2
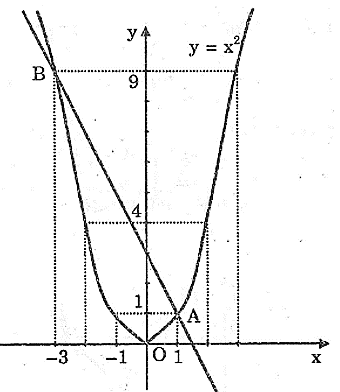
b) Vẽ đồ thị hàm số y = x2
Các giá trị của x và y:
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
|
y = x2 |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
Vẽ đồ thị hàm số y = –2x + 3
Cho x = 0 thì y = 3 ⇒ (0; 3)
Cho y = 0 thì x = 1,5 ⇒ (1,5; 0)
Bài 4:
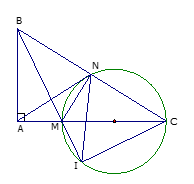
a) Xét tứ giác ABNM ta có:
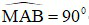(gt)(1).
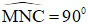(góc nội tiếp chắn nửa đường tròn) 
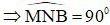(2)
Từ (1) và (2) suy ra ABNM là tứ giác nội tiếp (tổng hai góc đối bằng 180o)
Xét tứ giác ABCI có: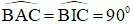 
Mà hai góc này cùng nhìn cạnh BC
⇒ ABCI là tứ giác nội tiếp đường tròn.
b) Tứ giác ABNM nội tiếp suy ra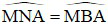 
(góc nội tiếp cùng chắn cung AM) (3).
Tứ giác MNCI nội tiếp suy ra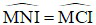 
(góc nội tiếp cùng chắn cung MI) (4).
Tứ giác ABCI nội tiếp suy ra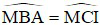 
(góc nội tiếp cùng chắn cung AI) (5).
Từ (3), (4), (5) suy ra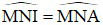 
⇒ NM là tia phân giác của .
c) ∆BNM và ∆BIC có chung góc B và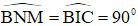 
⇒ ∆BNM đồng dạng với ∆BIC (g - g) ⇒
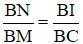⇒ BM.BI = BN.BC .
Tương tự ta có: CM.CA = CN.CB.
Suy ra: BM.BI + CM.CA = BC2 (6).
Áp dụng định lí Pitago cho tam giác ABC vuông tại A ta có:
BC2 = AB2 + AC2 (7).
Từ (6) và (7) suy ra điều phải chứng minh.
Bài 5:
Vì b, c ∈ [0; 1] nên suy ra b2 ≤ b; c3 ≤ c. Do đó:
a + b2 + c3 – ab – bc – ca ≤ a + b + c – ab – bc – ca (1).
Lại có: a + b + c – ab – bc – ca = (a – 1)(b – 1)(c – 1) – abc + 1 (2)
Vì a, b, c ∈ [0; 1] nên (a – 1)(b – 1)(c – 1) ≤ 0 ; –abc ≤ 0
Do đó từ (2) suy ra: a + b + c – ab – bc – ca ≤ 1 (3).
Từ (1) và (3) suy ra: a + b2 + c3 – ab – bc – ca ≤ 1.
_______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 13)
I. Trắc nghiệm (1 điểm)
Câu 1: Hệ phương trình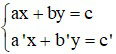 
(với a; b; c; a’; b’; c’ khác 0)
Khi nào hệ vô nghiệm
A)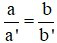 
B)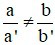 
C)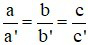 
D)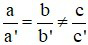 
Câu 2: Một nghiệm của phương trình 2x + 3y = 1 là
A) (–1; 2)
B) (2; –3)
C) (2; –1)
D) (4; 1)
Câu 3: Khẳng định nào sau đây sai
A) Góc ở tâm có số đo bằng số đo cung bị chắn
B) Góc nội tiếp có số đo bằng với số đo cung bị chắn
C) Góc có đỉnh nằm bên ngoài đường tròn có số đo bằng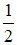 
hiệu số đo hai cung bị chắn.
D) Góc tạo bởi tiếp tuyến và dây cung có số đo bằng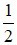 
số đo cung bị chắn
Câu 4: Gọi l là độ dài cung α; bán kính đường tròn là R; số đo cung α là n (độ). Đọ dài cung α là:
A)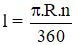 
B)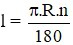 
C)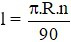 
D)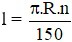 
II. Tự luận
Bài 1 (2 điểm): Cho biểu thức: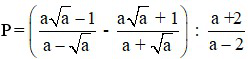 
với a > 0, a ≠ 1, a ≠ 2.
a) Rút gọn P.
b) Tìm giá trị nguyên của a để P có giá trị nguyên
Bài 2 (2 điểm):
a) Tìm tọa độ giao điểm của đường thẳng d: y = –x + 2 và Parabol (P): y = x2.
b) Cho hệ phương trình: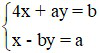 
.
Tìm a và b để hệ đã cho có nghiệm duy nhất (x; y) = (2; –1).
Bài 3 (2 điểm): Một khu vườn hình chữ nhật có chu vi bằng 60m. Nếu tăng chiều dài lên 4 lần và chiều rộng lên 3 lần thì chu vi khu vườn sẽ tăng 162m. Tìm diện tích khi vườn.
Bài 4 (3,5 điểm): Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho AI =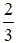 
AO. Kẻ dây MN vuông góc với AB tại I, gọi C là điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và B. Nối AC cắt MN tại E.
a) Chứng minh tứ giác IECB nội tiếp .
b) Chứng minh hệ thức: AM2 = AE.AC.
c) Hãy xác định vị trí của điểm C sao cho khoảng cách từ N đến tâm đường tròn ngoại tiếp tam giác CME là nhỏ nhất.
Bài 5 (0,5 điểm): Cho x và y là hai số thỏa mãn đồng thời : x ≥ 0, y ≥ 0, 2x + 3y ≤ 6 và 2x + y ≤ 4.
Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức K = x2 – 2x – y.
Đáp án đề thi Giữa học kì 2 môn Toán 9 - Đề số 13
I. Trắc nghiệm (1 điểm)
Câu 1: Hệ phương trình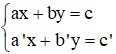 
(với a; b; c; a’; b’; c’ khác 0)
Khi nào hệ vô nghiệm
A)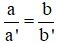 
B)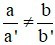 
C)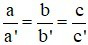 
D)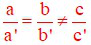 
Lời giải
Hệ vô nghiệm khi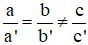 
Câu 2: Một nghiệm của phương trình 2x + 3y = 1 là
A) (-1; 2)
B) (2; -3)
C) (2; -1)
D) (4; 1)
Lời giải:
Ta có: 2.2 + 3.(-1) = 4 – 3 = 1. Vậy (2; -1) là nghiệm của phương trình 2x + 3y = 1
Câu 3: Khẳng định nào sau đây sai
A) Góc ở tâm có số đo bằng số đo cung bị chắn
B) Góc nội tiếp có số đo bằng với số đo cung bị chắn
C) Góc có đỉnh nằm bên ngoài đường tròn có số đo bằng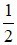 
hiệu số đo hai cung bị chắn.
D) Góc tạo bởi tiếp tuyến và dây cung có số đo bằng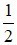 
số đo cung bị chắn
Lời giải:
B sai vì Góc nội tiếp có số đo bằng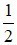 
số đo cung bị chắn
Câu 4: Công thức tính độ dài cung tròn là:
A)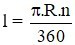 
B)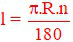 
C)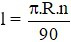
D)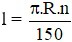
Lời giải:
Công thức tính độ dài cung tròn là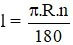 
II. Tự luận
Bài 1:
1) Điều kiện: a ≥ 0, a ≠ 1, a ≠ 2
Ta có: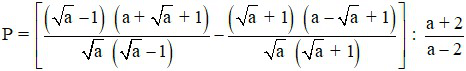 
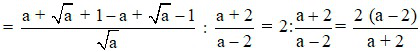
2) Ta có: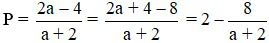 
P nhận giá trị nguyên khi và chỉ khi 8 ⋮ (a + 2)
Bài 2:
a) Hoành độ giao điểm của đường thẳng (d) và Parabol (P) là nghiệm của phương trình:
–x + 2 = x2 ⇔ x2 + x – 2 = 0.
Có a = 1; b = 1; c = –2 nên a + b + c = 0
Phương trình này có tổng các hệ số bằng 0 nên có 2 nghiệm là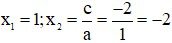 
+ Với x = 1 thì y = 1, ta có giao điểm thứ nhất là (1;1)
+ Với x = -2 thì y = 4, ta có giao điểm thứ hai là (–2; 4)
Vậy (d) giao với (P) tại 2 điểm có tọa độ là (1; 1) và (–2; 4)
b) Thay x = 2 và y = –1 vào hệ đã cho ta được:
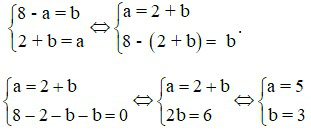
Thử lại : Thay a = 5 và b = 3 vào hệ đã cho thì hệ có nghiệm duy nhất (2; –1).
Vậy a = 5; b = 3 thì hệ đã cho có nghiệm duy nhất (2; –1).
Bài 3:
Gọi chiều dài của khu vườn là x (m); chiều rộng của khu vườn là y (m) (x > y > 0)
Vì chu vi khu vườn là 60m nên ta có phương trình:
2.(x + y) = 60
⇔ x + y = 60:2
⇔ x + y = 30 (1)
Nếu tăng chiều dài lên 4 lần thì chiều dài mới là 4x (m); nếu tăng chiều rộng lên 3 lần thì chiều rộng mới là 3y (m).
Chu vi khu vườn mới là: 2(4x + 3y) = 8x + 6y (m)
Vì chu vi khu vườn mới hơn chu vi khu vườn cũ 162m nên ta có phương trình:
(8x + 6y) – 2(x + y) = 162
⇔ 8x + 6y – 2x – 2y = 162
⇔ 6x + 4y = 162 (2)
Từ (1) và (2) ta có hệ phương trình:
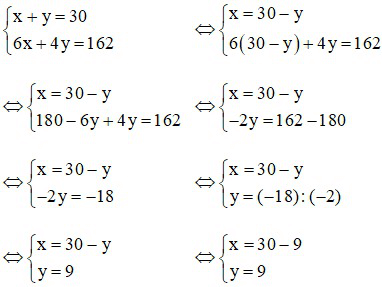
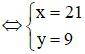(thỏa mãn)
Diện tích khu vườn ban đầu là:
S = 21.9 = 189 m2
Bài 4:
a) Theo giả thiết MN ⊥ AB tại I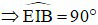 
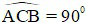hay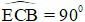 
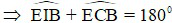
mà đây là hai góc đối của tứ giác IECB nên tứ giác IECB là tứ giác nội tiếp.
b) Theo giả thiết MN ⊥ AB, suy ra A là điểm chính giữa của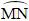 
nên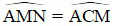 
(hai góc nội tiếp chắn hai cung bằng nhau) hay 
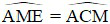, lại có 
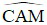là góc chung do đó tam giác AME đồng dạng với tam giác ACM
⇒ 
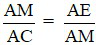
⇒ AM2 = AE.AC.
c) Theo trên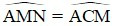 
⇒ AM là tiếp tuyến của đường tròn ngoại tiếp ΔECM. Nối MB ta có = 900, do đó tâm O1 của đường tròn ngoại tiếp ΔECM phải nằm trên BM.
Ta thấy NO1 nhỏ nhất khi NO1 là khoảng cách từ N đến BM ⇒ NO1 ⊥ BM. Gọi O1 là chân đường vuông góc kẻ từ N đến BM ta được O1 là tâm đường tròn ngoại tiếp ΔECM có bán kính là O1M.
Do đó để khoảng cách từ N đến tâm đường tròn ngoại tiếp ΔECM là nhỏ nhất thì C phải là giao điểm của đường tròn (O1), bán kính O1M với đường tròn (O) trong đó O1 là hình chiếu vuông góc của N trên BM.
Bài 5:
Từ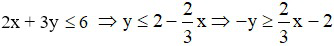 
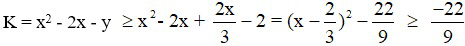
Suy ra : min K =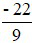 
khi x = 
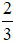; y =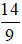 
Ta có : 2x2 + xy ≤ 4x (x ≥ 0)
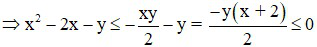
Suy ra: max K = 0 khi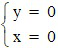 
hoặc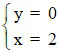 
_______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 14)
Bài 1 (2 điểm): Cho biểu các biểu thức:
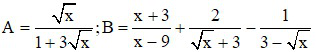với x > 0; x 9.
a) Tính A khi x =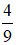 
b) Rút gọn B
c) Cho P = B: A. Tìm x để P < 3
Bài 2 (2 điểm): Cho hệ phương trình với m là tham số
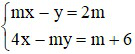(I)
Tìm điều kiện của m để hệ phương trình có nghiệm.
Bài 3 (2 điểm): Hai xí nghiệp tổng cộng phải làm 360 dụng cụ. Trên thực tế xí nghiệp I vượt mức 12%, xí nghiệp II vượt mức 10% nên tổng dụng cụ làm được là 400 dụng cụ. Tính số dụng cụ mỗi xí nghiệp phải làm so với dự định.
Bài 4 (3, 5 điểm): Trên đường tròn (O) đường kính AB, lấy điểm D (D khác A; D khác B). Gọi E là điểm chính giữa cung nhỏ BD. Lấy điểm C trên đoạn thẳng AB (C khác A và C khác B). Đường thẳng CE cắt đường tròn (O) tại điểm thứ hai là F. GỌi G là giao điểm của AE và DF.
a) Chứng minh: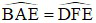 
và AGCF là tứ giác nội tiếp.
b) Chứng minh CG vuông góc với AD.
c) Kẻ đường thẳng đi qua C, song song với AD và cắt DF tại H. Chứng minh CH = CB.
Bài 5 (0,5 điểm): Cho x, y, z là các số thực thỏa mãn: x + y + x = 1
Tìm giá trị nhỏ nhất của biểu thức: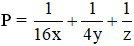 
Đáp án đề thi Giữa kì 2 môn Toán 9 - Đề số 14
Bài 1:
a) Thay x =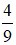 
(thảo mãn điều kiện) vào A ta được
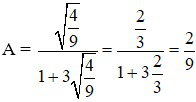
b)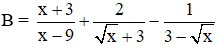 
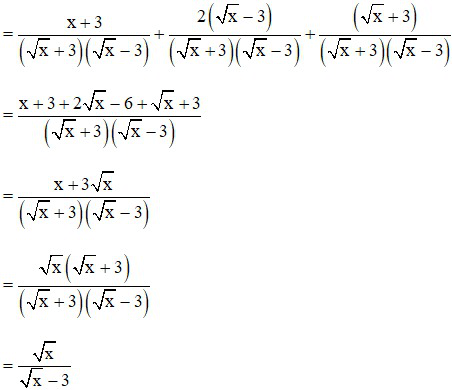
c) Ta có:
P = B : A =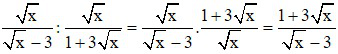 
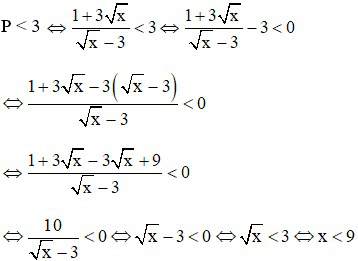
Kết hợp với điều kiện đề bài thì để P < 3 thì 0 < x < 9
Bài 2:
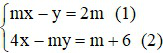
Từ phương trình (1) ta có:
y = mx – 2m thay vào phương trình (2) ta có:
4x – m(mx – 2m) = m + 6
⇔ 4x – m2x + 2m2 = m + 6
⇔ (4 – m2)x + 2m2 – m – 6 = 0 (II)
Để hệ phương trình (I) có nghiệm thì phương trình (II) phải có nghiệm.
Để phương trình (II) có nghiệm ta có hai trường hợp sau:
Trường hợp 1: (II) có nghiệm duy nhất
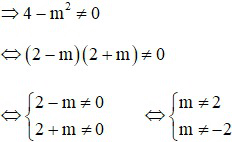
Trường hợp 2: Phương trình (II) có vô số nghiệm
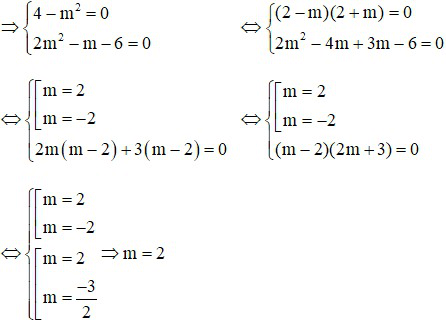
Kết hợp hai trường hợp ta được m ≠ –2 thì hệ phương trình luôn có nghiệm.
Bài 3:
Gọi số dụng cụ xí nghiệp I phải làm là x (dụng cụ) (x > 0; x ∈ N*)
Gọi số dụng cụ xí nghiệp II phải làm là y (dụng cụ) (y > 0; x ∈ N*)
Vì ban đầu cả hai xí nghiệp phải làm 360 dụng cụ nên ta có phương trình:
x + y = 360 (1)
Vì xí nghiệp I vớt mức 12% nên số dụng cụ thực tế xí nghiệp I làm được là: (100 + 12)%x = 112%x = 1,12x
Vì xí nghiệp II vượt mức 10 % nên số dụng cụ thực tế xí nghiệp II làm được là: (100 + 10)%y = 110%y = 1,1y.
Thực tế cả hai xí nghiệp đã làm được 400 dụng cụ nên ta có phương trình:
1,12x + 1,1y = 400 (2)
Từ (1) và (2) ta có hệ phương trình:
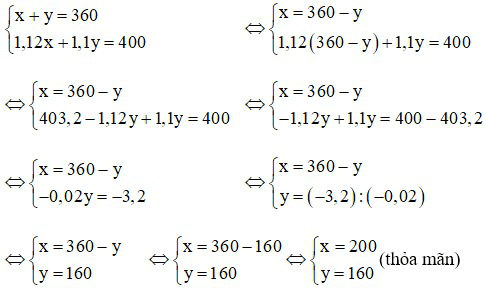
Vậy số dụng cụ xí nghiệp I cần làm theo kế hoạch là 200 dụng cụ; số dụng cụ xí nghiệp II cần làm theo kế hoạch là 160 dụng cụ.
Bài 4:
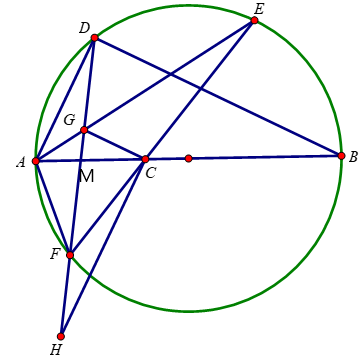
a) Xét đường tròn (O), ta có:
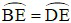(E là điểm chính giữa cung BD)
⇒
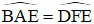(2 góc nội tiếp chắn hai cung bằng nhau)
Xét tứ giác AGCF có:
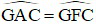(cmt)
⇒ 2 đỉnh A và F cùng nhìn cạnh GC dưới hai góc bằng nhau,
⇒ Tứ giác AGCF là tứ giác nội tiếp.
b) Tứ giác AGCF là tứ giác nội tiếp
⇒ 
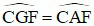(2 góc nội tiếp cùng chắn cung CF)
Mà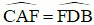 
(hai góc nội tiếp cùng chắn cung FB).
⇒ 
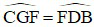
Mà hai góc này ở vị trí đồng vị
Do đó BD // GC
MÀ BD vuông góc với AD (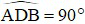
góc nội tiếp chắn nửa đường tròn)
⇒ GC ⊥ AD
c) Gọi M là giao điểm của AB và DF
Do CH // AD nên ta có:
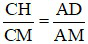(1)
Lại có: AE là phân giác góc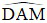 
(do E là điểm chính giữa cung BD) nên AG là phân giác của tam giác AMD
⇒ 
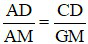(tính chất đường phân giác) (2)
Mặt khác, ta lại có: CG // BD nên:
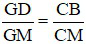(3)
Từ (1); (2); (3) ⇒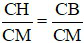 
⇒ CH = CB (điều phải chứng minh)
Bài 5:
Ta có: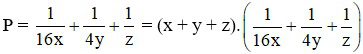 
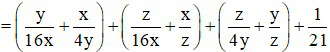
Ta lại có:
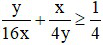(dấu bằng xảy ra khi y = 2x)
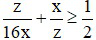(dấu bằng xảy ra khi z = 4x)
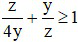(dấu bằng xảy ra khi z = 2y)
Vậy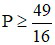 
khi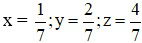 
Vậy giá trị nhỏ nhất của P là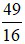 
_______________________________________________________________________
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa học kì 2
Năm học 2022 - 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Đề thi Giữa học kì 2 Toán lớp 9 có đáp án - (Đề số 15)
I. Trắc nghiệm
Câu 1: Tứ giác ABCD nội tiếp được trong một đường tròn. Nếu 
thì số đo 
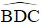là:
A) 110o
B) 70o
C) 160o
D) 140o
Câu 2: Cho phương trình 3x + y = 5. Đâu là một nghiệm của phương trình
A) (2; 3)
B) (1; 2)
C) (-2; 4)
D) (3; 6)
Câu 3: Cho phương trình 2x – y – 5. Phương trình nào sau đây kết hợp với phương trình đã cho để được một hệ phương trình có vô số nghiệm?
A) x – y = 5
B) –6x + 3y = 15
C) 6x + 15 = 3y
D) 6x – 15 = 3y
Câu 4: Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M và tạo thành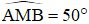 
. Khi đó số đo cung bị chắn bở góc ở tâm AOB là bao nhiêu độ?
A) 50o
B) 40o
C) 130o
D) 80o
II. Tự luận
Bài 1 (2 điểm):
Cho (P) y = x2 và đường thẳng (d): y = 2x – 3
a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của (P) và (d)
Bài 2 (2,5 điểm): Giải bài toán bằng cách lập hệ phương trình:
Hai tổ sản xuất cùng nhận chung một đơn hàng, nếu hai tổ cùng làm thì sau 15 ngày sẽ xong. Tuy nhiên, sau khi cùng làm được 6 ngày thì tổ I có việc bận phải chuyển công tác kasc, tổ II làm một mình 24 ngày nữa mới hoàn thành đơn hàng. Hỏi nếu làm một mình thì mỗi tổ làm xong trong bao nhiêu ngày?
Bài 3 (3,5 điểm):
Cho đường tròn (O; R), dây MN không đi qua tâm, C và D là hai điểm bất kỳ thuộc dây MN (C; D không trùng với M, N). A là điểm chính giữa của cung nhỏ MN. Các đường thẳng AC và AD lần lượt cắt (O) tại điểm thứ hai là E; F.
a) Chứng minh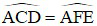 
và tứ giác CDEF nội tiếp.
b) Chứng minh: AM2 = AC.AE
c) Kẻ đường kính AB. Gọi I là tâm đường tròn ngoại tiếp tam giác MCE. Chứng minh M, I, B thẳng hàng.
Bài 4 (1 điểm): Với x, y, z là các số thực dương thỏa mãn đẳng thức xy + yz + zx = 5
Tìm giá trị nhỏ nhất của biểu thức:
