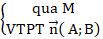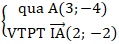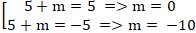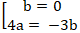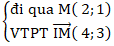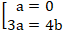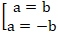Viết phương trình tiếp tuyến của đường tròn tại 1 điểm, đi qua 1 điểm

A. Phương pháp giải

Cho đường tròn ( C) có tâm I( a; b); bán kính R và điểm M( x₀; y₀) :

+ Lập phương trình tiếp tuyến (d) của ( C ) tại điểm M:

Do (d) là tiếp tuyến của đường tròn tại M nên d vuông góc IM

⇒ Đường thẳng ( d) : 

⇒ Phương trình đường thẳng d.

+ Lập phương trình tiếp tuyến (d) của ( C) đi qua M :

- Đường thẳng ( d) : 

⇒ (d): A(x - x₀) + B( y - y₀) = 0.

- Do đường thẳng d là tiếp tuyến của đường tròn ( C) nên d( I; d) = R

⇒ Một phương trình hai ẩn A; B. Giải phương trình ta được A = kB.

- Chọn A= ... ⇒ B=...⇒ Phương trình đường thẳng d.

B. Ví dụ minh họa

Ví dụ 1. Cho đường tròn ( C): (x-1)² + (y + 2)² = 2. Viết phương trình tiếp tuyến d của (C) tại điểm A(3; -4) .

A. d: x + y + 1 = 0    B. d: x - 2y - 11 = 0

C. d: x - y - 7 = 0    D. d: x - y + 7 = 0

Lời giải

+ Đường tròn ( C) có tâm I( 1; -2) .

+ Do đường thẳng d tiếp xúc với đường tròn tại điểm A(3; -4) nên đường thẳng d vuông góc với đường thẳng IA.

+ Phương trình đường thẳng (d): 

⇒ phương trình (d) là: 2( x - 3) – 2( y + 4) = 0

⇔ (d) : 2x - 2y - 14 = 0 hay x - y - 7 = 0

Chọn C.

Ví dụ 2 : Cho đường tròn (x - 3)² + (y + 1)² = 5 . Phương trình tiếp tuyến của ( C) song song với đường thẳng d : 2x + y + 7 = 0 là

A. 2x + y = 0; 2x + y - 10 = 0    B. 2x + y + 1 = 0 ; 2x + y - 1 = 0

C. 2x - y + 1 = 0; 2x + y - 10 = 0    D. 2x + y = 0; x + 2y - 10 = 0

Hướng dẫn:

Do tiếp tuyến cần tìm song song với đường thẳng d: 2x + y + 7 = 0 nên

phương trình tiếp tuyến có dạng ∆: 2x + y + m = 0 với m ≠ 7 .

Đường tròn ( C) có tâm I( 3; -1) và bán kính R = √5

Đường thẳng tiếp xúc với đường tròn ( C) khi :

d( I , ∆) = R ⇔  = √5 ⇔ |5 + m| = 5

⇔ 

Vậy ∆₁ : 2x + y = 0 , ∆₂ : 2x + y - 10 = 0

Chọn A.

Ví dụ 3. Viết phương trình tiếp tuyến ∆ của đường tròn ( C): x² + y² - 4x - 4y + 4 = 0, biết tiếp tuyến đi qua điểm B( 4; 6) .

A. x - 4 = 0 hoặc 3x + 4y - 36 = 0    B. x - 4 = 0 hoặc y - 6 = 0.

C. y - 6 = 0 hoặc 3x + 4y - 36 = 0    D. x - 4 = 0 hoặc 3x - 4y + 12 = 0

Lời giải

+ Đường tròn (C) có tâm I( 2; 2) và bán kính R = 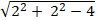 = 2

+ Tiếp tuyến ∆: 

⇒ Phương trình ∆: a(x - 4) + b(y - 6) = 0 hay ax + by - 4a - 6b = 0 (*)

+ Do ∆ là tiếp tuyến của đường tròn ( C) nên d(I; ∆) = R

⇔  = 2 ⇔|- 2a - 4b| = 2

⇔ |a + 2b| =  ⇔ a² + 4ab + 4b² = a² + b²

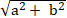
⇔ 4ab + 3b² = 0 ⇔ 

+ Nếu b = 0; chọn a = 1 thay vào (*) ta được ∆: x - 4 = 0.

+ Nếu 4a = - 3b ta chọn a = 3 thì b = -4 thay vào ( *) ta được: 3x - 4y + 12 = 0

Vậy có hai tiếp tuyến thỏa mãn là x - 4 = 0 và 3x - 4y + 12 = 0 .

Chọn D.

Ví dụ 4. Phương trình tiếp tuyến d của đường tròn (C): (x + 2)² + (y + 2)² = 25 tại điểm M(2; 1) là:

A. d: -y + 1 = 0    B. d: 4x + 3y + 14 = 0

C. d: 3x - 4y - 2 = 0    D. d: 4x + 3y - 11 = 0

Lời giải

+ Đường tròn ( C) có tâm I(-2; -2) và bán kính R= 5.

+ Do đường thẳng d tiếp xúc với đường tròn taị điểm M nên hai đường thẳng d và IM vuông góc với nhau.

+ Đường thẳng d: 

⇒Phương trình (d) : 4( x - 2) + 3( y - 1) = 0 hay 4x + 3y - 11 = 0

Chọn D.

Ví dụ 5: Cho đường tròn ( C) có tâm I(1; 3), bán kính R= √52. Lập phương trình tiếp tuyến của đường tròn tại điểm M biết điểm M thuộc đường thẳng d: 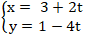 và tọa độ M nguyên?

A. x + 2y + 3 = 0    B. 2x + 5y + 21 = 0

C. 2x - 3y - 19 = 0    D. Đáp án khác

Lời giải

+ Do điểm M thuộc đường thẳng d nên tọa độ M(3 + 2t; 1 - 4t).

+ Do điểm M thuộc đường tròn nên IM = R

⇔ IM² = R² ⇔ ( 2 + 2t)² + ( 2 + 4t)² = 52

⇔ 4t² + 8t + 4 + 16t² + 16t + 4 = 52

⇔ 20t² + 24t – 44 = 0 ⇔ t = 1 hoặc t = 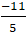 ( loại) .

+ Với t = 1 thì tọa độ M(5; -3) .

⇒ Phương trình tiếp tuyến của đường tròn tại điểm M (5; -3):

(∆) : 

⇒ Phương trình tiếp tuyến : 2( x - 5) – 3(y + 3) = 0 hay 2x - 3y - 19 = 0

Chọn C.

Ví dụ 6. Cho đường tròn (C): (x + 1)² + (y - 1)² = 25 và điểm M(9; -4) . Gọi ∆ là tiếp tuyến của ( C) , biết ∆ đi qua M và không song song với các trục tọa độ. Khi đó khoảng cách từ điểm P(6; 5) đến ∆ bằng:

A. 2    B. 3    C. 4    D. 5

Lời giải

+ Đường tròn (C) có tâm I(-1; 1)và bán kính R= 5.

+ Tiếp tuyến ∆: 

⇒ Phương trình ∆: a(x - 9) + b(y + 4) = 0 hay ax + by – 9a + 4b = 0 (*)

+ Do ∆ là tiếp tuyến của đường tròn ( C) nên d(I; ∆) = R

⇔  = 5 ⇔ |-10a + 5b| = 5

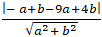
⇔ |-2a + b| = 

⇔ 4a² - 4ab + b² = a² + b² ⇔ 3a² - 4ab = 0

⇔ 

+ Nếu a = 0 chọn b = 1 thay vào (*) ta được: y + 4 = 0 ( loại) vì tiếp tuyến không song song với các trục tọa độ.

+ Nếu 3a = 4b, chọn a = 4 thì b = 3 ta được ∆: 4x + 3y - 24 = 0

⇒ Khoảng cách từ P(6;5) đến đường thẳng ∆ là:

d(P, ∆) = 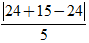 = 3

Chọn B.

Ví dụ 7. Có bao nhiêu đường thẳng đi qua gốc tọa độ O và tiếp xúc với đường tròn
(C): x² + y² - 2x + 4y - 11 = 0?

A. 0.    B. 2.    C. 1.    D. 3.

Lời giải

Đường tròn (C) có tâm I(1; -2) và bán kính R = 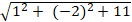 = 4.

Độ dài OI = 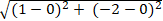 = √5

⇒ Điểm O nằm trong đường tròn nên không có tiếp tuyến nào của đường tròn kẻ từ O.

Chọn A.

Ví dụ 8. Cho đường tròn (C): (x-3)² + (y + 3)² = 1. Qua điểm M(4; -3) có thể kẻ được bao nhiêu đường thẳng tiếp xúc với đường tròn ( C) ?

A. 0.    B. 1.    C. 2.    D. Vô số.

Lời giải

Thay tọa độ điểm M vào phương trình đường tròn( C) ta được :

( 4 - 3)² + (-3 + 3)² = 1

⇒ Điểm M thuộc (C).

⇒ có đúng 1 tiếp tuyến của đường tròn kẻ từ M.

Chọn B.

Ví dụ 9. Có bao nhiêu đường thẳng đi qua điểm N(-2; 0) tiếp xúc với đường tròn
(C): (x - 2)² + (y + 3)² = 4?

A. 0.    B. 1.    C. 2.    D. Vô số.

Lời giải

Đường tròn ( C) có tâm I(2; -3) và bán kính R = 2.

Độ dài IN = 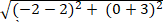 = 5 > R

⇒ Điểm N nằm ngoài đường tròn ( C) nên qua điểm N kẻ được hai tiếp tuyến đến đường tròn (C).

Chọn C.

Ví dụ 10. Viết phương trình tiếp tuyến ∆ của đường tròn ( C): (x - 1)² + (y + 2)² = 8, biết tiếp tuyến đi qua điểm A( 5; -2).

A. x - 5 = 0 .    B. x + y - 3 = 0 hoặc x - y 7 = 0.

C. x- 5= 0 hoặc x + y - 3 = 0 .    D. y + 2 = 0 hoặc x - y - 7 = 0 .

Lời giải

+ Đường tròn (C) có tâm I(1; -2) và bán kính R = 2√2

+ Tiếp tuyến ∆: 

⇒ Phương trình ∆: a( x - 5) + b(y + 2) = 0 hay ax + by - 5a + 2b = 0.

+ Do ∆ là tiếp tuyến của đường tròn ( C) nên d(I; ∆) = R

⇔  = 2√2 ⇔ |- 4a| = 2√2.

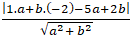
⇔ 16a² = 8( a² + b² ) ⇔ 8a² = 8b²

⇔ 

+ Nếu a = b; ta chọn a = 1 ⇒ b = 1. Khi đó phương trình tiếp tuyến ∆: x + y - 3 = 0

+ Nếu a = - b; chọn a = 1 thì b = - 1. Khi đó phương trình tiếp tuyến ∆: x - y - 7 = 0.

Vậy có hai tiếp tuyến thỏa mãn là x + y - 3 = 0 và x - y - 7 = 0

Chọn B.

Ví dụ 11: Cho đường tròn (C) : (x - 3)² + (y - 1)² = 10. Phương trình tiếp tuyến của (C) tại điểm A( 4; 4) là

A. x - 3y + 8 = 0.    B. x + 3y – 16 = 0.    C. 2x - 3y + 5 = 0 .    D. x + 3y - 16 = 0.

Hướng dẫn giải

Đường tròn (C) có tâm I( 3;1). Gọi d là tiếp tuyến của đường tròn (C) tại điểm A; khi đó d và IA vuông góc với nhau.

⇒ IA→ = (1; 3) là vectơ pháp tuyến của d.

Suy ra phương trình d: 1( x - 4) + 3( y - 4 ) = 0

Hay x + 3y - 16 = 0.

Chọn D.