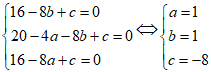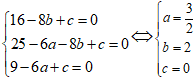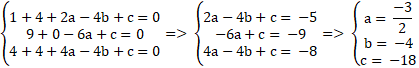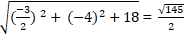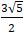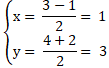Viết phương trình đường tròn đi qua 3 điểm (đường tròn ngoại tiếp tam giác)

A. Phương pháp viết phương trình đường tròn đi qua 3 điểm

Cho đường tròn ( C) đi qua ba điểm A; B và C. Lập phương trình đường tròn đi qua ba điểm:

1/ Bước 1: Gọi phương trình đường tròn là ( C): x² + y² - 2ax - 2by + c = 0 (*)

( với điều kiện a² + b² - c > 0).

2/ Bước 2: Do điểm A; B và C thuộc đường tròn nên thay tọa độ điểm A; B và C vào (*) ta được phương trình ba phương trình ẩn a; b; c.

3/ Bước 3: giải hệ phương trình ba ẩn a; b; c ta được phương trình đường tròn.

B. Ví dụ minh họa

Ví dụ 1: Đường tròn nào dưới đây đi qua 2 điểm A(1 ; 0) ; B( 3 ; 4) ?

A. x² + y² + 8x - 2y - 9 = 0    B. x² + y² - 3x - 16 = 0

C. x² + y² - x + y = 0    D. x² + y² - 4x - 4y + 3 = 0

Hướng dẫn giải

Thay tọa độ hai điểm A và B vào các phương án:

Điểm B( 3; 4) không thuộc đường tròn A.

Điểm A(1; 0) không thuộc đường tròn B.

Điểm B(3; 4) không thuộc đường tròn C.

Điểm A; B cùng thuộc đường tròn D.

Chọn D.

Ví dụ 2. Tìm tọa độ tâm đường tròn đi qua 3 điểm A( 0; 4); B( 2; 4) và C( 4; 0)

A. (0; 0)    B. (1; 0)    C. (3; 2)    D. (1; 1)

Hướng dẫn giải

Phương trình đường tròn (C) có dạng:

x² + y² - 2ax – 2by + c = 0 ( a² + b² –c > 0)

Do 3 điểm A; B; C thuộc (C) nên 

Vậy tâm I( 1; 1)

Chọn D.

Ví dụ 3. Tìm bán kính đường tròn đi qua 3 điểm A(0; 4); B(3; 4); C(3; 0).

A. 5    B. 3    C. √6,25    D. √8

Hướng dẫn giải

Phương trình đường tròn (C) có dạng:

x² + y² - 2ax – 2by + c = 0 ( a² + b² – c > 0)

Do 3 điểm A; B; C thuộc (C) nên 

Vậy bán kính R = 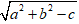 = √6,25.

Chọn C.

Ví dụ 4. Cho tam giác ABC có A(-2; 4); B(5; 5) và C(6; -2). Đường tròn ngoại tiếp tam giác ABC có phương trình là:

A. x² + y² - 2x - y + 20 = 0    B. (x - 2)² + (y - 1)² = 20

C. x² + y² - 4x - 2y + 20 = 0    D. x² + y² - 4x - 2y - 20 = 0

Lời giải

Gọi đường tròn ngoại tiếp tam giác là ( C): x² + y² + 2ax + 2by + c = 0 (a² + b² - c > 0 )

Do ba điểm A; B và C thuộc đường tròn là:

Vậy đường tròn ( C) cần tìm: x² + y² - 4x - 2y - 20 = 0

Chọn D.

Ví dụ 5. Cho tam giác ABC có A(1; -2); B(-3; 0); C(2; -2) . Biết tam giác ABC nội tiếp đường tròn ( C). Tính bán kính đường tròn đó?

A. 5    B. 6    C. 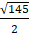    D. √37

Lời giải

Gọi tam giác nội tiếp đường tròn ( C) có phương trình là

x² + y² + 2ax + 2by + c = 0 (a² + b² - c > 0 )

Do ba điểm A; B và C thuộc đường tròn là:

⇒ Bán kính đường tròn ( C) là R = 

Chọn C.

Ví dụ 6: Tâm của đường tròn qua ba điểm A( 2; 1); B( 2; 5) ; C( -2; 1) thuộc đường thẳng có phương trình

A. x - y + 3 = 0    B. x - y - 3 = 0    C. x + 2y - 3 = 0    D. x + y + 3 = 0

Hướng dẫn giải

Gọi phương trình ( C) có dạng: x² + y² - 2ax - 2by + c = 0 (a² + b² + c > 0 ) . Tâm I (a; b)

 ⇒ I(0; 3)

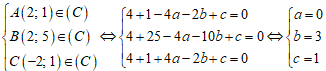
Lần lượt thế tọa độ I vào các phương trình để kiểm tra thì điểm I thuộc đường thẳng

x - y - 3 = 0

Chọn B.

Ví du 7: Cho tam giác ABC có A(2; 1); B( 3; 4) và C(-1; 2). Gọi I là tâm của đường tròn ngoại tiếp tam giác ABC. Tính OI?

A. 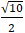    B. 2√2    C. √10    D. 

Lời giải

Ta có: AB→( 1; 3)và AC→(-3; 1 )

⇒ AB→. AC→ = 1.(-3) + 3.1 = 0

⇒ AB vuông góc AC nên tam giác ABC vuông tại A.

⇒ Tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC.

+ Tọa độ tâm I- trung điểm của BC là:

⇒ Khoảng cách OI = 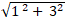 = √10

Chọn C.

Ví dụ 8: Tâm của đường tròn qua ba điểm A( 2; 1) ; B( 2; 5) và C( -2; 1) thuộc đường thẳng có phương trình

A. x - y + 3 = 0.    B. x + y - 3 = 0    C. x - y - 3 = 0    D. x + y + 3 = 0

Hướng dẫn giải

Phương trình đường tròn (C) có dạng:

x² + y² - 2ax – 2by + c = 0 ( a² + b² – c > 0)

 ⇒ I( 0; 3)

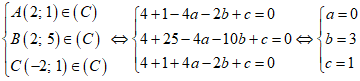
Vậy tâm đường tròn là I( 0; 3) .

Lần lượt thay tọa độ I vào các phương trình đường thẳng thì chỉ có đường thẳng

x - y + 3 = 0 thỏa mãn.

Chọn A.