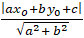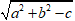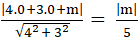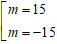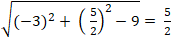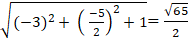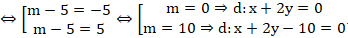Cách giải bài toán Đường tròn tiếp xúc với đường thẳng

A. Phương pháp giải

+ Cho đường tròn ( C) tâm I( a;b) bán kính R và đường thẳng d.

Đường thẳng d tiếp xúc với đường tròn ( C) khi và chỉ khi : d(I, d)= R

+ Trục tung có phương trình x= 0 nên để đường tròn tiếp xúc với trục tung khi và chỉ khi:

 = R hay R = |a|

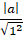
+ Trục hoành có phương trình y= 0 để đường tròn tiếp xúc với trục hoành khi và chỉ khi:

 = R hay R = |b|.

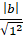
+ Đường tròn tiếp xúc với hai trục tọa độ khi và chỉ khi:

R = |a| = |b|.

Chú ý: Cho đường thẳng d: ax + by + c= 0 và điểm M(x0; y0) . Khoảng cách từ điểm M đến đường thẳng d là: d(M; d) = 

B. Ví dụ minh họa

Ví dụ 1: Cho phương trình x² + y² - 4x + 2my + m² = 0 (1). Mệnh đề nào sau đây sai?

A. Phương trình ( 1) là phương trình đường tròn, với mọi giá trị của m.

B. Đường tròn (1) luôn tiếp xúc với trục tung.

C. Đường tròn ( 1) tiếp xúc với các trục tọa độ khi và chỉ khi m = 2.

D. Đường tròn (1) có bán kính R = 2.

Hướng dẫn giải

+ Xét x² + y² - 4x + 2my + m² = 0 có a = 2; b = -m và c = m²

⇒ a² + b² - c = 4 + m² - m² = 4 > 0 với mọi m nên A và D đúng.

+ Vì a = R = 2 nên B đúng.

+ Từ đó suy ra C sai, vì đường tròn tiếp xúc với trục hoành Ox khi và chỉ khi

|b| = |m| = 2 ⇔ m = ±2

Chọn C .

Ví dụ 2: Đường tròn (C) tâm I( 4;3) và tiếp xúc với đườngthẳng ∆: 3x - 4y + 5 = 0 có phương trình là

A. (x - 4)² + (y - 3) 2 = 2.    B. (x - 4)² + (y - 3)² = 1.

C. (x - 4)² + (y - 3)² = 4.    D. (x - 4)² + (y - 3)² = 3

Lời giải

Do đường tròn ( C) tiếp xúc với đường thẳng ∆ nên khoảng cách từ tâm I đến đường thẳng ∆ bằng bán kính đường tròn .

⇒ (C) có bán kính R = d(I, ∆) = 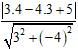 = 1.

Do đó, (C) có phương trình : (x - 4)² + (y - 3)² = 1.

Chọn B.

Ví dụ 3: Cho đường tròn (C): x² + y² - 2ax - 2by + c = 0 (a² + b² - c > 0) . Hỏi mệnh đề nào sau đây sai?

A. ( C) có bán kính R = 

B. ( C) tiếp xúc với trục hoành khi và chỉ khi b² = R².

C. ( C) tiếp xúc với trục tung khi và chỉ khi a = R.

D. ( C) tiếp xúc với trục tung khi và chỉ khi b² = c.

Hướng dẫn giải

Xét phương án C:

( C) tiếp xúc với trục tung Oy khi và chỉ khi: d(I, y'oy) = R ⇔ |a| = R.

Do đó đáp án sai vì nếu a = - 9 ⇒ R = -9 < 0 (vô lý)

Chọn C.

Ví dụ 4: Mệnh đề nào sau đây đúng?
Đường tròn (x + 2)² + (y - 3)² = 9 tiếp xúc với trục tung.
Đường tròn (x - 3)² + (y + 3)² = 9 tiếp xúc với các trục tọa độ.

A. Chỉ (I).    B. Chỉ (II).    C. Cả (I) và (II).    D. Không có.

Hướng dẫn giải

+ Xét đường tròn : (x + 2)² + ( y - 3)² = 9 có a = -2; b = 3 và R = 3

Vì |b| = 3 = R nên đường tròn tiếp xúc với trục hoành Ox nên ( I) sai.

+ Xét đường tròn: ( x - 3)² + (y + 3)² = 9 có a = 3; b = -3 và R = 3

Vì |a| = |b| = 3 = R nên đường tròn tiếp xúc với các trục tọa độ nên (II) đúng.

Chọn B.

Ví dụ 5: Với giá trị nào của m thì đường thẳng (d): 4x + 3y + m = 0 tiếp xúc với đường tròn x² + y² - 9 = 0 ?

A. m = ±15    B. m = ±√3    C. m = - 3    D. m = 3

Hướng dẫn giải

Đường tròn x² + y² - 9 = 0 có tâm I (0; 0) và bán kính R = 3.

Khoảng cách từ tâm I(0; 0) đến đường thẳng (d) là

d(I; d) = 

Để đường thẳng d tiếp xúc với đường tròn khi và chỉ khi: d(I;d)= R

⇔  = 3 ⇔ |m| = 15 nên m = ± 15

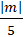
Chọn A.

Ví dụ 6: Đường tròn có tâm O và tiếp xúc với đường thẳng d : x + y - 4√2 = 0 . Hỏi bán kính của đường tròn bằng bao nhiêu?

A. 4√2    B. 4    C. 2    D. 8

Hướng dẫn giải

Khoảng cách từ tâm O(0; 0) đến đường thẳng (d) là

d(O; d) = 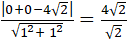 = 4

Để đường tròn tâm O tiếp xúc với đường thẳng d thì khoảng cách từ tâm O đến đường thẳng d bằng bán kính R.

⇒ Bán kính đường tròn ( C): R = 4.

Chọn B.

Ví dụ 7: Nếu đường tròn (C): (x - 1)² + (y - 3)² = R² tiếp xúc với đường thẳng d: 5x + 12y - 60 = 0 thì giá trị của R là:

A. 2√2    B. 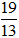    C. √5    D. √2

Hướng dẫn giải

Đường tròn (C): (x - 1)² + (y - 3)² = R² có tâm I (1; 3) bán kính R.

Đường thẳng d: 5x + 12y - 60 = 0 tiếp xúc với đường tròn (C) khi

R = d( I; d) =  =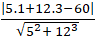 

Chọn B.

Ví du 8. Đường tròn (C) có tâm I( 2; 3) và tiếp xúc với đường thẳng
(d): 6x - 8y + 22 = 0 có phương trình là:

A. ( x + 2)² + (y - 3)² = 4    B. (x - 2)² + ( y - 3)² = 1

C. (x + 2)² + (y + 3)² = 9    D. Tất cả sai

Lời giải

Khoảng cách từ tâm I đến đường thẳng d là :

d(I; d) = 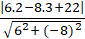 = 1

Mà đường tròn ( C) tiếp xúc với đường thẳng d nên R= 1

⇒ Phương trình đường tròn( C): (x - 2)² + (y - 3)² = 1

Chọn B.

Ví dụ 9 . Đường tròn x² + y² + 4y = 0 không tiếp xúc đường thẳng nào trong các đường thẳng dưới đây?

A. x - 2 = 0    B. x + y - 3 = 0    C. x + 2 = 0    D. Trục hoành.

Hướng dẫn giải

Đường tròn có tâm I( 0; -2) , bán kính R = 2.

– Khoảng cách từ tâm I đến đường thẳng (Δ₁) : x - 2 = 0

d(I, Δ₁) = 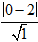 = 2 = R ⇒ (C) tiếp xúc (Δ₁)

– Tương tự: ( C) tiếp xúc (Δ₂): x + 2 = 0; ( C) tiếp xúc trục hoành Ox: y= 0

– Khoảng cách từ tâm I đến đường thẳng (Δ₃) :

d(I,Δ₃)= 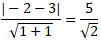 ≠ R

⇒ ( C ) không tiếp xúc (Δ₃)

Chọn B.

Ví dụ 10. Đường tròn (C) đi qua điểm M(2; -1) và tiếp xúc với hai trục tọa độ Ox; Oy có phương trình là:

A. (x + 1)² + (y - 1)² = 1 hoặc (x + 5)² + (y - 5)² = 25

B. (x - 1)² + (y + 1)² = 1

C. ( x - 5)² + (y + 5)² = 25

D. (x - 1)² + (y + 1)² = 1 hoặc ( x - 5)² + (y + 5)² = 25

Lời giải

Gọi tâm đường tròn là I = ( a; b)

Do đường tròn tiếp xúc với hai trục tọa độ nên R = d(I; Ox) = d(I; Oy)

⇔ R = |a| = |b|.

Vì đường tròn đi qua điểm M(2; -1) thuộc góc phần tư thứ tư (IV) nên a = - b và a > 0

⇒ I( a; -a)

Ta có: R = IM ⇔ R² = IM² ⇔ a² = ( a - 2)² + (-a + 1)²

⇔ a² = a² - 4a + 4 + a² - 2a + 1

⇔ a² - 6a + 5 = 0 ⇔ a = 1 hoặc a = 5

+ Với a = 1 thì tâm đường tròn là I (1; -1) và bán kính R = 1

⇒ Phương trình ( C): ( x - 1)² + ( y + 1)² = 1.

+ Với a = 5 thì tâm đường tròn là I (5; -5) và bán kính R = 5

⇒ Phương trình đường tròn là ( x - 5)² + (y + 5)² = 25

Chọn D.

Ví dụ 11 : Với những giá trị nào của m thì đường thẳng ∆ : 4x + 3y + m = 0 tiếp xúc với đường tròn ( C): x² + y² - 9 = 0.

A. m = -3    B. m = 3 và m = -3 .    C. m = 3    D. m = 15 và m = -15

Hướng dẫn giải

Đường tròn (C) có tâm I(0; 0) và bán kính R = 3.

Để ∆ tiếp xúc ( C) khi và chỉ khi :

d(I, Δ) = R ⇔ 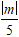 = 3 ⇔ 

Chọn D.

Ví dụ 12. Đường tròn nào sau đây tiếp xúc với trục Ox?

A. x² + y² - 2x - 10y = 0    B. x² + y² + 6x + 5y + 9 = 0

C. x² + y² - 10y + 1= 0    D. x² + y² - 5 = 0

Hướng dẫn giải

Đường tròn: x² + y² - 2ax - 2by + c = 0 tiếp xúc với trục Ox khi và chỉ khi khoảng cách từ tâm đường tròn I( a; b) đến trục Ox: y = 0 là bằng R.

⇔ |b|=R

+ Phương án A: là đường tròn có a = 1; b = 5 và c = 0 nên bán kính đường tròn là
R = 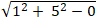 = √26

⇒ |b| ≠ R nên đường tròn này không tiếp xúc với trục Ox.

+ Phương án B là đường tròn có a = -3; b = 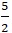 và c = 9

⇒ R = 

⇒ |b| = R nên đường tròn này tiếp xúc với trục Ox.

+ Tương tự các đường tròn ở phương án C và D không tiếp xúc với trục Ox

Chọn B.

Ví dụ 13. Đường tròn nào sau đây tiếp xúc với trục Oy?

A. x² + y² - 10y + 1= 0    B. x² + y² + 6x + 5y - 1 = 0

C. x² + y² - 2x = 0    D. x² + y² - 5 = 0

Hướng dẫn giải

Đường tròn: x² + y² - 2ax - 2by + c = 0 tiếp xúc với trục Oy khi và chỉ khi khoảng cách từ tâm đường tròn I( a; b) đến trục Oy: x= 0 là bằng R.

⇔ |a| = R.

+ Phương án A: Là đường tròn có a = 0; b = 5 và c = 1 nên bán kính

R = 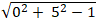 = √26

⇒|a| ≠ R nên đường tròn này không tiếp xúc với Oy.

+ Phương án B: là đường tròn có a = -3; b = - 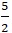 và c = - 1 nên

R = 

⇒ |a| ≠ R nên đường tròn này không tiếp xúc với Oy.

+ Phương án C: là đường tròn có a = 1; b = 0; c = 0 nên R = 1

⇒ |a| = R nên đường tròn này tiếp xúc với Oy.

Chọn C.

Ví dụ 14: Cho đường tròn (C); x² + y² + 2x – 6y + 5 = 0 . Phương trình tiếp tuyến của (C) song song với đường thẳng (a) : x + 2y - 15 = 0 là

A. x + 2y = 0 và x + 2y - 10 = 0    B. x + 2y = 2 và x + 2y + 8 = 0

C. x + 2y + 2 = 0 và x + 2y - 8 = 0    D. tất cả sai

Hướng dẫn giải

Đường tròn (C) có tâm I( -1;3) và bán kính R = 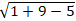 = √5.

Do tiếp tuyến d song song với đường thẳng a nên d có dạng: x + 2y - m = 0

d là tiếp tuyến của (C) khi và chỉ khi:

d(I, d) = R ⇔ 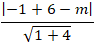 = √5 ⇔ |m-5|=5

Chọn A.

Ví dụ 15. Đường tròn ( C) có tâm I( -2; - 3) và tiếp xúc với đường thẳng
(d): 3x - 4y - 1 = 0 có phương trình là:

A. (x + 2)² + (y + 3)² = 1    B. (x - 2)² + (y - 3)² = 4

C. (x - 2)² + (y - 3)² = 9    D. ( x + 2)² + ( y + 3)² = 4

Lời giải

Khoảng cách từ tâm I đến đường thẳng d là :

d(I; d) = 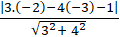 = 1

Mà đường tròn ( C) tiếp xúc với đường thẳng d nên R = 1

⇒ Phương trình đường tròn( C):

(x + 2)² + (y + 3)² = 1

Chọn A.

Ví dụ 16. Đường tròn (C) tâm I( -4; 3) và tiếp xúc với trục tung có phương trình là

A. x² + y² - 4x + 3y + 1 = 0.    B. (x + 4)² + (y - 3)² = 16.

C. (x - 4)² + (y + 3)² = 9.    D. x² + y² + 8x - 6y + 1 = 0.

Lời giải

Do đường tròn (C) tiếp xúc với trục tung Oy và có tâm I( -4; 3) nên:

a = - 4; b = 3 và R = |a| =4.

Do đó, (C) có phương trình: (x + 4)² + (y - 3)² = 16.

Chọn B.