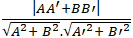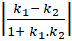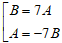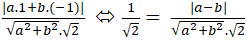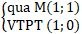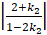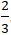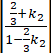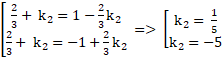Viết phương trình đường thẳng d đi qua M và tạo với d’ một góc
Viết phương trình đường thẳng d đi qua M và tạo với d’ một góc Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Viết phương trình đường thẳng d đi qua M và tạo với d’ một góc
Viết phương trình đường thẳng d đi qua M và tạo với d’ một góc
A. Phương pháp giải
Cho đường thẳng ∆ và điểm M(a; b). Viết phương trình đường thẳng d đi qua M và tạo với đường thẳng ∆ một góc α.
+ Cách 1:
- Gọi n→(A; B) là VTPT của đường thẳng d.
Tìm VTPT n'→( A’; B’) của đường thẳng ∆.
- Do góc giữa đường thẳng d và ∆ bằng α nên:
Cosα =
Giải phương trình trên ta được A = k.B. Chọn A =.... ⇒ B..
⇒ VTPT của đường thẳng d
⇒ Phương trình đường thẳng d.
+ Cách 2:
- Đường thẳng ∆ có hệ số góc k1.
- Giả sử đường thẳng d có hệ số góc k2.
- Do góc giữa hai đường thẳng d và ∆ là α nên :
Tanα =
Phương trình trên là phương trình ẩn k2. Giải hệ phương trình ta được k2
⇒ Phương trình đường thẳng d.

B. Ví dụ minh họa
Ví dụ 1 : Cho đường thẳng d : 3x - 4y - 12 = 0. Phương trình các đường thẳng qua
M(2 ; -1) và tạo với d một góc 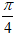
A. 7x - y - 15 = 0 ; x + 7y + 5 = 0 B. 7x + y - 15 = 0 ; x - 7y + 5 = 0
C. 7x - y + 15 = 0 ; x + 7y - 5 = 0 D. 7x + y + 15 = 0 ; x - 7y - 5 = 0
Lời giải
Gọi n→( A , B) và A2 + B2 > 0 là véc tơ pháp tuyến của ∆
Đường thẳng d có VTPT n'→( 3 ; -4)
Ta có:
⇔ 7A2 + 48AB - 7B2 = 0 ⇔
+ Với B = 7A chọn A = 1 ; B = 7 ⇒ (d) : qua M(2 ; -1) và VTPT (1 ; 7)
⇒ Phương trình (d) : 1( x - 2) + 7( y + 1) = 0 hay x + 7y + 5 = 0
+ Với A = - 7B chọn A = 7 ; B = - 1 ⇒ (d) đi qua M( 2 ; -1) và VTPT ( 7 ; -1)
⇒ Phương trình (d) : 7( x - 2) – 1( y + 1) = 0 hay 7x - y - 15 = 0
Vậy có hai đường thẳng thỏa mãn là : x + 7y + 5 = 0 và 7x - y - 15 = 0.
Chọn A.
Ví dụ 2. Viết phương trình đường thẳng (d) qua M( -1; 2) và tạo với trục Ox một góc 600.
A. √3x - y + √3 + 2 = 0 B. √3x - y - √3 + 2 = 0
C. √3x - y + 2 = 0 D. √3x + y - √3 + 2 = 0
Lời giải
Do (d) tạo với trục Ox một góc 600 nên có hệ số góc k = tan 600 = √3.
Phương trình d là: y = √3(x + 1) + 2 ⇔ √3x - y + √3 + 2 = 0 .
Chọn A.
Ví dụ 3. Biết rằng có đúng hai giá trị của tham số k để đường thẳng d: y = kx tạo với đường thẳng ∆: y = x một góc 600. Tổng hai giá trị của k bằng:
A. - 8 B. - 4 C. - 1 D. 1
Lời giải
Ta có đường thẳng d : y = kx ⇔ kx - y = 0 nên d nhận VTPT nd→( k; -1)
Đường thẳng ∆ : y = x hay x - y = 0 nên ∆ nhận VTPT n∆→( 1; -1)
Để hai đường thẳng này tạo với nhau góc 600 thì:
( nd→; n∆→) = 600 ⇒ cos(nd→; n∆→)= cos 600
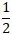
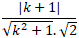
Phương trình trên có hai nghiệm phân biệt theo hệ thức Vi- et ta có: k1 + k2 = - 4
Chọn B.
Ví dụ 4: Viết phương trình đường thẳng ∆ đi qua M(1;1) và tạo một góc 450 với đường thẳng d: x - y + 90 = 0
A. x - 1 = 0 B. y - 1 = 0 C. x + y - 2 = 0 D. Cả A và B đúng
Lời giải
+ Đường thẳng d có VTPT n→(1; -1) .
+ Gọi VTPT của ∆ là n'→(a; b) .
+ Do góc giữa hai đường thẳng d và ∆ là 450 nên:
cos450 =
⇔ 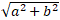
⇔ - 2ab = 0 ⇔ a = 0 hoặc b = 0
+ Nếu a = 0; chọn b = 1.
Đường thẳng ∆:
⇒ Phương trình ∆: 0(x - 1) + 1( y - 1) = 0 hay y - 1 = 0
+ Nếu b = 0; chọn a = 1.
Đường thẳng ∆:
⇒ Phương trình ∆: 1(x - 1) + 0( y - 1) = 0 hay x - 1 = 0
Chọn D.
Ví dụ 5: Viết phương trình đường thẳng ∆ qua điểm M(5; 1) và tạo thành một góc 450 với đường thẳng d: y = -2x + 4
A. y = 3x - 10 B. y = 3x - 14 C. y = 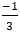
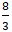
Lời giải
Hệ số góc của đường thẳng d là k1 = -2.
Gọi hệ số góc của đường thẳng ∆ là k2.
Do góc giữa hai đường thẳng là 450 nên :
Tan450 = 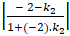
⇔
+ Với k2 = 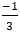
y= 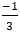
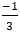
+ Với k2 = 3 đường thẳng ∆ qua M(5; 1) và hệ số góc k2 nên có phương trình :
y = 3( x - 5) + 1 hay y = 3x - 14
chọn D.
Ví dụ 6: Viết phương trình đường thẳng ∆ qua điểm M(2; 1) và tạo thành một góc 450 với đường thẳng d: 2x + 3y + 4 = 0
A. y = -5x - 10 B. y = -5x + 11 C. y = 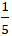
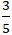
Lời giải
Hệ số góc của đường thẳng d là k1= -
Gọi hệ số góc của đường thẳng ∆ là k2.
Do góc giữa hai đường thẳng là 450 nên :
Tan450 = 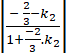
⇔
+ Với k2 = 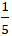
y = 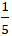
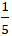
+ Với k2 = -5 đường thẳng ∆ qua M(2; 1) và hệ số góc k2 nên có phương trình :
y = - 5( x - 2) + 1 hay y = -5x + 11
Chọn D.