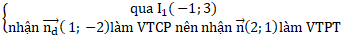A. Phương pháp giải

Cho đường tròn (C₁): tâm I₁( x₁; y₁); bán kính R₁.

Đường tròn (C₂): tâm I₂(x₂; y₂); bán kính R₂.

+ Để hai đường tròn này đối xứng với nhau qua điểm M thì M là trung điểm của I₁I₂ và R₁ = R₂.

* Nếu cho trước đường tròn ( C₁) có tâm I₁ bán kính R và điểm M. Để viết được phương tròn ( C₂ ) đối xứng với đường tròn (C₁) qua M ta cần làm như sau:

- Bước 1: Tìm điểm I₂ đối xứng với I₁ qua M ( khi đó M là trung điểm I₁I₂).

- Bước 2: Đường tròn ( C₂) tâm I₂ và bán kính là R.

⇒ Phương trình đường tròn (C₂).

* Cho đường tròn (C₁) tâm I₁ bán kính R và đường thẳng d. Để viết được đường tròn (C₂) đối xứng với đường tròn (C₁) qua d ta cần:

- Bước 1: Xác định điểm I₂ đối xứng điểm I₁ qua d.

- Bước 2: Lập phương trình đường tròn ( C₂) tâm I₂ và bán kính R

B. Ví dụ minh họa

• Ví dụ 1: Cho đường tròn (C₁): x² + y² - 4x - 6y - 2 = 0 và đường thẳng d: 3x - 4y - 9 = 0. Phép đối xứng qua đường thẳng d biến đường tròn ( C₁) thành đường tròn ( C₂). Tính I₁I₂ trong đó I₁; I₂ lần lượt là tâm của hai đường tròn ( C₁); (C₂)?

  A. 5    B. 6    C. 3    D. 10

  Lời giải

  + Đường tròn ( C₁) có tâm I₁(2;3).

  + Khoảng cách từ I₁ đến đường thẳng d:

  d(I₁; d) =  = 3

  + Do hai đường tròn đối xứng với nhau qua đường thẳng d nên d là đường trung trực của I₁I₂. Gọi H là giao điểm của I₁I₂ với đường thẳng d

  ⇒ d(I₁;d) = I₁H = I₂H = 3

  ⇒ I₁I₂ = I₁H + HI₂ = 3 + 3 = 6

  Chọn B

Ví dụ 2: Viết phương trình đường tròn (C₂) đối xứngvới đường tròn
(C₁): x² + y² - 2x = 0. Qua điểm A( 2; -1) ?

A. (x + 3)² + (y - 2)² = 1    B. (x - 3)² + (y - 2)² = 1

C. (x - 3)² + (y + 2)² = 1    D. (x + 3)² + (y + 2)² = 1

Lời giải

+ Đường tròn ( C₁) có tâm I₁ (1; 0) và bán kính R₁ = 1.

+ Do đường tròn (C₂) đối xứng với đường tròn (C₁) qua điểm A nên hai tâm của hai đường tròn đối xứng với nhau qua điểm A đồng thời R₁ = R₂ = 1.

+ Gọi I₂ là tâm của đường tròn ( C₂) thì tọa độ điểm I₂:

 ⇒ I₂( 3; -2)

⇒ Phương trình đường tròn ( C₂): (x - 3)² + (y + 2)² = 1

Chọn C.

Ví dụ 3: Cho đường tròn ( C₁): x² + y² - 8x - 4y - 5 = 0 và điểm M. Qua phép đối xứng tâm M biến đường tròn ( C₁) thành đường tròn ( C₂) có bán kính R₂ . Tính R₂?

A. 1    B. 3    C. 5    D. 10

Lời giải

Đường tròn ( C₁) có tâm I₁( 4; 2) và bán kính R₁ =  = 5

Qua đối xứng tâm M biến đường tròn ( C₁) thành đường tròn (C₂)

⇒ Hai đường tròn này có cùng bán kính và hai tâm đối xứng với nhau qua điểm M

⇒ bán kính R₂ = R₁ = 5.

Chọn C.

Ví dụ 4: Cho đường tròn ( C₁): x² + y² + 2x - 4y - 1 = 0 và đường tròn
( C₂): x² + y² - 2x + 6y - 2 = 0. Tìm tâm phép đối xứng biến ( C₁) thành ( C₂)?

A. ( 1; - 2)    B. ( 2; 3)    C. Không tồn tại    D. Tất cả sai

Lời giải

+ Đường tròn ( C₁) có tâm I₁ (-1; 2) và bán kính R₁ = √6.

+ Đường tròn (C₂) có tâm I₂(1; -3) và bán kính R₂ = √12

⇒ R₁ ≠ R₂.

⇒ Không có phép đối xứng tâm biến đường tròn này thành đường tròn kia.

Chọn C.

Ví dụ 5: Cho đường tròn ( C₁): x² + y² + 2x - 6y - 4 = 0 và đường thẳng d: x - 2y - 3 = 0. Viết phương trình đường tròn ( C₂) đối xứng với đường tròn ( C₁) qua d?

A. (x + 3)² + (y - 3)² = 14    B. (x - 2)² + (y - 5)² = 14

C. (x - 1)² + (y + 4)² = 14    D. (x - 3)² + (y + 5)² = 14

Lời giải

+ Đường tròn (C₁) có tâm I₁( - 1; 3) và bán kính R₁ = √14

+ Giả sử đường tròn ( C₂) có tâm I₂ và bán kính R₂.

+ Do hai đường tròn ( C₁) và (C₂) đối xứng với nhau qua đường thẳng d nên:

R₂ = R₁ = √14 và hai tâm I₁, I₂ đối xứng nhau qua đường thẳng d.

+ Ta tìm điểm I₂.

- Đường thẳng I₁I₂: 

⇒ Phương trình I₁I₂: 2(x + 1) + 1(y - 3) = 0 hay 2x + y - 1 = 0.

- Gọi giao điểm của d và I₁I₂ là H ⇒ H( 1; - 1).

Khi đó; H là trung điểm của I₁I₂ nên tọa độ điểm I₂:

 ⇒ I₂( 3; -5)

⇒ Phương trình đường tròn ( C₂): (x - 3)² + (y + 5)² = 14

Chọn D.

Ví dụ 6: Cho đường tròn (C₁): x² + y² + 8x - 10y - 10 = 0 và đường thẳng d: 5x + 4y = 0. Viết phương trình đường tròn (C₂) đối xứng với đường tròn ( C₁) qua đường thẳng d?

A. x² + y² + 10x - 10y - 10 = 0    B. x² + y² + 20x - 10y - 10 = 0

C. x² + y² - 10x - 20y - 15 = 0    D. x² + y² + 20x + 10y - 15 = 0

Lời giải

+ Đường tròn (C₁): tâm I₁( -4; 5).

Ta thấy điểm I₁ thuộc đường thẳng d nên phép đối xứng qua đường thẳng d biến đường tròn (C₁) thành chính nó.

⇒ (C₂) ≡ (C₁): x² + y² + 8x - 10y - 10 = 0.

Chọn A.

Ví dụ 7: Cho đường tròn ( C₁): x² + y² - 10x - 20y - 15 = 0 và điểm A(5; 10). Viết phương trình đường tròn (C₂) đối xứng với đường tròn (C₁) qua điểm A?

A. x² + y² - 10x + 20y - 15 = 0    B. x² + y² + 10x - 20y - 15 = 0

C. x² + y² - 10x - 20y - 15 = 0    D. Tất cả sai

Lời giải

+ Đường tròn ( C₁) có tâm I₁(5;10)

⇒ Điểm I₁ ≡ A.

⇒ Qua đối xứng tâm A biến điểm I₁ thành chính nó nên biến đường tròn C₁ thành chính nó.

⇒ (C₂) ≡ (C₁): x² + y² - 10x - 20y - 15 = 0.

Chọn C

Ví dụ 8: Cho hai đường tròn ( C₁): tâm I₁(1; -2) bán kính R₁ = 2 và đường tròn (C₂):
Tâm I₂( 3; 2) bán kính R₂ = 2. Tìm tâm phép đối xứng của đường tròn (C₁) và ( C₂)?

A. M(2; 0)    B. M(4; 0)    C. M( 2; 4)    D. M (-2; -4)

Lời giải

Do hai đường tròn đã cho có R₁ = R₂ nên tồn tại điểm M để qua điểm M biến đường tròn này thành đường tròn kia.

Khi đó, M là trung điểm của I₁I₂. Suy ra tọa độ điểm M là:

 ⇒ M( 2 ; 0)

Vậy qua điểm M (2; 0) biến đường tròn này thành đường tròn kia.

Chọn A.

C. Bài tập vận dụng

• Câu 1: Cho đường tròn ( C₁): x² + y² + 12x - 8y - 1 = 0 và điểm A(-6; 4). Viết phương trình đường tròn (C₂) đối xứng với đường tròn (C₁) qua điểm A?

  A. x² + y² + 14x + 8y - 1 = 0    B. x² + y² - 12x + 8y - 1 = 0

  C. x² + y² + 12x - 8y - 1 = 0    D. Tất cả sai

Câu 2: Viết phương trình đường tròn (C₂) đối xứngvới đường tròn (C₁): x² + y² + 4y = 0 Qua điểm A(0; 4) ?

A. (x + 3)² + (y - 2)² = 4    B. (x - 3)² + (y - 2)² = 4

C. x² + (y - 10)² = 4    D. (x + 3)² + y² = 4

Câu 3: Cho đường tròn ( C₁): x² + y² - 2x + 8y - 8 = 0 và điểm M. Qua phép đối xứng tâm M biến đường tròn ( C₁) thành đường tròn ( C₂) có bán kính R₂. Tính R₂?

A. 1    B. 3    C. 5    D. 10

Câu 4: Cho đường tròn (C₁): x² + y² + 8y - 2 = 0 và đường tròn
(C₂): x² + y² + 2x - 4y - 1 = 0. Tìm tâm phép đối xứng biến ( C₁) thành ( C₂)?

A. ( 1;-2)    B. ( 2; 3)    C. Không tồn tại    D. Tất cả sai

Câu 5: Cho đường tròn ( C₁): x² + y² + 4x - 4y - 1 = 0 và đường thẳng d: 2x - y - 3 = 0. Viết phương trình đường tròn ( C₂) đối xứng với đường tròn ( C₁) qua d?

A. (x + 3)² + (y - 3)² = 9    B. (x - 2)² + (y - 5)² = 9

C. (x -  )² + (y +  )² = 9    D. ( x -  )² + (y +  )² = 9

Câu 6: Cho hai đường tròn ( C₁): tâm I₁(3; 8) bán kính R₁ = 6 và đường tròn (C₂): Tâm I₂( -7; 4) bán kính R₂ = 6. Tìm tâm phép đối xứng của đường tròn (C₁) và ( C₂)?

A. M(2; 0)    B. M(4; 0)    C. M( -2; 6)    D. M (-2; -4)

Câu 7: Cho đường tròn (C₁): x² + y² + 4x - 4 = 0 và đường thẳng d: x + y + 2 = 0. Viết phương trình đường tròn (C₂) đối xứng với đường tròn ( C₁) qua đường thẳng d?

A. x² + y² + 4y - 4 = 0    B. x² + y² + 2x - 2y - 6 = 0

C. x² + y² + 4x - 4 = 0    D. x² + y² + 20x + 10y - 15 = 0

Câu 8: Cho đường tròn (C₁): x² + y² – 6x + 2y - 1 = 0 và đường thẳng
d: 3x + 4y + 10 = 0. Phép đối xứng qua đường thẳng d biến đường tròn ( C₁) thành đường tròn ( C₂). Tính I₁I₂ trong đó I₁; I₂ lần lượt là tâm của hai đường tròn ( C₁); (C₂)?

A. 5    B. 6    C. 3    D. 10