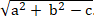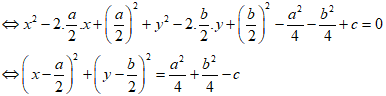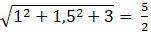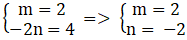Cách nhận dạng, xác định phương trình đường tròn: tìm tâm, bán kính

A. Phương pháp giải

+ Phương trình x² + y² - 2ax - 2by + c = 0 là phương trình đường tròn nếu:

a² + b² - c > 0. Khi đó; phương trình trên là phương trình đường tròn tâm I(a;b) và bán kính R = 

+ Phương trình (x - a)² + (y - b)² = R² là đường tròn tâm I(a; b) và bán kính R.

B. Ví dụ minh họa

Ví dụ 1. Cho đường tròn (C) : x²+ y² + 8x + 6y + 9 = 0. Mệnh đề nào sau đây sai?

A. (C) không đi qua điểm O.    B. tâm I( -4 ; -3).

C. bán kính R = 4.    D. (C) đi qua điểm M(-1 ; 0) .

Lời giải

+Ta có a = -4; b = -3 ; c = 9 và a² + b² - c = 16 + 9 - 9 = 16 > 0

Suy ra (C) là đường tròn tâm I( -4; -3) và R = 4

Vậy B; C đúng.

+ Thay O vào (C) ta có: 0² + 0² + 8.0 + 6.0 + 9 = 0 vô lí . Vậy A đúng.

+ Thay M( -1; 0) vào (C) ta có: (-1)² + 0² + 8.(-1) + 6.0 + 9 = 0 ( vô lý). Vậy D sai.

Chọn D.

Ví dụ 2. Để x²+ y²- ax - by + c = 0 là phương trình đường tròn, điều kiện cần và đủ là

A. 2a² + 2b² - c > 0.    B. a² + b² - 2c > 0.    C. a² + b² - 4c > 0.    D. a² + b² + c > 0.

Lời giải

Ta có:

x² + y² - ax - by + c = 0 (1)

Vậy điều kiện để (1) là phương trình đường tròn:

 - c > 0 hay a² + b² - 4c > 0

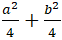
Chọn C.

Ví dụ 3. Phương trình nào sau đây là phương trình của đường tròn?
(I) x² + y² – 4x + 15y - 12 = 0.
(II) x² + y² – 3x + 4y + 20 = 0.
(III) 2x² + 2y² - 4x + 6y + 1 = 0 .

A. Chỉ (I).    B. Chỉ (II).    C. Chỉ (III).    D. Chỉ (I) và (III).

Lời giải

Ta xét các phương án:

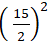
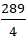
(I) có: a² + b² - c = 4 +  + 12 =  > 0

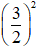
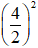
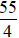
(II) có: a² + b² - c =  +  - 20 = -  < 0

(III) tương đương : x²+ y² – 2x - 3y + 0,5 = 0.

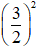
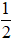
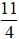
phương trình này có: a² + b² - c = 1 +  -  =  > 0

Vậy chỉ (I) và (III) là phương trình đường tròn.

Chọn D.

Ví dụ 4. Mệnh đề nào sau đây đúng? (1) Đường tròn (C₁) : x²+ y² – 2x + 4y - 4 = 0 có tâm I( 1; -2) bán kính R = 3. (2) Đường tròn (C₂) x²+ y² – 5x + 3y – 0,5 = 0 có tâm
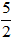
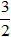
I(  ; -  ) bán kính R = 3.

A. Chỉ (1).    B. Chỉ (2).    C. cả hai    D. Không có.

Lời giải

Ta có: đường tròn (C₁) : a = 1, b = -2 ⇒ I(1; -2); R = 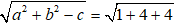 = 3

Vậy (1) đúng

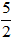
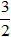
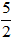
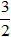
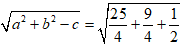
Đường tròn ( C₂): a =  , b = -  ⇒ I(  ; -  ); R =  = 3

Vậy (2) đúng.

Chọn C.

Ví dụ 5. Đường tròn 3x² + 3y² - 6x + 9y – 9 = 0 có bán kính bằng bao nhiêu ?

A. 2,5    B. 3    C. 2    D. 4

Lời giải

Ta viết lại phương trình đường tròn: x² + y² - 2x + 3y - 3 = 0

Suy ra a = 1; b = -1,5 và c = -3 và bán kính R = 

Chọn A.

Ví dụ 6. Cho đường tròn (C) : x² + y² - 4x + 3 = 0 . Hỏi mệnh đề nào sau đây sai?

A. tâm I( 2; 0)    B. bán kính R = 1

C. (C) cắt trục 0x tại 2 điểm.    D. (C) cắt trục Oy tại 2 điểm.

Lời giải

Cho x= 0 ta được : y² + 3 = 0 phương trình vô nghiệm.

Vậy (C) không có điểm chung nào với trục tung.

Chọn D.

Ví dụ 7. Cho phương trình x² + y² - 2mx - 4(m - 2)y + 6 - m = 0 (1). Tìm điều kiện của m để (1) là phương trình đường tròn.

A. đúng mọi m    B. m ∈( -∞; 1) ∪ ( 2; +∞)

C. m ∈ ( -∞; 1] ∪ [2; +∞)    D. Đáp án khác

Lời giải

Ta có: x² + y² - 2mx - 4(m - 2)y + 6 - m = 0 có:

a = m; b = 2m - 4; c = 6 - m

Để phương trình trên là phương trình đường tròn ⇔ a² + b² - c > 0.

⇔ m² + ( 2m - 4)² - (6 - m) > 0

⇔ m² + 4m² – 16m + 16 – 6 + m > 0

⇔ 5m² - 15m + 10 > 0 ⇔ m ∈ ( -∞; 1) ∪ ( 2; +∞)

Chọn B.

Ví dụ 8. Đường tròn x² + y² - 10x - 11 = 0 có bán kính bằng bao nhiêu?

A. 6    B. 2    C. 4    D. √6

Lời giải

Ta có hệ số a = 5; b = 0 và c = -11 nên bán kính là R = 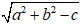 = 6

Chọn A.

Ví dụ 9: Cho phương trình: x² + y² - 2mx + 4y + 4 = 0. Tìm điều kiện của m để phương trình trên là phương trình đường tròn?

A. m > 1    B. m > 0    C. m ≠ 0    D. m > -1 hoặc m < 2

Lời giải

Phương trình x²+ y² - 2mx + 4y + 4 = 0 có a = m; b = -2 và c = 4.

Để phương trình đã cho là phương trình đường tròn nếu:

a² + b² - c > 0 hay m² + (-2)² - 4 > 0

⇔ m² > 0 ⇔ m ≠ 0

Chọn C.

Ví dụ 10: Cho phương trình x² + y² - 2mx + 4ny - 4 = 0. Tìm m và n để phương trình trên là phương trình đường tròn tâm I(2; 4)?

A. m = 1; n = -2    B. m = 2; n = -2    C. m = 4; n = -4    D. m = -2; n = 2

Lời giải

Phương trình x² + y² - 2mx + 4ny - 4 = 0 có:

a = m; b = -2n và c = -4

Ta có: a²+ b² - c = m² + 4n² + 4 > 0 với mọi m và n.

⇒ Phương trình trên luôn là phương trình đường tròn tâm I(m; -2n).

Để phương trình là phương trình đường tròn tâm I(2; 4) khi và chỉ khi:

Chọn B.

Ví dụ 11. Cho phương trình x² + y² + 2x – my + 1 = 0. Tìm m để phương trình đã cho là phương trình đường tròn có bán kính R = 2?

A. m = ± 8    B. m = 6    C. m = 10    D. m = ± 4

Lời giải

Phương trình x² + y² + 2x - my + 1 = 0 có:

a = -1; b = 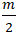 và c = 1

Để phương trình trên là phương trình đường tròn nếu: a²+ b²- c > 0

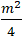
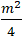
⇔ 1 +  - 1 > 0 ⇔  > 0 ⇔ m ≠ 0.

Với điều kiện m ≠ 0 thì phương trình trên là phương trình đường tròn có bán kính là:

R = 

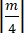
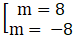
Theo đề bài ta có: R = 2 nên  = 2

⇔  ( thỏa mãn điều kiện )

Chọn A.

Ví dụ 12. Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?

A. 4x² + y² – 10x - 6y - 22 = 0    B. x² + y² - 2x - 8y + 20 = 0

C. x² + 2y² - 4y - 8y + 1 = 0    D. x² + y² - 4x + 6y - 12 = 0

Lời giải

Xét phương trình dạng : x² + y² - 2ax - 2by + c = 0 lần lượt tính các hệ số a ; b ; c. Để phương trình trên là phương trình đường tròn điều kiện là a² + b² - c > 0 .

+ Xét phương án D : có a = 2 ;b = 3 và c = -12

⇒ a² + b² - c = 4 + 9 + 12 = 25 > 0

⇒ Phương trình x² + y² - 4x + 6y - 12 = 0 là phương trình đường tròn.

+ Các phương trình 4x² + y² - 10x - 6y - 2 = 0 và x² + 2y²- 4x - 8y + 1 = 0 không có dạng đã nêu loại các đáp án A và C.

+ Phương án x² + y² - 2x - 8y + 20 = 0 không thỏa mãn điều kiện a² + b² - c > 0.

Chọn D.

Ví dụ 13. Cho phương trình x² + y² + 2mx + 2(m-1)y + 2m² = 0 (1) . Tìm điều kiện của m để (1) là phương trình đường tròn.

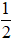
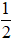
A. m <     B. m ≤     C. m > 1    D. m = 1

Lời giải

Ta có: trình x² + y² + 2mx + 2(m-1)y + 2m² = 0

⇒ a = -m; b = 1 - m; c = 2m²

Để phương trình trên là phương trình đường tròn thì:

a² + b² - c > 0 ⇔ m² + ( 1 - m)² - 2m² > 0

⇔ m² + 1 - 2m + m² - 2m² > 0

⇔ 1 - 2m > 0 ⇔ m < 

Chọn A.

Ví dụ 14. Cho phương trình x² + y² - 2ax - 2by + c = 0 (1) . Điều kiện để (1) là phương trình của đường tròn là

A. a² + b² - 4c > 0.    B. a²+ b² - c > 0.    C. a²+ b² - c² > 0.    D. a²+ b² - 2c > 0.

Lời giải

Ta có: x² + y² - 2ax - 2by + c = 0

Tương đương: (x - a)² + (y - b)² = a² + b² - c

Vậy điều kiện để (1) là phương trình đường tròn: a² + b² - c > 0.

Chọn B.