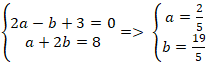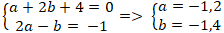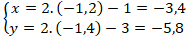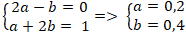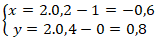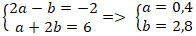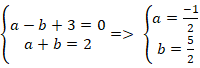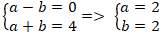A. Phương pháp giải

Bài toán: Cho đường thẳng d: ax + by + c = 0 và điểm A. Tìm điểm H là hình chiếu của A trên đường thẳng d:

+ Bước 1: Gọi tọa độ điểm H(x_H; y_H).

Vì điểm H thuộc d nên : ax_H + by_H + c = 0 (1).

+ Bước 2:Do AH vuông góc d nên AH→ là VTPT của d.

⇒ AH→(x_H - x_A; y_H - y_A) và n→(a; b) cùng phương

⇒ b(x_H - x_A) - a(y_H - y_A )= 0 (2)

+ Bước 3: giải hệ(1) và (2) ta được tọa độ điểm H.

B. Ví dụ minh họa

Ví dụ 1. Cho tam giác OBC có O(0; 0) ; B( 0; 6) và C(-6; 0). Gọi G là trọng tâm tam giác OBC. Tìm điểm G’ đối xứng với G qua BC?

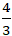
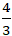
A. G’( -  ;-  )    B. G’( -1; 1)    C. G’(-2; 2)    D. G’(-4; 4)

Lời giải

+ ta có: OB→(0; 6); OC→( -6; 0)

⇒ OB= 6; OC= 6 và OB→.OC→ = 0.(-6) + 6.0 = 0

⇒ OB vuông góc OC và OB = OC

⇒ Tam giác OBC vuông góc tại O.

+ Do G là trọng tâm tam giác OBC nên tọa độ điểm G:

 ⇒ G( -2; 2)

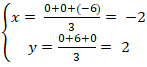
+ Gọi M là trung điểm của BC. Do tam giác OBC là vuông cân tại O nên đường trung tuyến OM đồng thời là đường cao nên OM vuông góc BC tại M.

⇒ G’ đối xứng với G qua BC nên M là trung điểm của GG’.

- M là trung điểm BC nên tọa độ điểm M: 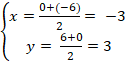 ⇒ M( - 3; 3)

- M là trung điểm GG’nên tọa độ điểm G’ là:

 ⇒ G’ ( -4; 4)

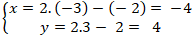
⇒ Vậy tọa độ điểm G’( - 4; 4)

Chọn D.

Ví dụ 2: Cho đường thẳng d: 2x - y + 3 = 0 và điểm M(0; 4). Tìm hình chiếu của M trên d?

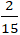
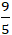
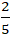
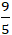
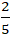
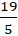
A. H(-  ;  ).    B. H( ;  ).    C. H( ;  ).    D. (4; -1)

Lời giải

+ Gọi H(a; b) là hình chiếu của M trên d.

+ Do H thuộc d nên 2a - b + 3 = 0 (1)

+ Ta có: MH→(a; b - 4).

Đường thẳng MH vuông góc d nên MH→ cùng phương n_d→(2; -1)

⇒  ⇔ -a = 2b - 8 hay a + 2b = 8 (2)

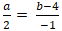
+ Từ (1) và (2) ta có hệ : 

⇒ Tọa độ điểm H( ;  )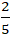

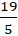
Chọn C.

Ví dụ 3: Cho đường thẳng d: x + 2y + 4 = 0 và điểm M(1; 3). Gọi M’(x; y) là điểm đối xứng với M qua d. Tính 2x - y?

A. 1    B. 2    C. 0    D. -1

Lời giải

+ Gọi H(a; b) là hình chiếu của M trên d.

+ Do H thuộc d nên a + 2b + 4 = 0 (1)

+ Ta có: MH→(a - 1; b - 3).

Đường thẳng MH vuông góc d nên MH→ cùng phương n_d→(1 ; 2)

⇒  ⇔ 2a - 2 = b - 3 hay 2a - b = -1 (2)

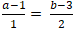
+ Từ (1) và (2) ta có hệ : 

⇒ Tọa độ điểm H(-1,2; -1,4).

+ Gọi M’đối xứng với M qua d thì H là trung điểm MM’ nên tọa độ điểm M’:

Vậy M’(-3,4; - 5,8) ⇒ 2x - y = -1

Chọn D.

Ví dụ 4: Cho đường thẳng d: 2x - y = 0 và điểm M(1 ;0). Gọi M’ (x; y) là điểm đối xứng với M qua d. Tính 4x + 3y?

A. 1    B. 2    C. 0    D. -1

Lời giải

+ Gọi H(a; b) là hình chiếu của M trên d.

+ Do H thuộc d nên 2a - b = 0 (1)

+ Ta có: MH→(a-1; b).

Đường thẳng MH vuông góc d nên MH→ cùng phương n_d→(2; -1)

⇒  ⇔ -a + 1 = 2b hay a + 2b = 1 (2)

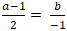
+ Từ (1) và (2) ta có hệ : 

⇒ Tọa độ điểm H(0,2; 0,4).

+ Gọi M’đối xứng với M qua d thì H là trung điểm MM’ nên tọa độ điểm M’:

Vậy M’(-0,6; 0,8) ⇒ 4x + 3y = 0

Chọn C.

Ví dụ 5: Cho đường thẳng d: 2x - 3y + 5 = 0 và điểm A(-1; 1). Tìm hình chiếu của điểm A trên d?

A. (2; -1)    B. (-2; -1)    C. (-1; 1)    D. (-1; 3)

Lời giải

Thay tọa độ điểm A vào phương trình đường thẳng d ta được :

2.(-1) - 3.1 + 5 = 0

⇒ Điểm A thuộc đường thẳng d nên hình chiếu của điểm A trên đường thẳng d là chính nó.

Chọn C.

Ví dụ 6: Cho đường thẳng (d): x + y - 3 = 0 và điểm M(2; 1) thuộc (d). Tập hợp những điểm A( x; y) sao cho M là hình chiếu của A trên d là đường thẳng nào?

A. x + y - 4 = 0    B. x + y - 1 = 0    C. x - y - 1 = 0    D. x - y + 3 = 0

Lời giải

+ Đường thẳng (d) có VTPT n→( 1; 1).

+ Vecto MA→( x - 2; y - 1).

Do M là hình chiếu của A trên d nên MA vuông góc d

⇒ Hai vecto MA→ và n_d→ cùng phương

⇔  ⇔ x - 2 = y - 1 hay x - y - 1 = 0

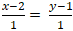
Vậy tập hợp những điểm A sao cho M là hình chiếu của A trên d là đường thẳng:
∆: x - y - 1 = 0

Chọn C.

Ví dụ 7: Cho đường thẳng d: 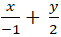 = 1 và điểm M(0; 3). Tìm hình chiếu của M trên d?

A. (1; 3)    B. (0,4; 2,8)    C. ( 2,3; -1)    D. (4; -1,2)

Lời giải

+ Gọi H(a; b) là hình chiếu của M trên d.

+ Do H thuộc d nên 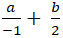 = 1 hay 2a - b = -2 (1)

+ Ta có: MH→(a; b - 3). Phương trình tổng quát (d): 2x - y + 2 = 0

Đường thẳng MH vuông góc d nên MH→ cùng phương n_d→(2; -1)

⇒  ⇔ -a = 2b - 6 hay a + 2b = 6 (2)

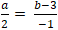
+ Từ (1) và (2) ta có hệ : 

⇒ Tọa độ điểm H(0,4; 2,8)

Chọn B.

Ví dụ 8: Cho đường thẳng d: x - y + 3 = 0 và điểm M(1; 1). Tìm hình chiếu của M trên d?

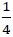
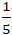
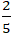
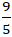
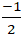
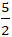
A. H(-  ;  ).    B. H( ;  ).    C. H( ;  ).    D. (4; -1)

Lời giải

+ Gọi H(a; b) là hình chiếu của M trên d.

+ Do H thuộc d nên a- b+3= 0 (1)

+ Ta có: MH→(a - 1; b - 1).

Đường thẳng MH vuông góc d nên MH→ cùng phương n_d→(1; -1)

⇒  ⇔ -a + 1 = b - 1 hay a + b = 2 (2)

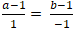
+ Từ (1) và (2) ta có hệ : 

⇒ Tọa độ điểm H( ;  ).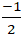

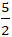
Chọn C.

Ví dụ 9: Cho đường thẳng d: 4x + y - 5 = 0 và điểm A(1; 1). Tìm hình chiếu của điểm A trên d?

A. (2; -1)    B. (-2; -1)    C. (1; 1)    D. (-1; 3)

Lời giải

Thay tọa độ điểm A vào phương trình đường thẳng d ta được :

4.1 + 1 - 5 = 0

⇒ Điểm A thuộc đường thẳng d nên hình chiếu của điểm A trên đường thẳng d là chính nó.

Chọn C.

Ví dụ 10: Cho đường thẳng (d): 2x + 3y - 3 = 0 và điểm M(0; 1) thuộc (d). Tập hợp những điểm A( x; y) sao cho M là hình chiếu của A trên d là đường thẳng nào?

A. 2x + 3y - 4 = 0    B. 3x - 2y + 2 = 0    C. 3x - 2y - 1 = 0    D. 2x - 3y + 3 = 0

Lời giải

+ Đường thẳng (d) có VTPT n→(2; 3).

+ Vecto MA→( x; y - 1).

Do M là hình chiếu của A trên d nên MA vuông góc d

⇒ Hai vecto MA→ và n→ cùng phương

⇔  ⇔ 3x = 2y - 2 hay 3x - 2y + 2 = 0

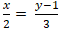
Vậy tập hợp những điểm A sao cho M là hình chiếu của A trên d là đường thẳng: ∆: 3x - 2y + 2 = 0

Chọn B.

Ví dụ 11: Cho đường thẳng d: x - y = 0 và điểm M(1; 3). Tìm hình chiếu của M trên d?

A. (1; 3)    B. (2; 2)    C. ( 3; -1)    D. (4; -1)

Lời giải

+ Gọi H(a;b) là hình chiếu của M trên d.

+ Do H thuộc d nên a - b = 0 (1)

+ Ta có: MH→(a - 1; b - 3).

Đường thẳng MH vuông góc d nên MH→ cùng phương n_d→ (1; -1)

⇒  ⇔ -a + 1= b - 3 hay a + b = 4 (2)

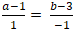
+ Từ (1) và (2) ta có hệ : 

⇒ Tọa độ điểm H(2; 2).

Chọn B