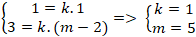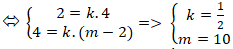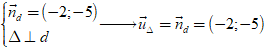Cách tìm vecto chỉ phương của đường thẳng

A. Phương pháp giải

+ Cho đường thẳng d, một vecto u→ được gọi là VTCP của đường thẳng d nếu u→ có giá song song hoặc trùng với đường thẳng d.

+ Nếu vecto u→( a; b) là VTCP của đường thẳng d thì vecto k.u→ ( với k ≠ 0) cũng là VTCP của đường thẳng d.

+ Nếu đường thẳng d có VTPT n→( a; b) thì đường thẳng d nhận vecto n→( b; -a) và n'→( - b;a) làm VTPT.

B. Ví dụ minh họa

Ví dụ 1. Đường thẳng d có một vectơ chỉ phương là u→ = (3; -4). Đường thẳng ∆ song song với d có một vectơ pháp tuyến là:

A. n₁→ = (4; 3)    B. n₂→ = (- 4; 3)    C. n₃→ = (3; 4)    D. n₄→ = (3; - 4)

Lời giải

Khi hai đường thẳng song song với nhau thì VTCP ( VTPT) của đường thẳng này cũng là VTCP (VTPT) của đường thẳng kia nên:

 → u_∆→ = u_d→ = (3; -4) → n_∆→ = (4; 3)

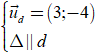
Chọn A

Ví dụ 2: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A(-3; 2) và B( 1; 4) ?

A. u₁→ = (-1; 2)    B. u₂→ = (2; 1)    C. u₃→ = (- 2; 6)    D. u₄→ = (1; 1)

Lời giải

+ Đường thẳng AB đi qua hai điểm A và B nên đường thẳng này nhận vecto AB→( 4; 2) làm vecto chỉ phương .

+ Lại có vecto AB→ và u→( 2;1) là hai vecto cùng phương nên đường thẳng AB nhận vecto u→( 2;1) là VTCP.

Chọn B.

Ví dụ 3: Vectơ chỉ phương của đường thẳng 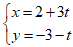 = 1 là:

A. u₄→ = (-2; 3)    B. u₂→ = (3; -2)    C. u₃→ = (3; 2)    D. u₁→ = (2; 3)

Hướng dẫn giải:

Ta đưa phương trình đường thẳng đã cho về dạng tổng quát:

 = 1 ⇔ 2x + 3y - 6 = 0 nên đường thẳng có VTPT là n→ = (2; 3)

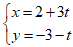
Suy ra VTCP là u→ = (3; - 2) .

Chọn B.

Ví dụ 4: Vectơ chỉ phương của đường thẳng d: 2x - 5y - 100 = 0 là :

A. u→ = (2; -5)    B. u→ = (2; 5)    C. u→ = (5; 2)    D. u→=( -5; 2)

Lời giải

Đường thẳng d có VTPT là n→( 2 ;- 5) .

⇒ đường thẳng có VTCP là u→( 5 ; 2).

Chọn C.

Ví dụ 5 : Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng đi qua hai điểm A(2 ; 3) và B( 4 ;1)

A. n→ = (2; -2)    B. n→ = (2; -1)    C. n→ = (1; 1)    D. n→ = (1; -2)

Lời giải

Đường thẳng AB nhận vecto AB→( 2; -2) làm VTCP nên đường thẳng d nhận vecto

n→( 1; 1) làm VTPT.

Chọn C.

Ví dụ 6. Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Ox

A. u₁→ = (1; 0).    B. u₂→ = (0; -1)    C. u₃→ = (1; 1)    D. u₄→ = (1; - 1)

Lời giải

Trục Ox có phương trình là y= 0; đường thẳng này có VTPT n→( 0;1)

⇒ đường thẳng này nhận vecto u→( 1; 0) làm VTCP.

⇒ một đường thẳng song song với Ox cũng có VTCP là u₁→=(1; 0).

Chọn A.

Ví dụ 7: Cho đường thẳng d đi qua A( 1; 2) và điểm B(2; m) . Tìm m để đường thẳng d nhận u→( 1; 3) làm VTCP?

A. m = - 2    B. m = -1    C. m = 5    D. m = 2

Lời giải

Đường thẳng d đi qua hai điểm A và B nên đường thẳng d nhận vecto AB→( 1; m - 2) làm VTCP.

Lại có vecto u→( 1; 2) làm VTCP của đường thẳng d. Suy ra hai vecto u→ và AB→ cùng phương nên tồn tại số k sao cho: u→ = kAB→

⇒ 

Vậy m= 5 là giá trị cần tìm .

Chọn C.

Ví dụ 8: Cho đường thẳng d đi qua A(- 2; 3) và điểm B(2; m + 1) . Tìm m để đường thẳng d nhận u→( 2; 4) làm VTCP?

A. m = - 2    B. m = -8    C. m = 5    D. m = 10

Lời giải

Đường thẳng d đi qua hai điểm A và B nên đường thẳng d nhận vecto AB→( 4; m - 2) làm VTCP.

Lại có vecto u→(2; 4) làm VTCP của đường thẳng d. Suy ra hai vecto u→ và ab→ cùng phương nên tồn tại số k sao cho: u→ = kAB→

Vậy m = 10 là giá trị cần tìm .

Chọn D.

Ví dụ 9. Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A( a; 0) và B( 0; b)

A. u→( -a; b)    B. u→( a; b)    C. u→( a + b; 0)    D. u→( - a; - b)

Lời giải

Đường thẳng AB đi qua điểm A và B nên đường thẳng này nhận AB→(-a;b) làm vecto chỉ phương.

Chọn A.

Ví dụ 10 . Đường thẳng d có một vectơ pháp tuyến là u→ = (-2; -5) . Đường thẳng ∆ vuông góc với d có một vectơ chỉ phương là:

A. u₁→ = (5; -2)    B. u₂→ = (-5; 2)    C. u₃→ = (2; 5)    D. u₄→ = (2; -5)

Lời giải

Khi hai đường thẳng vuông góc với nhau thì VTCP của đường thẳng này là VTPT của đường thẳng kia nên :

Lại có hai vecto u_∆→( -2; -5) và u→( 2;5) cùng phương nên đường thẳng ∆ nhận vecto u→( 2; 5) làm VTCP.

Chọn C.

Ví dụ 11: Vectơ chỉ phương của đường thẳng d 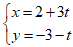 là:

A. u₁→ = (2; -3)    B. u₂→ = (3; -1)    C. u₃→ = (3; 1)    D. u₄→ = (3; -3)

Lời giải

Một VTCP của đường thẳng d là u→( 3; -1)

Chọn B