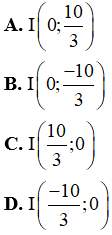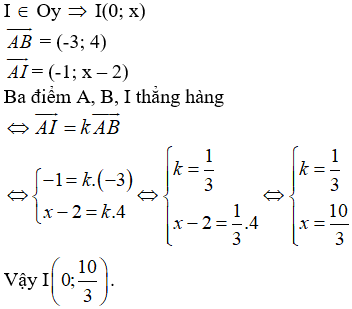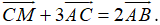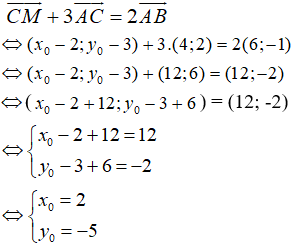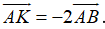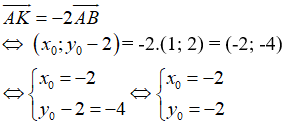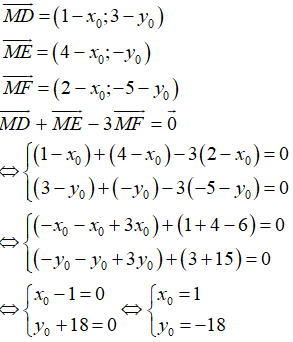Tìm tọa độ điểm thỏa mãn điều kiện cho trước cực hay, chi tiết
Tìm tọa độ điểm thỏa mãn điều kiện cho trước cực hay, chi tiết Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Tìm tọa độ điểm thỏa mãn điều kiện cho trước cực hay, chi tiết
Tìm tọa độ điểm thỏa mãn điều kiện cho trước cực hay, chi tiết
A. Phương pháp giải
Quy trình giải bài toán tìm tọa độ điểm thỏa mãn điều kiện cho trước:
Bước 1: Gọi tọa độ điểm cần tìm là M(x0; y0).
Bước 2: Thiết lập đẳng thức vecto hoặc mối quan hệ giữa điểm cần tìm và điểm đã biết…
Bước 3: Tọa độ hóa các vecto ở bước 2.
Bước 4: Thiết lập hệ phương trình theo các ẩn x0 và y0.
Bước 5: Giải hệ phương trình để tìm ra x0 và y0.
Bước 6: Kết luận.
B. Ví dụ minh họa
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho A(1; 2); B(-2; 6). Điểm I nằm trên trục Oy sao cho ba điểm A, B, I thẳng hàng thì tọa độ điểm I là:
Hướng dẫn giải:
Ta có:
Đáp án A
Ví dụ 2: Cho các điểm A(-2; 1), B(4; 0) và C(2; 3). Tìm điểm M biết rằng
Hướng dẫn giải:
Gọi tọa độ điểm M(x0; y0).
Ta có: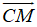 
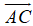
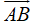
= (x0 - 2; y0 -3) , 
=(4; 2), 
=(6; -1)
Lại có
Vậy M (2; -5).
Ví dụ 3: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(0; 2) và B(1; 4). Tìm tọa độ điểm K thỏa mãn 
A. K(-2; -2)
B. K(1; -4)
C. K(3; 5)
D. K(0; -2)
Hướng dẫn giải:
Gọi tọa độ điểm K(x0; y0)
Ta có: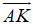 
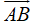
= (x0; y0 -2) và = (1; 2).
Vậy K(-2; -2).
Đáp án A
Ví dụ 4: Cho tam giác DEF có D(1; 3), E(4; 0) và F(2; -5). Tọa độ điểm M thỏa mãn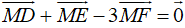 
là:
A. M(1; 18)
B. M(-1; 18)
C. M(-18; 1)
D. M(1; -18)
Hướng dẫn giải:
Gọi tọa độ điểm M(x0; y0)
Ta có:
Vậy M(1; -18).
Đáp án D
Ví dụ 5: Trong mặt phẳng tọa độ Oxy, cho A(2; 4), B(-1; 4) và C(-5; 1). Tìm tọa độ điểm D để tứ giác ABCD là hình bình hành.
A. D(-8; 1)
B. D(6; 7)
C. D(-2;1)
D. D(8; 1)
Hướng dẫn giải:
Gọi tọa độ điểm D(x0; y0).
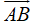
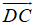
Ta có: = (-3; 0); 
=(-5 - x0; 1 - y0)
Tứ giác ABCD là hình bình hành
Vậy D(-2; 1)
Đáp án C
Bài viết liên quan
- Cách tìm tọa độ trung điểm của đoạn thẳng cực hay, chi tiết
- Cách tìm tọa độ của trọng tâm tam giác cực hay, chi tiết
- Cách tính độ dài vecto, khoảng cách giữa hai điểm trong hệ tọa độ cực hay, chi tiết
- Công thức, cách tính góc giữa hai vecto cực hay, chi tiết
- Cách chứng minh Hai vecto vuông góc cực hay, chi tiết
