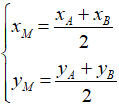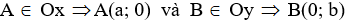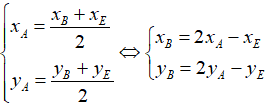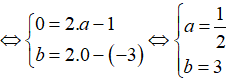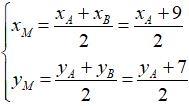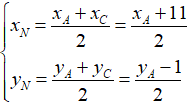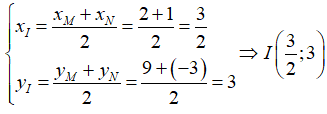A. Phương pháp giải

Áp dụng công thức tọa độ trung điểm của đoạn thẳng để giải bài tập.

Công thức tọa độ trung điểm của đoạn thẳng:

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(x_A; y_A) và B(x_B; y_B)

Nếu M là trung điểm của đoạn thẳng AB thì

B. Ví dụ minh họa

Ví dụ 1: Cho E(1; -3). Điểm 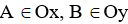 sao cho A là trung điểm của BE. Tọa độ điểm B là:

A. B(0; 3)

B. B(; 0)

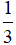
C. B(0; 2)

D. B(4; 2)

Hướng dẫn giải:

Ta có: 

Do A là trung điểm của BE nên ta có 

Vậy B(0; 3).

Đáp án A

Ví dụ 2: Ví dụ 2. Trong mặt phẳng tọa độ Oxy, cho điểm A(2; 3) và B(11; 5). Gọi H là điểm đối xứng của B qua A. Tọa độ điểm H là:

A. H (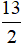; 4)

B. H(-7; 1)

C. H(7; -1)

D. H(20; 7)

Hướng dẫn giải:

Vì H là điểm đối xứng của B qua A, do đó A là trung điểm của BH.

Gọi tọa độ của H là H(x_H; y_H)

Áp dụng công thức tọa độ trung điểm ta có:

 H (-7; 1)

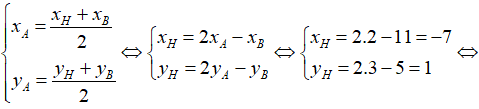
Đáp án B

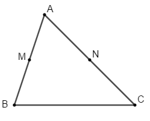
Ví dụ 3: Cho tam giác ABC, có B(9; 7) và C(11; -1). Gọi M và N lần lượt là trung điểm của AB và AC. Tọa độ vecto 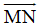 là: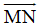

A. (2 ; -8)

B. 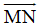(1; -4)

C. 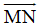(10; 6)

D. 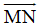(5; 3)

Hướng dẫn giải:

Do M là trung điểm của AB nên ta có: 

Do N là trung điểm của AC nên ta có: 

Tọa độ của 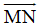 = (x_N; x_M; y_N; y_M)

Vậy 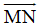 =(1; -4).

Ví dụ 4: Trong mặt phẳng tọa độ Oxy, gọi B’, B”, B”’ lần lượt là điểm đối xứng của B(-2; 7) qua trục Ox, Oy và qua gốc tọa độ O. Tọa độ các điểm B’, B”, B”’ là:

A. B’(-2; -7), B”(2; 7), B”’(2; -7)

B. B’(-7; 2), B”(2; 7), B”’(2; -7).

C. B’(-2; -7), B”(2; 7), B”’(-7; -2)

D. B’(-2; -7), B”(7; 2), B”’(2; -7).

Hướng dẫn giải:

+ B’ đối xứng với B(-2; 7) qua trục Ox, suy ra B’(-2; -7) (do đối xứng qua trục Ox thì hoành độ giữ nguyên và tung độ đối nhau).

+ B” đối xứng với B qua trục Oy, suy ra B”(2; 7) (do đối xứng qua trục Oy thì tung độ giữ nguyên và hoành độ đối nhau).

+ B”’ đối xứng với B qua gốc tọa độ O, suy ra O là trung điểm của BB”’

Nên ta có: 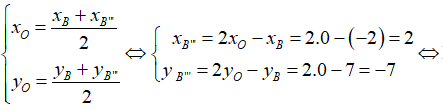 B”’(2; -7)

Ví dụ 5: Trong mặt phẳng tọa độ Oxy, cho hai điểm M(2; 9) và N(1; -3). Xác định tọa độ trung điểm I của đoạn thẳng MN.

Hướng dẫn giải:

Tọa độ trung điểm I của MN là