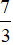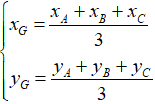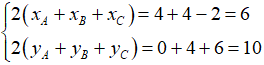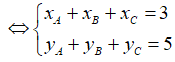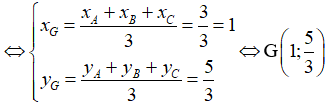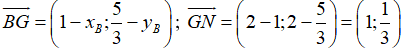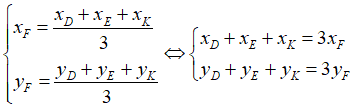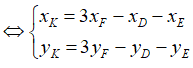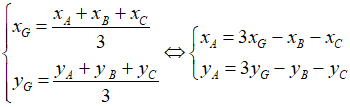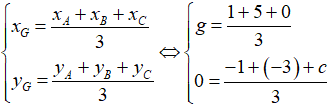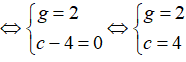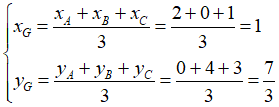A. Phương pháp giải

Áp dụng công thức tọa độ trọng tâm tam giác:

Cho tam giác ABC có A(x_A; y_A), B(x_B; y_B), C(x_C; y_C). Nếu G là trọng tâm của tam giác ABC thì:

B. Ví dụ minh họa

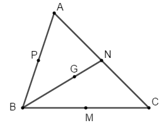
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M(2; 0) , N(2; 2), P(-1; 3) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tọa độ điểm B là:

A. B(1; 1)

B. B(1; -1)

C. B(-1;1)

D. B(-1; -1)

Hướng dẫn giải:

Gọi tọa độ của A(x_A; y_A), B(x_B; y_B), C(x_C; y_C)

M là trung điểm của BC nên ta có: 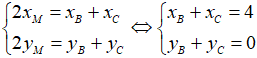 (1)

N là trung điểm của AC nên ta có: 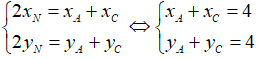 (2)

P là trung điểm của AB nên ta có: 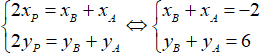 (3)

Từ (1), (2) và (3), cộng vế theo vế ta được: 

Gọi G là trọng tâm tam giác ABC

Suy ra tọa độ G: 

Ta có: 

 (do G là trọng tâm của tam giác ABC, N là trung điểm của AC)

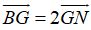
Suy ra: 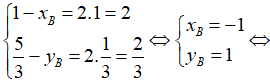 B(-1; 1)

Đáp án C

Ví dụ 2: Trong mặt phẳng tọa độ Oxy, cho tam giác DEF với tọa độ ba điểm D(-4;1), E(2; 4) và F(2; -2).

a, Tìm tọa độ trọng tâm H của tam giác DEF.

b, Tìm tọa độ điểm K sao cho F là trọng tâm tam giác DEK.

Hướng dẫn giải:

a, Tọa độ trọng tâm H của tam giác DEF là

 H (0; 1)

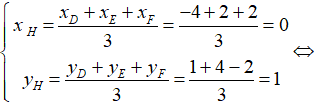
b, Gọi tọa độ K(x_K; y_K)

Vì F là trọng tâm tam giác DEK nên ta có:

Thay số ta được: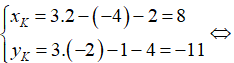 K (8; -11)

Ví dụ 3: Tam giác ABC có C(-2; -4), trọng tâm G(0; 4), trung điểm BC là M(2; 0). Tọa độ của đỉnh A và đỉnh B là:

A. A(4; 12), B(4; 6)

B. A(-4; -12), B(6; 4)

C. A(-4; 12), B(6; 4)

D. A(4; -12), B(-6; 4)

Hướng dẫn giải:

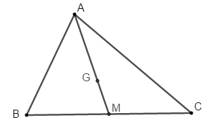
Vì M là trung điểm BC nên

  B (6; 4)

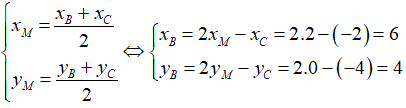
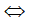
Vì G là trọng tâm tam giác ABC nên 

 A (-4; 12)

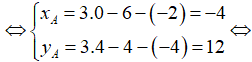
Đáp án C

Ví dụ 4: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; -1), B(5; -3) và C thuộc trục Oy, trọng tâm G của tam giác ABC nằm trên trục Ox. Tọa độ của điểm C là:

A. C(0; 4)

B. C(0; 2)

C. C(2; 0)

D. C(2; 4)

Hướng dẫn giải:

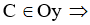
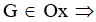
Ta có:  C(0; c)

 G(g; 0)

G là trọng tâm của tam giác ABC nên ta có:

Vậy C(0; 4).

Đáp án A

Ví dụ 5: Trong mặt phẳng tọa độ Oxy, cho các điểm A(2; 0), B(0; 4), C(1; 3).

a, Chứng minh rằng A, B, C là 3 đỉnh của một tam giác.

b, Tìm tọa độ trong tâm tam giác ABC.

Hướng dẫn giải:

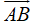
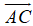
a, Ta có:  =(-2; 4) và  =(-1; 3)

Do 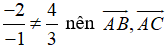 không cùng phương, suy ra A, B, C không thẳng hàng.

Vậy A, B, C là 3 đỉnh của một tam giác.

b, Gọi G là trọng tâm tam giác ABC. Suy ra tọa độ của G là:

Vậy tọa độ trọng tâm tam giác ABC là G (1; ).