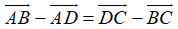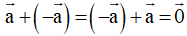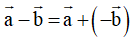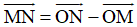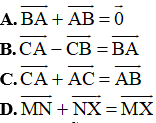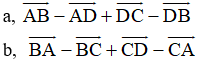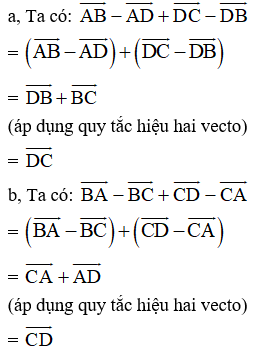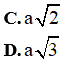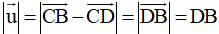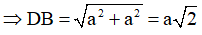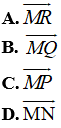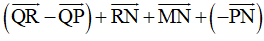Bài tập về hiệu của hai vecto cực hay, chi tiết
Bài tập về hiệu của hai vecto cực hay, chi tiết Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Bài tập về hiệu của hai vecto cực hay, chi tiết
Bài tập về hiệu của hai vecto cực hay, chi tiết
A. Phương pháp giải
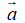
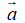
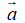
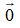
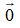
Vecto đối của một vecto: Vecto đối của vecto 
là vecto ngược hướng với và có cùng độ dài với vecto , ký hiệu là -
Vecto đối của vecto 
là vecto .
Vecto đối của vecto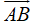 
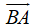
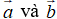
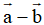
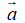
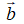
là vecto 
.
Hiệu hai vecto: Hiệu của hai vecto 
, kí hiệu là 
, là tổng của vecto và vecto đối của vecto 
, tức là
Phép lấy hiệu của hai vecto được gọi là phép trừ hai vecto.
Quy tắc về hiệu hai vecto: Nếu 
là một vecto đã cho thì với điểm O bất kỳ, ta luôn có
Phương pháp giải: áp dụng quy tắc về hiệu hai vecto, quy tắc ba điểm, vecto đối…
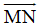
B. Ví dụ minh họa
Ví dụ 1: Cho các điểm A, B, C, M, N, X phân biệt. Chọn kết quả sai:
Hướng dẫn giải:
+ Ta có: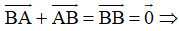 
A đúng
+ Lại có: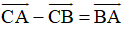 
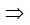
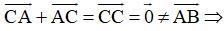
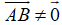
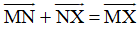
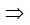
theo quy tắc hiệu hai vecto 
B đúng
+ 
C sai (vì A, B phân biệt nên 
)
+ 
theo quy tắc ba điểm D đúng
Đáp án C
Ví dụ 2: Cho tứ giác ABCD, tìm các vecto sau
Hướng dẫn giải:
Ví dụ 3: Cho hình vuông ABCD có cạnh là a. Độ dài của vecto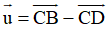 
là
A. a
B. 2a
Hướng dẫn giải:
Ta có: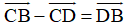 
(quy tắc về hiệu hai vecto)
Suy ra 
ABCD là hình vuông cạnh với đường chéo DB 
Vậy độ dài vecto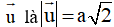 
.
Đáp án C
Ví dụ 4: Chỉ ra vecto tổng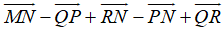 
trong các vecto sau
Hướng dẫn giải:
= 
= 
(áp dụng quy tắc hiệu hai vecto và vecto đối)
= 
(áp dụng quy tắc ba điểm)
= 
(tính chất giao hoán)
= 
(quy tắc ba điểm)
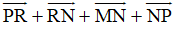
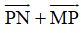
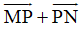
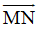
Vậy D đúng và A, B, C sai.
Đáp án D
Ví dụ 5: Cho 4 điểm A, B, C, D phân biệt. Chứng minh rằng
Hướng dẫn giải:
Ta có: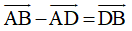 
(1) (áp dụng quy tắc về hiệu hai vecto)
Lại có: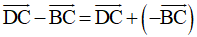 
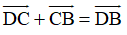
(vecto đối)
(2) (áp dụng quy tắc ba điểm về tổng hai vecto)
Từ (1) và (2) suy ra: (đpcm)
