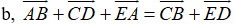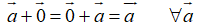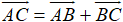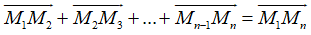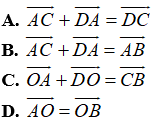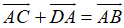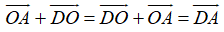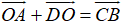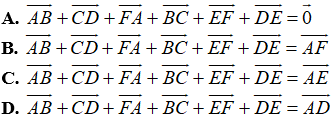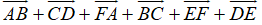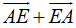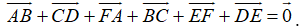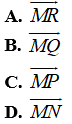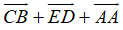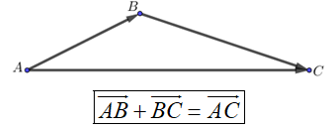
A. Phương pháp giải

 Định nghĩa: Cho hai vecto . Lấy một điểm A tùy ý ta vẽ , từ B vẽ . Vecto  được gọi là tổng của hai vecto . Kí hiệu: . Phép toán tìm tổng của hai vecto còn được gọi là phép cộng hai vecto.

 Các tính chất:

 Tính chất giao hoán: 

 Tính chất kết hợp: 

 Tính chất vecto-không: 

 Các quy tắc:

 Quy tắc 3 điểm: Cho 3 điểm A, B, C tùy ý ta có: 

 Quy tắc n điểm (mở rộng quy tắc 3 điểm): Cho n điểm , ta có:

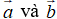
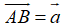
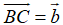
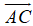
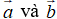
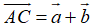
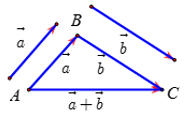
(quy tắc này được dùng để tìm tổng của nhiều vecto nối đuôi nhau)

 Phương pháp giải: Sử dụng linh hoạt các quy tắc và tính chất của phép cộng vecto để giải quyết bài tập.

B. Ví dụ minh họa

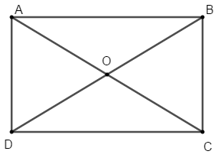
Ví dụ 1: Ví dụ 5. Cho hình chữ nhật ABCD tâm O, khẳng định nào sau đây là sai?

Hướng dẫn giải:

+ Ta có: 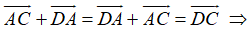 A đúng.

Lại có: ABCD là hình chữ nhật 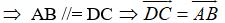 (hai vecto bằng nhau khi chúng có cùng hướng và cùng độ dài).

Do đó: 

Suy ra B đúng.

+ 

Mà 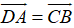 (Chứng minh tương tự )

Vậy 

Suy ra C đúng.

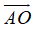
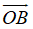
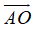
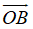
+ D sai vì vecto  và vecto  không cùng phương nên vecto  không thể bằng vecto .

Đáp án D

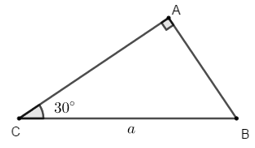
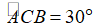
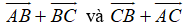
Ví dụ 2: Ví dụ 2. Cho tam giác ABC vuông tại A có  và BC = a. Tính độ dài vecto .

Hướng dẫn giải:

Nhận xét: để làm bài tập này, ta cần nhớ lại công thức độ dài vecto:

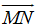
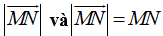
Độ dài của vecto , ký hiệu là .

Ví dụ 3: Ví dụ 3. Cho 6 điểm A, B, C, D, E, F. Đẳng thức nào sau đây đúng?

Hướng dẫn giải:

Ta có: 

=  (tính chất giao hoán và kết hợp)

=  (quy tắc 3 điểm)

= 

= .

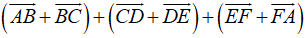
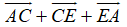
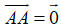
Vậy 

Suy ra A đúng, B, C, D sai.

Đáp án A

Ví dụ 4: Ví dụ 4. Chỉ ra vecto tổng của 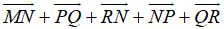 trong các vecto sau:

Hướng dẫn giải:

Đáp án D

Ví dụ 5: Ví dụ 1. Cho 5 điểm A, B, C, D, F. Chứng minh rằng

Hướng dẫn giải:

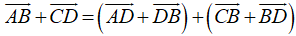
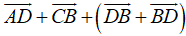
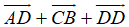
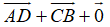
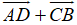
a, Ta có:  (áp dụng quy tắc 3 điểm)

=  (tính chất giao hoán kết hợp)

=  (quy tắc 3 điểm)

=  (nhớ lại khái niệm vecto-không là vecto có điểm đầu và điểm cuối trùng nhau)

=  (tính chất vecto-không)

Vậy 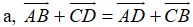 (đpcm)

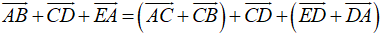
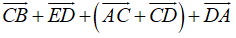
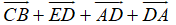
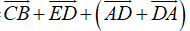
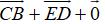
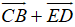
b, Ta có:  (áp dụng quy tắc 3 điểm)

= (áp dụng tính chất giao hoán và kết hợp)

=  (quy tắc 3 điểm)

=  (tính chất kết hợp)

= 

=  (vecto có điểm đầu và điểm cuối trùng nhau là vecto-không)

=  (tính chất vecto-không)

Vậy  (đpcm).