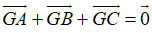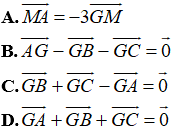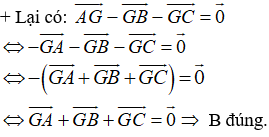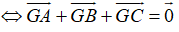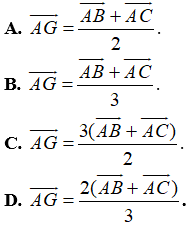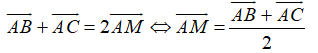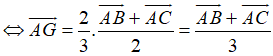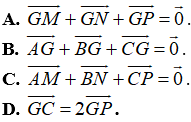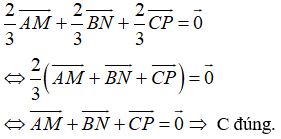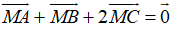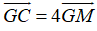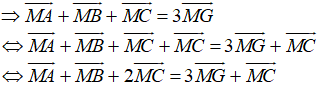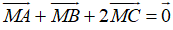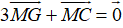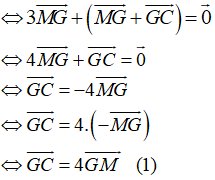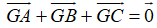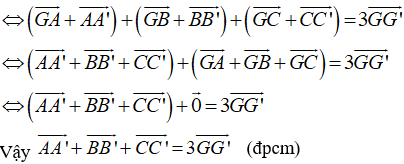A. Phương pháp giải

Trọng tâm tam giác là giao điểm của ba đường trung tuyến.

Áp dụng quy tắc trọng tâm tam giác:

Điểm G là trọng tâm tam giác ABC thì ta có:

  với mọi điểm M bất kỳ.

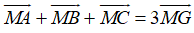
B. Ví dụ minh họa

Ví dụ 1: Điều kiện nào sau đây không phải là điều kiện cần và đủ để G là trọng tâm của tam giác ABC, với M là trung điểm của BC.

Hướng dẫn giải:

+ Ta có: 

 A, M, G thẳng hàng và  ngược hướng với vecto , do đó G nằm giữa M và A

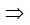
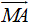
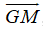
Mặt khác M là trung điểm BC và MA = 3GM ()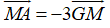

Vậy G là trọng tâm tam giác ABC 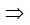 A đúng.

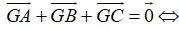
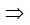
+ Ta có:  G là trọng tâm của tam giác ABC (theo lý thuyết)

 D đúng.

+ C sai, do nếu G là trọng tâm tam giác ABC 

Nên 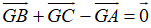 không phải là điều kiện để G là trọng tâm tam giác ABC.

Đáp án C

Ví dụ 2: Nếu G là trọng tâm tam giác ABC thì đẳng thức nào sau đây đúng?

Hướng dẫn giải:

Gọi M là trung điểm của BC nên ta có: 

Vì G là trọng tâm của tam giác ABC

Nên 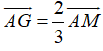 (tính chất trọng tâm trong tam giác)

Suy ra B đúng, A,C, D sai.

Đáp án B

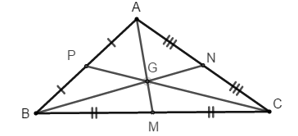
Ví dụ 3: Cho tam giác ABC có trọng tâm G. Gọi M, N, P lần lượt là trung điểm của BC, CA và AB. Chọn khẳng định sai?

Hướng dẫn giải:

+ Vì G là trọng tâm tam giác ABC và P là trung điểm của AC nên ta có GC = 2 GP mà vecto 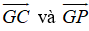 ngược hướng

Do đó: 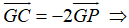 D sai.

Giải thích A, B, C đúng:

+ Do G là trọng tâm tam giác ABC

Suy ra B đúng.

+ Do M, N, P lần lượt là trung điểm của BC, CA, AB và G là trọng tâm của tam giác ABC

Thay vào (1) ta được:

thay vào (2) ta được:

Đáp án D

Ví dụ 4: Cho tam giác ABC có G là trọng tâm. Xác định điểm M sao cho:

A. Điểm M là trung điểm cạnh AC

B. Điểm M là trung điểm cạnh GC

C. Điểm M chia đoạn AB theo tỉ số 4

D. Điểm M chia đoạn GC thỏa mãn 

Hướng dẫn giải:

+ Do G là trọng tâm tam giác ABC và M là một điểm bất kỳ

Theo giả thiết ta lại có: 

Do đó ta được: 

Suy ra G, M, C thẳng hàng và M khác trung điểm của AB (2)

Vậy M chia đoạn GC thỏa mãn 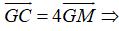 D đúng.

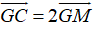
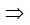
+ Từ (1) suy ra M khác trung điểm của GC (vì nếu M là trung điểm của GC thì  mâu thuẫn (1))  B sai.

+ Từ (2) suy ra A và C sai vì A, M, C không thẳng hàng, do đó M không thể là trung điểm AC và A, M , B không thẳng hàng nên M không thể chia AB theo tỷ số 4.

Đáp án D

Ví dụ 5: Cho G và G’ lần lượt là trọng tâm của hai tam giác ABC và A’B’C’. Chứng minh rằng .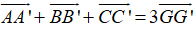

Hướng dẫn giải:

Do G là trọng tâm của tam giác ABC nên ta có: 

Do G’ là trọng tâm tam giác A’B’C’ và có điểm G nên ta có: