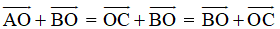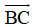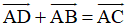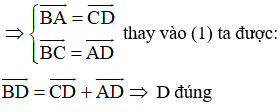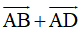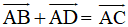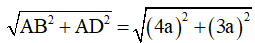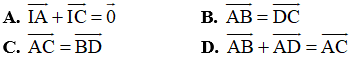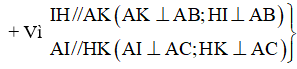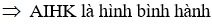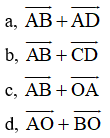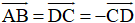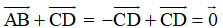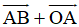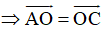Bài tập về Quy tắc hình bình hành của vecto cực hay, chi tiết
Bài tập về Quy tắc hình bình hành của vecto cực hay, chi tiết Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Bài tập về Quy tắc hình bình hành của vecto cực hay, chi tiết
Bài tập về Quy tắc hình bình hành của vecto cực hay, chi tiết
A. Phương pháp giải
Áp dụng quy tắc hình bình hành và các tính chất của hình hình hành đã học ở lớp 8 để giải bài tập.
|
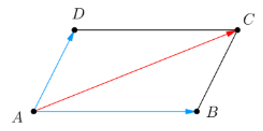
Quy tắc hình bình hành Nếu ABCD là hình bình hành thì ta có
Quy tắc này cũng đúng nếu ta xuất từ các đỉnh khác của hình bình hành. |
|
B. Ví dụ minh họa
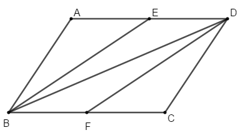
Ví dụ 1: Cho hình bình hành ABCD với E và F lần lượt là trung điểm của AD và BC. Khẳng định nào sau đây sai?
Hướng dẫn giải:
+ Ta có: ABCD là hình bình hành nên theo quy tắc hình bình hành ta được: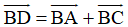 
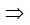
(1) 
A đúng
+ Lại có: ABCD là hình bình hành
Ví dụ 2: Cho hình chữ nhật ABCD có AB = 4a và AD = 3a. Tính độ dài 
Hướng dẫn giải:
ABCD là hình chữ nhật, suy ra ABCD cũng là hình bình hành, nên ta áp dụng quy tắc hình bình hành ta được: 
Suy ra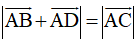 
= AC
Ta lại có: AC = 
Vậy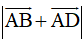 
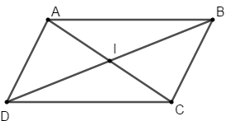
= 5a.
Ví dụ 3: Cho hình bình hành ABCD tâm I. Khẳng định nào sau đây là khẳng định sai?
Hướng dẫn giải:
+ Ta có I là tâm của hình bình hành ABCD nên I là trung điểm của AC
Do đó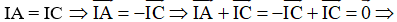 
đúng
+ Do ABCD là hình bình hành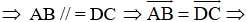 
đúng
+ AC và BD là hai đường chéo của hình bình hành nên chúng cắt nhau, do đó hai vecto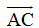 
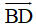
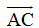
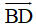
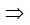
và 
không cùng phương nên vecto không thể bằng vecto (nhớ lại khái niệm hai vecto bằng nhau là cùng hướng và có độ dài bằng nhau) C sai
+ Ta có: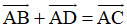 
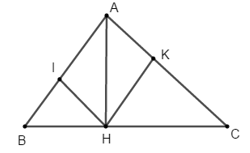
theo quy tắc hình bình hành D đúng
Ví dụ 4: Cho tam giác ABC vuông tại A, đường cao AH. Gọi I và K lần lượt là chân đường vuông góc hạ từ H lên AB và AC. Khẳng định nào sau đây là sai?
Hướng dẫn giải:
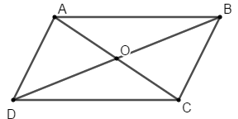
Ví dụ 5: Cho hình bình hành ABCD tâm O. Tính các vecto sau
Hướng dẫn giải:
a,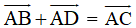 
theo quy tắc hình bình hành
b, Vì AB // CD nên ta có 
Do đó: 
c, 
= 
(sử dụng tính chất giao hoán)
= 
(quy tắc ba điểm)
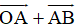
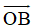
d,
Vì ABCD là hình bình hành tâm O nên O là trung điểm của AC
Suy ra AO = OC 
Ta có: 
(tính chất giao hoán)
= (quy tắc ba điểm)
