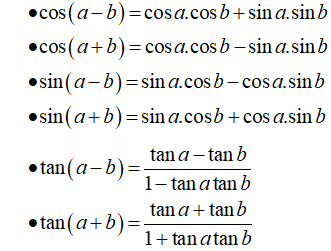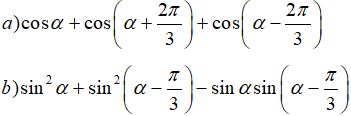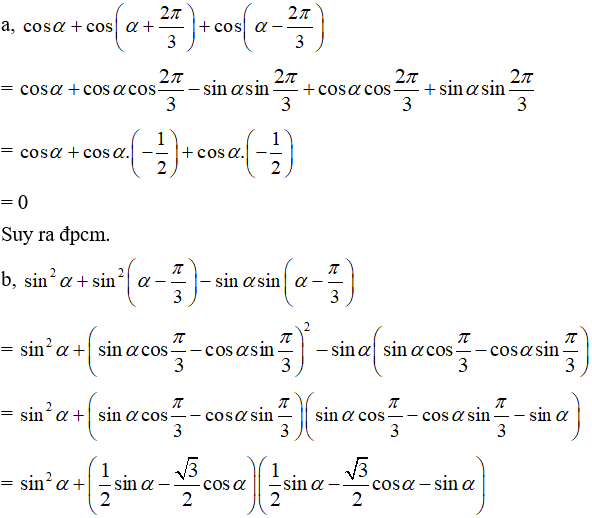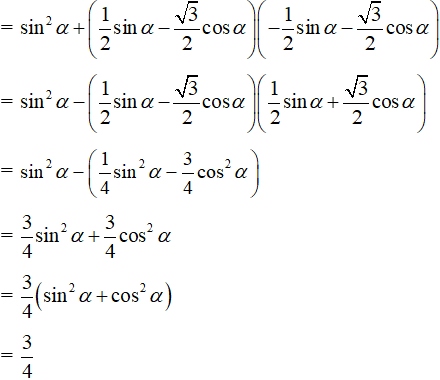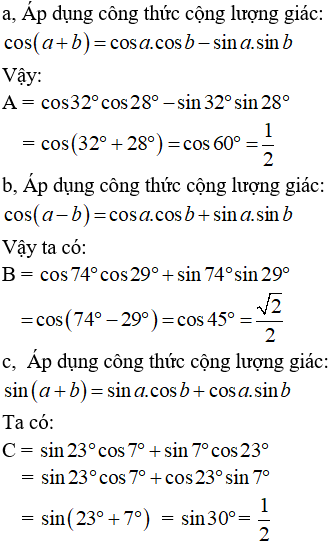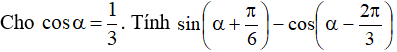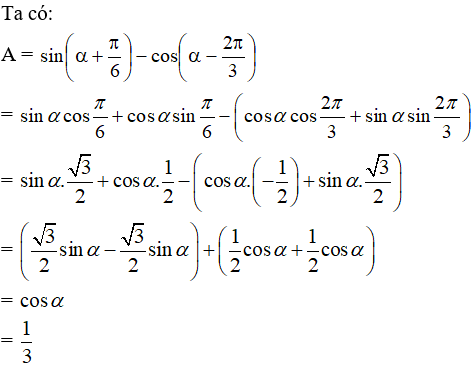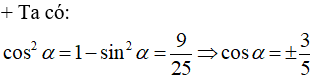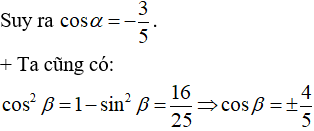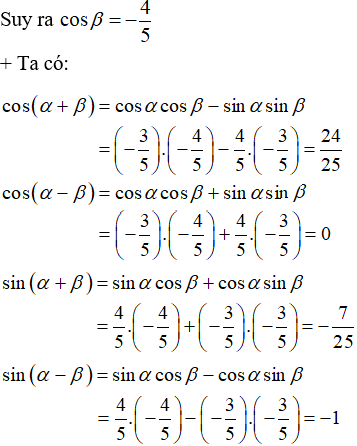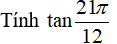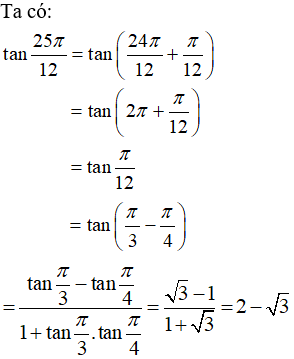Cách làm bài tập Công thức cộng lượng giác cực hay, chi tiếtv
Cách làm bài tập Công thức cộng lượng giác cực hay, chi tiết Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách làm bài tập Công thức cộng lượng giác cực hay, chi tiết
Cách làm bài tập Công thức cộng lượng giác cực hay, chi tiết
A. Phương pháp giải
Nhắc lại công thức cộng lượng giác:
Phương pháp giải: Áp dụng các công thức biến đổi trên.
B. Ví dụ minh họa
Ví dụ 1: Chứng minh các biểu thức sau luôn có giá trị không đổi, không phụ thuộc vào α.
Hướng dẫn giải:
Ví dụ 2: Tính giá trị các biểu thức
a, A = cos32ocos28o - sin32osin28o
b, B = cos74ocos29o + sin74osin29o
c, C = sin23ocos7o + sin7ocos23o
d, D = sin59ocos14o - sin14ocos59o
Hướng dẫn giải:
Ví dụ 3: 
Hướng dẫn giải:
Ví dụ 4: Cho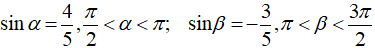 
. Tính cos(α + β), cos(α-β), sin(α + β), sin(α - β).
Hướng dẫn giải:
Vì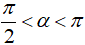 
nên điểm cuối của cung α thuộc góc phần tư thứ II, do đó cosα < 0
Vì 
nên điểm cuối của cung β thuộc góc phần tư thứ III, do đó cosβ < 0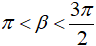
Ví dụ 5: 
Hướng dẫn giải:
Bài viết liên quan
- Giá trị lượng giác của các cung có liên quan đặc biệt cực hay, chi tiết
- Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại cực hay, chi tiết
- Cách giải bài tập Công thức nhân đôi lượng giác cực hay, chi tiết
- Chứng minh 2 vecto cùng phương, 2 vecto cùng hướng hay, chi tiết
- Bài tập về tổng của hai vecto cực hay, chi tiết
