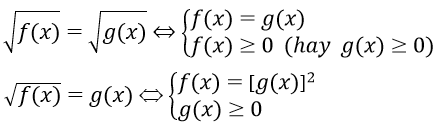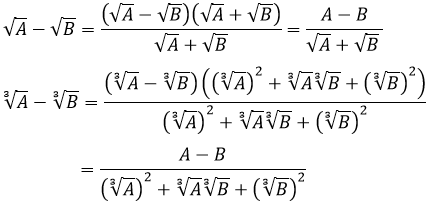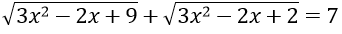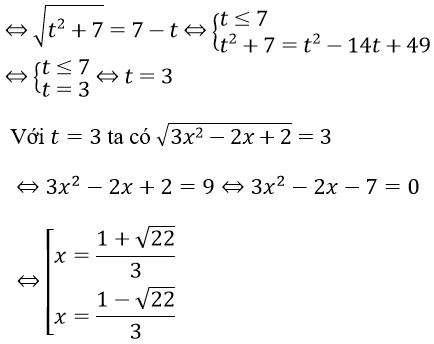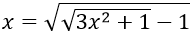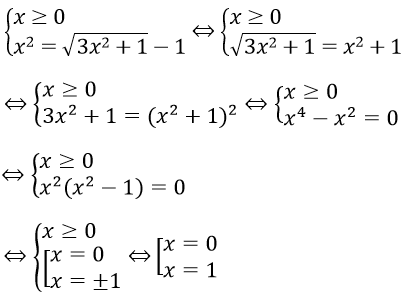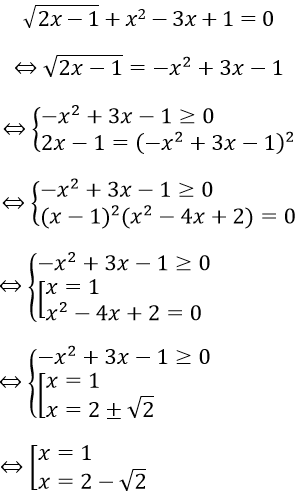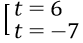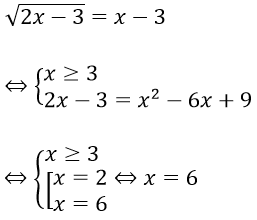Cách giải phương trình chứa ẩn dưới dấu căn cực hay, chi tiết
Cách giải phương trình chứa ẩn dưới dấu căn cực hay, chi tiết Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách giải phương trình chứa ẩn dưới dấu căn cực hay, chi tiết
Cách giải phương trình chứa ẩn dưới dấu căn cực hay, chi tiết
Lý thuyết & Phương pháp giải
Để giải phương trình chứa ẩn dưới dấu căn ta tìm cách để khử dấu căn, bằng cách:
– Nâng luỹ thừa hai vế.
– Phân tích thành tích.
– Đặt ẩn phụ.
Các dạng phương trình sau ta có thể giải bằng cách thực hiện phép biến đổi tương đương:
Phương trình có dạng a.f(x) + b.√(f(x) ) + c = 0 ta đặt √(f(x)) = t
Ngoài ra ta còn có phương pháp phân tích thành tích bằng cách nhân liên hợp
Với A, B không đồng thời bằng không
Ví dụ minh họa
Bài 1: Giải phương trình sau
Hướng dẫn:
Đặt t = √(3x2 - 2x + 2), điều kiện t ≥ 0. Khi đó √(3x2 - 2x + 9) = √(t2 + 7)
Phương trình trở thành √(t2 + 7) + t = 7
Vậy phương trình có hai nghiệm x = (1 ± √22)/3
Bài 2: Giải phương trình sau
Hướng dẫn:
Phương trình tương đương với phương trình
Vậy phương trình có nghiệm là x = 0 và x = 1
Bài 3: Giải phương trình sau √(2x-1) + x2 - 3x + 1 = 0
Hướng dẫn:
Ta có
Vậy phương trình có nghiệm là x = 1 và x = 2 - √2
Bài 4: Giải phương trình sau x2 + √(x2 + 11) = 31
Hướng dẫn:
Đặt t = √(x2 + 11), t ≥ 0. Khi đó phương trình đã cho trở thành:
t2 + t - 42 = 0 ⇔ 
Vì t ≥ 0 ⇒ t = 6, thay vào ta có √(x2 + 11) = 6
x2 + 11 = 36 ⇔ x = ±5
Vậy phương trình có nghiệm là x = ±5
Bài 5: Giải phương trình sau √(2x-3) = x-3
Hướng dẫn:
Ta có
Bài viết liên quan
- Cách giải phương trình chứa dấu giá trị tuyệt đối cực hay, chi tiết
- Cách giải phương trình chứa ẩn ở mẫu cực hay, chi tiết
- Các dạng phương trình quy về phương trình bậc hai đầy đủ, chi tiết
- Cách giải và biện luận hệ phương trình bậc nhất cực hay
- Cách giải các dạng hệ phương trình đặc biệt cực hay, chi tiết
