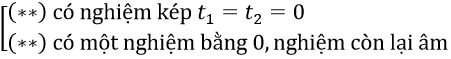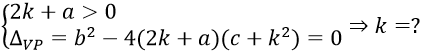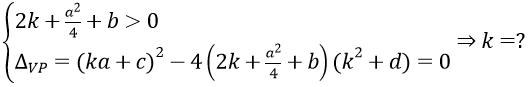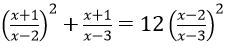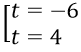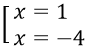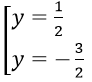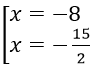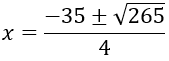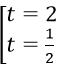Lý thuyết & Phương pháp giải

Phương trình trùng phương: ax⁴ + bx² + c = 0, (a ≠ 0) (*)

- Đặt t = x² ≥ 0 thì (*) ⇔ at² + bt + c = 0  (**)

- Để xác định số nghiệm của (*), ta dựa vào số nghiệm của (**) và dấu của chúng, cụ thể:

   + Để (*) vô nghiệm ⇔ 

   + Để (*) có 1 nghiệm

⇔ 

   + Để (*) có 2 nghiệm phân biệt ⇔ 

   + Để (*) có 3 nghiệm ⇔ (**) có 1 nghiệm bằng 0 và nghiệm còn lại dương.

   + Để (*) có 4 nghiệm ⇔ (**) có 2 nghiệm dương phân biệt.

Một số dạng phương trình bậc bốn quy về bậc hai

Loại 1. ax⁴ + bx³ + cx² + dx + e = 0 với e/a =(d/b)² ≠ 0

Phương pháp giải: Chia hai vế cho x² ≠ 0, rồi đặt t = x + α/x ⇒ t² = (x + α/x)² với α = d/b

Loại 2. (x+a)(x+b)(x+c)(x+d) = e với a + c = b + d

Phương pháp giải: [(x+a)(x+c)]⋅[(x+b)(x+d)] = e

⇔ [x² + (a+c)x + ac]⋅[x² + (b+d)x + bd] = e và đặt t = x² + (a+c)x

Loại 3. (x+a)(x+b)(x+c)(x+d) = ex² với a.b = c.d

Phương pháp giải: Đặt t = x² + ab + ((a+b+c+d)/2)x thì phương trình

⇔ (t + ((a+b-c-d)/2)x)(t - ((a+b-c-d)/2)x) = ex² (có dạng đẳng cấp)

Loại 4. (x+a)⁴ + (x+b)⁴ = c

Phương pháp giải: Đặt x = t-(a+b)/2 ⇒ (t + α)⁴ + (t - α)⁴ = c với α = (a-b)/2

Loại 5. x⁴ = ax² + bx + c (1)

Phương pháp giải: Tạo ra dạng A² = B² bằng cách thêm hai vế cho một lượng 2k.x² + k², tức phương trình (1) tương đương:

(x²)² + 2kx² + k² = (2k+a)x² + bx + c + k² ⇔ (x² + k)² = (2k + a)x² + bx + c + k²

Cần vế phải có dạng bình phương

⇒ 

Loại 6. x⁴ + ax³ = bx² + cx + d   (2)

Phương pháp giải: Tạo A² = B² bằng cách thêm ở vế phải 1 biểu thức để tạo ra dạng bình phương: (x² + (a/2)x + k)² = x⁴ + ax³ + (2k + a²/4)x² + kax + k². Do đó ta sẽ cộng thêm hai vế của phương trình (2) một lượng: (2k + a²/4)x² + kax + k², thì phương trình

(2)⇔ (x² + (a/2)x + k)² = (2k + (a²/4) + b)x² + (ka + c)x + k² + d

Lúc này cần số k thỏa:

Lưu ý: Với sự hổ trợ của casio, ta hoàn toàn có thể giải được phương trình bậc bốn bằng phương pháp tách nhân tử. Tức sử dụng chức năng table của casio để tìm nhân tử bậc hai, sau đó lấy bậc bốn chia cho nhân tử bậc hai, thu được bậc hai. Khi đó bậc bốn được viết lại thành tích của 2 bậc hai

Phân tích phương trình bậc ba bằng Sơ đồ Hoocner

Khi gặp bài toán chứa tham số trong phương trình bậc ba, ta thường dùng nguyên tắc nhẩm nghiệm sau đó chia Hoocner.

Nguyên tắc nhẩm nghiệm:

   + Nếu tổng các hệ số bằng 0 thì phương trình sẽ có 1 nghiệm x = 1

   + Nếu tổng các hệ số bậc chẵn bằng tổng các hệ số bậc lẻ thì PT có 1 nghiệm x = -1

   + Nếu phương trình chứa tham số, ta sẽ chọn nghiệm x sao cho triệt tiêu đi tham số m và thử lại tính đúng sai

Chia Hoocner: đầu rơi – nhân tới – cộng chéo

Ví dụ minh họa

Bài 1: Giải phương trình

Hướng dẫn:

Điều kiện: x ≠ 2; x ≠ 3

Đặt u = (x+1)/(x-2); v = (x-2)/(x-3) ta được u² + uv = 12v²

⇔(u - 3v)(u + 4v) = 0 ⇔ u = 3v; u = -4v

+) u = 3v ⇔ (x+1)/(x-2) = 3(x-2)/(x-3) ⇔ x² + 4x + 3 = 3x² - 12x + 12

⇔2x² - 16x + 9 = 0 ⇔ x = (8 ± √46)/2

+) u = -4v ⇔ (x+1)/(x-2) = -4(x-2)/(x-3) ⇔ x² + 4x + 3 = -4x² + 16x - 16

⇔ 5x² - 12x + 19 = 0(Vô nghiệm)

Vậy phương trình đã cho có hai nghiệm là x = (8 ± √46)/2

Bài 2: Giải phương trình x(x+1)(x+2)(x+3) = 24

Hướng dẫn:

Phương rình tương đương với (x² + 3x)(x² + 3x + 2) = 24

Đặt t = x² + 3x, phương trình trở thành

t(t+2) = 24 ⇔ t² + 2t - 24 = 0 ⇔

   + t = -6 ⇒ x² + 3x = -6 ⇔ x² + 3x + 6 = 0 (Phương trình vô nghiệm)

   + t = 4 ⇒ x² + 3x = 4 ⇔ x² + 3x - 4 = 0 ⇔

Vậy phương rình có nghiệm là x = -4 và x = 1

Hướng dẫn:

Phương trình tương đương với 4(x² + 17x + 60)(x² + 16x + 60) = 3x²  (*)

Ta thấy x = 0 không phải là nghiệm của phương trình.

Xét x ≠ 0, chia hai vế cho x² ta có

(*)⇔ 4(x + 17 + 60/x)(x + 16 + 60/x) = 3

Đặt y = x + 16 + 60/x phương trình trở thành

4(y+1)y = 3 ⇔ 4y² + 4y - 3 = 0 ⇔

Với y = 1/2 ta có x + 16 + 60/x = 1/2 ⇔ 2x² + 31x + 120 = 0

⇔

Với y = -3/2 ta có x + 16 + 60/x = -3/2 ⇔ 2x² + 35x + 120 = 0

⇔

Vậy phương trình có nghiệm là x = -8, x = -15/2 và

Bài 4: Giải phương trình (x+1)⁴ + (x+3)⁴ = 2

Hướng dẫn:

Đặt x = t - 2 phương trình trở thành (t-1)⁴ + (t+1)⁴ = 2 ⇔ t⁴ + 6t² = 0 ⇔ t²(t² + 6) = 0 ⇔ t = 0

Suy ra x = -2

Vậy phương trình có nghiệm duy nhất x = -2

Bài 5: Giải phương trình 2x⁴ - 5x³ + 6x² - 5x + 2 = 0

Hướng dẫn:

Ta thấy x = 0 không phải là nghiệm của phương trình nên chia hai vế phương trình cho x² ta được: 2(x² + 1/x²) - 5(x + 1/x) + 6 = 0

Đặt t = x + 1/x, ⇒ x² + 1/x² = (x + 1/x)² - 2 = t² - 2

Ta có phương trình: 2(t² - 2) - 5t + 6 = 0 ⇔ 2t² - 5t + 2 = 0 ⇔

   + t = 1/2 ⇒ x + 1/x = 1/2 ⇔ 2x² - x + 2 = 0 (vô nghiệm)

   + t = 2 ⇒ x + 1/x = 2 ⇔ x² - 2x + 1 = 0 ⇔ x = 1

Vậy phương trình có nghiệm duy nhất x = 1