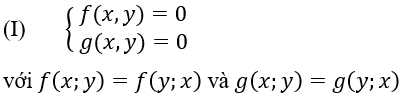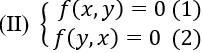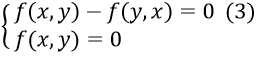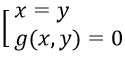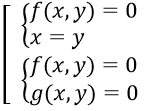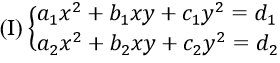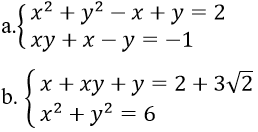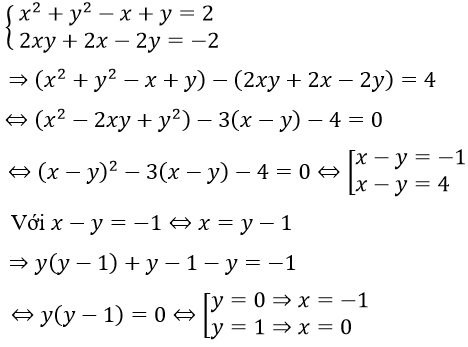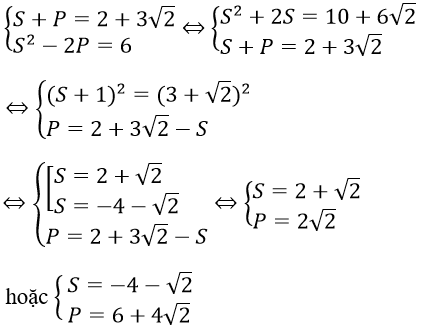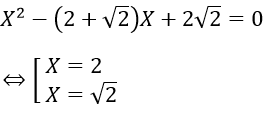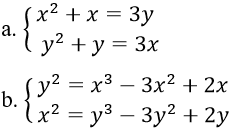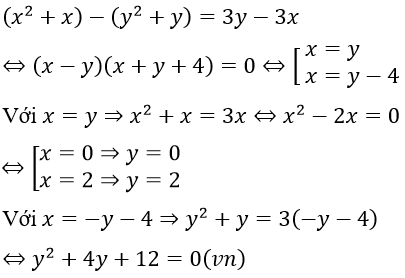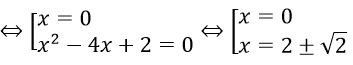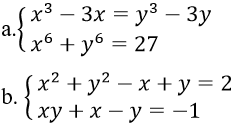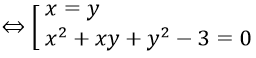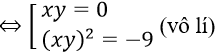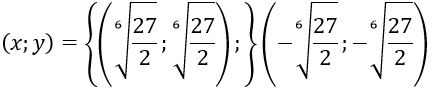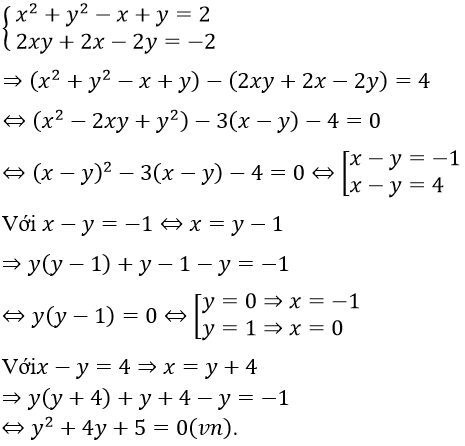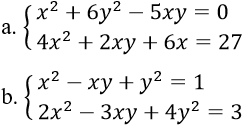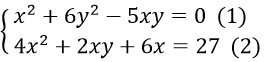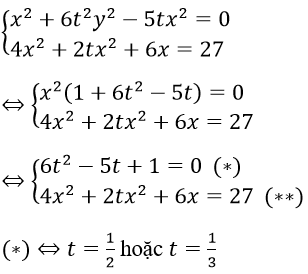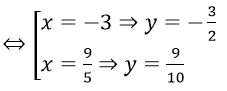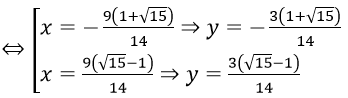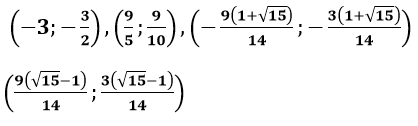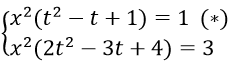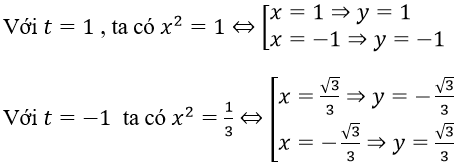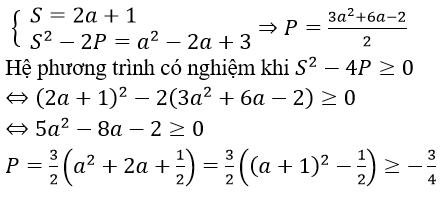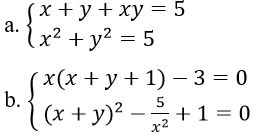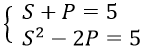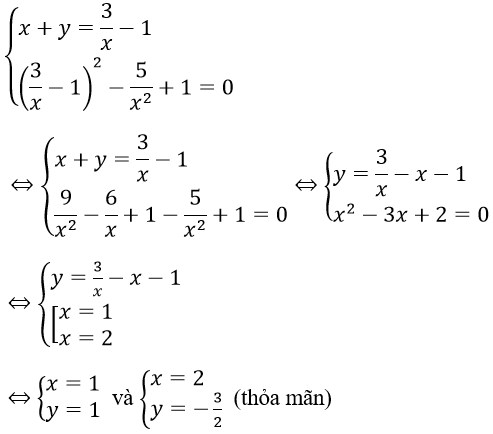Lý thuyết & Phương pháp giải

DẠNG TOÁN 1: HỆ GỒM MỘT PHƯƠNG TRÌNH BẬC NHẤT VÀ MỘT BẬC HAI

1. Phương pháp giải

Sử dụng phương pháp thế

- Từ phương trình bậc nhất rút một ẩn theo ẩn kia.

- Thế vào phương trình bậc hai để đưa về phương trình bậc hai một ẩn.

- Số nghiệm của hệ tuỳ theo số nghiệm của phương trình bậc hai này.

DẠNG TOÁN 2: HỆ PHƯƠNG TRÌNH ĐỐI XỨNG

1. Phương pháp giải

a. Hệ đối xứng loại 1

Hệ phương trình đối xứng loại 1 là hệ phương trình có dạng:

(Có nghĩa là khi ta hoán vị giữa x và y thì f(x, y) và g(x, y) không thay đổi).

Cách giải

- Đặt S = x + y, P = xy

- Đưa hệ phương trình (I) về hệ (I') với các ẩn là S và P.

- Giải hệ (I') ta tìm được S và P

- Tìm nghiệm (x; y) bằng cách giải phương trình: X² - SX + P = 0

b. Hệ đối xứng loại 2

Hệ phương trình đối xứng loại 2 là hệ phương trình có dạng:

(Có nghĩa là khi hoán vị giữa x và y thì (1) biến thành (2) và ngược lại)

- Trừ (1) và (2) vế theo vế ta được: (II) ⇔ 

- Biến đổi (3) về phương trình tích: (3) ⇔ (x-y).g(x,y) = 0 ⇔ 

- Như vậy (II) ⇔ 

- Giải các hệ phương trình trên ta tìm được nghiệm của hệ (II)

c. Chú ý: Hệ phương trình đối xứng loại 1, 2 nếu có nghiệm là (x₀; y₀) thì (y₀; x₀) cũng là một nghiệm của nó

DẠNG TOÁN 3: HỆ PHƯƠNG TRÌNH ĐẲNG CẤP BẬC HAI

1. Phương pháp giải

Hệ phương trình đẳng cấp bậc hai là hệ phương trình có dạng:

- Giải hệ khi x = 0 (hoặc y = 0)

- Khi x ≠ 0, đặt y = tx. Thế vào hệ (I) ta được hệ theo k và x. Khử x ta tìm được phương trình bậc hai theo k. Giải phương trình này ta tìm được k, từ đó tìm được (x; y)

Ví dụ minh họa

Bài 1: Xác định m để hệ phương trình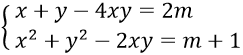có nghiệm

Hướng dẫn:

Hệ phương trình tương đương

(x² + y² - 2xy) - (x + y - 4xy) = m + 1 - 2m ⇔ (x+y)² - (x+y) + m - 1 = 0

Để hệ phương trình có nghiệm Δ ≥ 0 ⇔ 1 - 4(m-1) ≥ 0 ⇔ 5 - 4m ≥ 0

⇔ m ≤ 5/4

Từ phương trình thứ 2 ta có(x-y)² = m + 1 ⇒ m + 1 ≥ 0 ⇔ m ≥ -1

Do đó -1 ≤ m ≤ 5/4

Bài 2: Giải hệ phương trình

Hướng dẫn:

a. Hệ phương trình tương đương

Với x-y = 4 ⇒ x = y + 4 ⇒ y(y+4) + y + 4 - y = -1

⇔ y² + 4y + 5 = 0 (vn)

Vậy nghiệm của hệ phương trình là (x; y) = {(0; 1), (-1; 0)}

b. Đặt S = x+y; P = xy, ta có hệ:

- Với S = 2 + √2; P = 2√2 ta có x, y là nghiệm phương trình:

Với S = -4-√2; P = 6 + 4√2 ta có x, y là nghiệm phương trình:

X² + (4+√2)X + 6 + 4√2 = 0 (vô nghiệm)

Vậy hệ có nghiệm (x; y) là (2; √2) và (√2; 2)

Bài 3: Giải hệ phương trình

Hướng dẫn:

a. Hệ phương trình tương đương

Vậy tập nghiệm của hệ phương trình là: (x; y) = {(0;0), (2;2)}

b. Trừ vế với vế của phương trình đầu và phương trình thứ hai ta được:

(y² - x² = x³ - y³ - 3(x² - y²) + 2(x-y) ⇔ (x-y)(x² + xy + y² - 2x - 2y + 2) = 0 ⇔ 1/2(x-y)[x² + y² + (x + y - 2)²] = 0 ⇔ x = y)

(vì x² + y² + (x+y-2)² > 0)

Thay x = y vào phương trình đầu ta được:

x³ - 4x² + 2x = 0 ⇔ x(x² - 4x + 2) = 0

Vậy hệ phương trình có ba nghiệm: (0; 0); (2+√2; 2+√2) và (2-√2; 2-√2)

Bài 4: Giải hệ phương trình

Hướng dẫn:

a. Ta có : x³ - 3x = y³ - 3y ⇔ (x-y)(x² + xy + y²) - 3(x-y) = 0

⇔ (x-y)(x² + xy + y² - 3) = 0

Khi x = y thì hệ có nghiệm

Khi x² + xy + y² - 3 = 0 ⇔ x² + y² = 3 - xy, ta có x⁶ + y⁶ = 27

⇔ (x² + y²)(x⁴ - x²y² + y⁴) = 27

⇒ (3-xy)[(3-xy)² - 3x²y²] = 27 ⇔ 3(xy)³ + 27xy = 0

Vậy hệ phương trình đã cho có 2 nghiệm

b. Hệ phương trình tương đương

Bài 5: Giải hệ phương trình

Hướng dẫn:

a. Ta có

Nếu x = 0 thay vào (1)⇒ y = 0, thay vào (2) thấy (x; y) = (0; 0) là nghiệm

của phương trình (2) nên không phải là nghiệm của hệ phương trình

Nếu x ≠ 0, đặt y = tx , thay vào hệ ta được

Với t = 1/2 thay vào (**) ta được 4x² + x² + 6x = 27 ⇔ 5x² + 6x - 27 = 0

Với t = 1/3 thay vào (**) ta được 4x² + (2/3)x² + 6x = 27

⇔ 14x² + 18x - 81 = 0

Vậy hệ phương trình có nghiệm (x; y) là:

b. Dễ thấy x = 0 không thoả hệ

Với x ≠ 0, đặt y = tx, thay vào hệ ta được

Suy ra 3(t² - t + 1) = 2t² - 3t + 4 ⇒ t = ±1

Thay vào (*) thì

Vậy hệ phương trình có nghiệm (x; y) là (1/√3;(-1)/√3), ((-1)/√3;1/√3), (-1;-1) và (1;1)

Bài 6: Cho hệ phương trình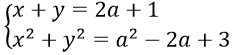. Tìm giá trị thích hợp của tham số a sao cho hệ có nghiệm (x; y) và tích x.y nhỏ nhất.

Hướng dẫn:

Đặt S = x + y, P = xy (S² - 4P ≥ 0)

Ta có

Đẳng thức xảy ra khi a = -1 (nhận)

Bài 7: Giải hệ phương trình

Hướng dẫn:

a. Đặt S = x + y, P = xy (S² - 4P ≥ 0)

Ta có : 

⇒S² - 2(5-S) = 5 ⇒ S² + 2S - 15 = 0

⇒ S = -5; S = 3

S = -5⇒ P = 10 (loại)

S = 3⇒ P = 2(nhận)

Khi đó : x, y là nghiệm của phương trình X² - 3X + 2 = 0

⇔ X = 1; X = 2

Vậy hệ có nghiệm (2; 1), (1; 2)

b. ĐKXĐ: x ≠ 0

Hệ phương trình tương đương với

Vậy hệ phương trình có nghiệm (x; y) là (1; 1) và (2; -3/2)