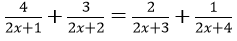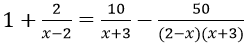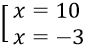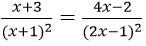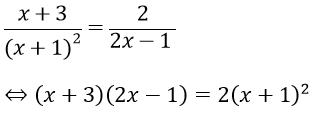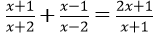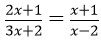Cách giải phương trình chứa ẩn ở mẫu cực hay, chi tiết
Cách giải phương trình chứa ẩn ở mẫu cực hay, chi tiết Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách giải phương trình chứa ẩn ở mẫu cực hay, chi tiết
Cách giải phương trình chứa ẩn ở mẫu cực hay, chi tiết
Lý thuyết & Phương pháp giải
Để giải phương trình chứa ẩn ở mẫu ta thường
- Quy đồng mẫu số (chú ý cần đặt điều kiện mẫu số khác không)
- Đặt ẩn phụ
Ví dụ minh họa
Bài 1: Giải phương trình
Hướng dẫn:
ĐKXĐ: x ∉ {-2; -3/2; -1; -1/2}
Phương trình tương đương với
Vậy phương trình có nghiệm là x = (-5 ± √3)/4 và x = -5/2
Bài 2: Giải phương trình 
Hướng dẫn:
ĐKXĐ: x ≠ -3 và x ≠ 2
Phương trình tương đương với (2 - x)(x + 3) - 2(x + 3) = 10(2 - x) - 50
⇔ x2 - 7x - 30 = 0 ⇔ 
Đối chiếu với điều kiện ta có nghiệm của phương trình là x = 10
Bài 3: Giải phương trình 
Hướng dẫn:
ĐKXĐ: x ≠ -1 và x ≠ 1/2
Phương trình tương đương với
⇔ x = 5 (thỏa mãn điều kiện)
Vậy phương trình có nghiệm là x = 5
Bài 4: Giải phương trình 
Hướng dẫn:
ĐKXĐ: x≠±2 và x≠-1
Phương trình tương đương với
(x+1)2(x-2) + (x-1)(x+1)(x+2) = (2x+1)(x-2)(x+2)
⇔ (x2 + 2x + 1)(x - 2) + (x2 - 1)(x + 2) = (2x + 1)(x2 - 4)
⇔ x3 - 2x2 + 2x2 - 4x + x - 2 + x3 + 2x2 - x - 2 = 2x3 - 8x + x2 - 4
⇔ x2 + 4x = 0 ⇔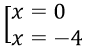
(thỏa mãn điều kiện)
Vậy phương trình có nghiệm là x = -4 và x = 0
Bài 5: Giải phương trình
Hướng dẫn:
ĐKXĐ: x ≠ -2/3 và x ≠ 2
Phương trình tương đương với (2x+1)(x-2) = (x+1)(3x+2)
⇔ 2x2 - 4x + x - 2 = 3x2 + 2x + 3x + 2
⇔ x2 + 8x + 4 = 0 ⇔ x = -4 ± 2√3 (thỏa mãn điều kiện)
Vậy phương trình có nghiệm là x = -4 ± 2√3
