Giải bài tập Toán lớp 6 Bài 9: Dấu hiệu chia hết

Video giải Toán 6 Bài 9: Dấu hiệu chia hết - Kết nối tri thức

Hoạt động 1 trang 34 Toán lớp 6 Tập 1: Số 230 có chia hết cho 2 và chia hết cho 5 không?

Lời giải:

Ta có:

230 : 2 = 115 nên 230 chia hết cho 2

230 : 5 = 46 nên 230 chia hết cho 5

Vậy 230 chia hết cho cả 2 và 5.

Hoạt động 2 trang 34 Toán lớp 6 Tập 1: Xét $\mathrm{n}=\overline{23*}$ (* là chữ số tận cùng của n). Ta viết $\mathrm{n}=230+*$

Vận dụng tính chất chia hết của một tổng, hãy cho biết:

a) Thay dấu * bởi chữ số nào thì n chia hết cho 2?

b) Thay dấu * bởi chữ số nào thì n chia hết cho 5?

Lời giải:

a) $\mathrm{n}=230+*$ (* là chữ số tận cùng của n,$*\in \mathrm{\mathbb{N}}$ ; $0\le *\le 9$)

Để $n⋮2$ hay (230+*) $⋮2$ mà $230⋮2$ nên $*⋮2$

Lại có $0\le *\le 9$ do đó $*\in \text{{}0;2;4;6;8\}$

b) $\mathrm{n}=230+*$ (* là chữ số tận cùng của n,$*\in \mathrm{\mathbb{N}}$ ; $0\le *\le 9$)

Để $n⋮5$ hay (230+*) $⋮5$ mà $230⋮5$ nên $*⋮5$

Lại có $0\le *\le 9$ do đó $*\in \text{{}0;5\}$.

Luyện tập 1 trang 35 Toán lớp 6 Tập 1: (1) Không thực hiện phép tính, em hãy cho biết tổng (hiệu) sau có chia hết cho 2 không.

a) 1 954 + 1 975 

b) 2 020 – 938

(2) Không thực hiện phép tính, em hãy cho biết tổng (hiệu) sau có chia hết cho 5 không.

a) 1 945 + 2 020                         

b) 1 954 – 1 930

Lời giải:

(1)

a) Số 1 954 có chữ số tận cùng là 4 nên chia hết cho 2; số 1 975 có chữ số tận cùng là 5 nên không chia hết cho 2.

Vậy tổng 1 954 + 1 975 không chia hết cho 2.

b) Số 2 020 có chữ số tận cùng là 0 nên chia hết cho 2; số 938 có chữ số tận cùng là 8 nên chia hết cho 2.

Vậy hiệu 2 020 - 938 chia hết cho 2.

(2)

a) Số 1 945 có chữ số tận cùng là 5 nên chia hết cho 5; số 2 020 có chữ số tận cùng là 0 nên chia hết cho 5.

Vậy tổng 1 945 + 2 020 chia hết cho 5.

b) Số 1 954 có chữ số tận cùng là 4 nên không chia hết cho 5; số 1 930 có chữ số tận cùng là 0 nên chia hết cho 5.

Vậy hiệu 1 954 - 1 930 không chia hết cho 5.

Hoạt động 3 trang 35 Toán lớp 6 Tập 1: Cho các số 27; 82; 195; 234.

Hãy sắp xếp các số trên thành hai nhóm: Nhóm các số chia hết cho 9 và nhóm các số không chia hết cho 9.

Lời giải:

Ta có: 27: 9 = 3; 82 : 9 = 9 (dư 1); 195 : 9 = 21 (dư 6); 234 : 9 = 26

+) Các số chia hết cho 9 là: 27; 234

+) Các số không chia hết cho 9 là: 82; 195

Hoạt động 4 trang 35 Toán lớp 6 Tập 1: Cho các số 27; 82; 195; 234.

Tính tổng các chữ số của mỗi số và xét tính chia hết cho 9 của các tổng đó trong mỗi nhóm.

Lời giải:

* Xét nhóm các số chia hết cho 9 là: 27; 234

+) Xét số 27 có tổng các chữ số là: 2 + 7 = 9, vì $9⋮9$ nên $(2+7)⋮9$

+) Xét số 234 có tổng các chữ số là: 2 + 3 + 4 = 9, vì $9⋮9$ nên $(2+3+4)⋮9$

* Xét nhóm các số không chia hết cho 9 là: 82; 195

+) Xét số 82 có tổng các chữ số là: 8 + 2 = 10, vì $10\cancel{⋮}9$ nên $(8+2)\cancel{⋮}9$

+) Xét số 195 có tổng các chữ số là: 1 + 9 + 5 = 15, vì $15\cancel{⋮}9$ nên $(1+9+5)\cancel{⋮}9$

Luyện tập 2 trang 35 Toán lớp 6 Tập 1: Thay dấu * bởi một chữ số để được số $\overline{12*}$ chia hết cho 9.

Lời giải:

Vì số $\overline{12*}$ chia hết cho 9 thì tổng các chữ số của nó cũng chia hết cho 9

Nên (1 + 2 + *) chia hết cho 9 hay (3 + *) chia hết cho 9

Vì * là chữ số hàng đơn vị của số $\overline{12*}$ nên $*\in \mathrm{\mathbb{N}}$;  $0\le *\le 9$

Vậy * là 6 ta được số 126.

Vận dụng trang 36 Toán lớp 6 Tập 1: Trên một bờ đất dài 108m, một bác nông dân có kế hoạch trồng một số cây dừa thành một hàng sao cho hai cây cách đều nhau là 9m và luôn có cây ở vị trí đầu và cuối của bờ đất. Hỏi bác nông dân có trồng được như vậy không? Nếu được, bác cần bao nhiêu cây dừa để trồng?

Lời giải:

Ta thấy 108 có tổng các chữ số là 1 + 0 + 8 = 9 $⋮$ 9 nên 108 $⋮$ 9

Mà hai cây cách đều nhau 9m vì thế mà bác nông dân trồng được như vậy.

Vì cứ 2 cây dừa liên tiếp có 1 khoảng cách là 9m, 3 cây dừa liên tiếp có 2 khoảng cách,… nên số các khoảng cách giữa hai cây liên tiếp là:

108 : 9 = 12 (khoảng cách)

Số cây dừa bác cần để trồng là:

12 + 1 = 13 (cây)

Vậy bác cần trồng 13 cây dừa.

Hoạt động 5 trang 36 Toán lớp 6 Tập 1: Cho các số 42; 80; 191; 234.

Hãy sắp xếp các số trên thành hai nhóm: Nhóm các số chia hết cho 3 và nhóm các số không chia hết cho 3.

Lời giải:

Ta có: 42 : 3 = 14; 80 : 3 = 26 (dư 2); 191 : 3 = 63 (dư 2); 234 : 3 = 78

+) Các số chia hết cho 3 là: 42; 234

+) Các số không chia hết cho 3 là: 80; 191

Hoạt động 6 trang 36 Toán lớp 6 Tập 1: Cho các số 42; 80; 191; 234.

Tính tổng các chữ số của mỗi số và xét tính chia hết cho 3 của các tổng đó trong mỗi nhóm.

Lời giải:

*Xét nhóm các số chia hết cho 3 là: 42; 234

+) Xét số 42 có tổng các chữ số là: 4 + 2 = 6, vì $6⋮3$ nên $(4+2)⋮3$

+) Xét số 234 có tổng các chữ số là: 2 + 3 + 4 = 9, vì $9⋮3$ nên $(2+3+4)⋮3$

*Xét nhóm các số không chia hết cho 3 là: 80; 191

+) Xét số 80 có tổng các chữ số là: 8 + 0 = 8, vì $8\cancel{⋮}3$ nên $(8+0)\cancel{⋮}3$

+) Xét số 191 có tổng các chữ số là: 1 + 9 + 1 = 11, vì $11\cancel{⋮}3$ nên $(1+9+1)\cancel{⋮}3$

Luyện tập 3 trang 36 Toán lớp 6 Tập 1: Thay dấu * bằng một chữ số để số $\overline{12*5}$ chia hết cho 3.

Lời giải:

Để $\overline{12*5}$ chia hết cho 3 thì tổng các chữ số của nó cũng chia hết cho 3 nên

(1 + 2 + * + 5) chia hết cho 3 hay (8 + *) chia hết cho 3

Vì * là chữ số ở hàng chục của $\overline{12*5}$ nên $*\in \mathrm{\mathbb{N}}$; $0\le *\le 9$

Do đó: $*\in \text{{}1;4;7\}$. Khi đó ta có các số: 1 215; 1 245; 1 275

Vậy $*\in \text{{}1;4;7\}$.

Thử thách nhỏ trang 36 Toán lớp 6 Tập 1: Bạn Hà cần tìm đường đến siêu thị. Biết rằng Hà chỉ có thể đi qua ô có chứa số chia hết cho 2 hoặc chia hết cho 3 và mỗi ô chỉ đi qua một lần. Em hãy giúp Hà đến được siêu thị nhé.

Lời giải:

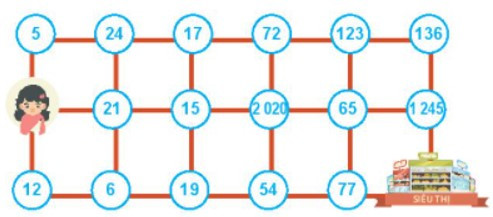
Vì Hà chỉ có thể đi qua ô chứa số chia hết cho 2 hoặc 3 nên Hà không thể đi qua các ô số:

5; 17; 19; 65; 77 vì các ô số này đều không chia hết cho 2 và 3.

Có nhiều cách để Hà đi đến siêu thị, dưới đây là 2 cách:

Cách 1: Hà $\to$ 21 $\to$15 $\to$ 2020 $\to$ 72 $\to$ 123 $\to$ 136 $\to$ 1245 $\to$ siêu thị

Cách 2: Hà $\to$12 $\to$ 6 $\to$ 21 $\to$ 15 $\to$ 2020 $\to$ 72 $\to$ 123 $\to$ 136 $\to$ 1245 $\to$siêu thị

Bài 2.10 trang 37 Toán lớp 6 Tập 1: Trong các số sau, số nào chia hết cho 2, số nào chia hết cho 5?

324; 248; 2 020; 2025.

Lời giải:

+) Vì các số 324; 248; 2 020 có chữ số tận cùng lần lượt là 4; 8; 0

nên 324; 248; 2 020 chia hết cho 2

+) Vì các số 2 020; 2025 có chữ số tận cùng lần lượt là 0 và 5

nên 2 020; 2025 chia hết cho 5.

450 ; 123 ; 2 019 ; 2 025.

Lời giải:

+) Xét số 450 có tổng các chữ số 4 + 5 + 0 = 9, vì 9 $⋮3$ và 9$⋮9$ nên 450 $⋮$ 3 và 450 $⋮$ 9.

+) Xét số 123 có tổng các chữ số 1 + 2 + 3 = 6, vì 6 $⋮$ 3 và 6 $\cancel{⋮}$9 nên 123$⋮$ 3 và 123$\cancel{⋮}$ 9

+) Xét số 2 019 có tổng các chữ số 2 + 0 + 1 + 9 = 12, vì 12$⋮$3 và 12 $\cancel{⋮}$9 nên 2 019$⋮$ 3 và

2 019 $\cancel{⋮}$9

+) Xét số 2 025 có tổng các chữ số 2 + 0 + 2 + 5 = 9, vì 9$⋮3$ và 9$⋮9$ nên 2 025 $⋮$ 3 và

2 025 $⋮$ 9.

Vậy các số chia hết cho 3 là: 450; 123; 2 019; 2 025

các số chia hết cho 9 là: 450; 2 025.

Lời giải:

Tổng các chữ số của số 290 là 2 + 9 + 0 =11 không chia hết cho 9 nên 290 không chia hết cho 9. Do đó mà cô không thể chia đều 290 học sinh đi dã ngoại thành 9 nhóm.

Vậy không thể chia đều số học sinh của khối 6 thành 9 nhóm.

Lời giải:

Tổng các chữ số của 162 là 1 + 6 + 2 = 9 chia hết cho 9 nên 162 chia hết cho 9. Do đó chia 162 em học sinh thành các đội, thì không có đội nào không đủ 9 học sinh.

a) Chia hết cho 2 

b) Chia hết cho 3

c) Chia hết cho 5 

d) Chia hết cho 9.

Lời giải:

Điều kiện $*\in \mathbb{N}\mathrm{,0}\le *\le 9$

a) Số $\overline{345*}$ chia hết cho 2 thì nó phải có tận cùng là chữ số chẵn nên $*\in \text{{}0;2;4;6;8\}$

Vậy có thể thay * bằng các chữ số: 0; 2; 4; 6; 8

b) Số $\overline{345*}$  chia hết cho 3 thì tổng các chữ số của nó cũng chia hết cho 3.

Do đó 3 + 4 + 5 + * = 12 + * chia hết cho 3.

Mà 12 chia hết cho 3 nên * cũng phải chia hết cho 3 nên $*\in \text{{}0;3;6;9\}$

Vậy có thể thay * bằng các chữ số: 0; 3; 6; 9

c) Số $\overline{345*}$ chia hết cho 5 thì nó phải có tận cùng là 0 hoặc 5 nên $*\in \text{{}0;5\}$

Vậy có thể thay * bằng các chữ số: 0 ; 5

d) Số  $\overline{345*}$ chia hết cho 9 thì tổng các chữ số của nó cũng chia hết cho 9

Do đó 3 + 4 + 5 + * = 12 + * chia hết cho 9 nên $*\in \text{{}6\}$

Vậy có thể thay * bằng chữ số 6.

a) Các số đó chia hết cho 2

b) Các số đó chia hết cho 5

Lời giải:

a) Vì số cần tìm là số tự nhiên chia hết cho 2 nên số cần tìm có chữ số tận cùng là 0 hoặc 4.

+) Với chữ số tận cùng là 0 và có ba chữ số khác nhau ta được số cần tìm là: 340; 430.

+) Với chữ số tận cùng là 4, chữ số 0 không thể đứng đầu nên số 0 ở hàng chục và số tự nhiên có ba chữ số khác nhau nên ta được số cần tìm là: 304

Vậy các số chia hết cho 2 là:  304; 340; 430.

b) Vì số cần tìm là số tự nhiên chia hết cho 5 nên số cần tìm có chữ số tận cùng là 0.

Vì số tự nhiên có ba chữ số khác nhau nên ta viết được các số: 340; 430

Vậy các số chia hết cho 5:  340; 430.

Bài 2.16 trang 37 Toán lớp 6 Tập 1: Từ các chữ số 5, 0, 4, 2 viết các số tự nhiên có ba chữ số khác nhau sao cho mỗi số đó chia hết cho 3.

Lời giải:

Ta thấy:

5 + 4 + 0 = 9

4 + 2 + 0 = 6

Bộ ba chữ số khác nhau có tổng của chúng chia hết cho 3 là: (5; 4; 0) và (4; 2; 0)

+) Với bộ ba chữ số (5; 4; 0) ta được các số tự nhiên có ba chữ số khác nhau là: 504; 540; 405; 450

+) Với bộ ba chữ số (2; 4; 0) ta được các số tự nhiên có ba chữ số khác nhau là: 420; 402; 240; 204.

Vậy các số cần tìm là: 504; 540; 405; 450; 420; 402; 240; 204.

Bài giảng Toán 6 Bài 9: Dấu hiệu chia hết - Kết nối tri thức