Giải Toán lớp 6 Kết nối tri thức Luyện tập chung trang 43
Hoidap.vietjack.com trân trọng giới thiệu: Lời giải bài tập Toán lớp 6 Luyện tập chung trang 43 sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 6 Luyện tập chung trang 43. Mời các bạn đón xem:
Giải bài tập Toán lớp 6 Luyện tập chung
Video giải Toán 6 Luyện tập chung - Kết nối tri thức
Bài 2.25 trang 43 Toán lớp 6 Tập 1:
Từ các số 5, 0, 1, 3, viết các số tự nhiên có ba chữ số khác nhau thỏa mãn điều kiện:
Lời giải:
a) Gọi số tự nhiên cần tìm có ba chữ số khác nhau là
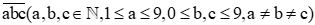
Vì số đó chia hết cho 5 nên chữ số tận cùng là 0 hoặc 5. Do đó c = 0 hoặc c = 5.
+) Với c = 0, ta có bảng chữ số a, b khác nhau và khác 0 thỏa mãn là:
|
a |
1 |
5 |
3 |
5 |
1 |
3 |
|
b |
5 |
1 |
5 |
3 |
3 |
1 |
Do đó ta thu được các số: 150; 510; 350; 530; 130; 310.
+) Với c = 5, a 0 nên a = 1 hoặc 3, ta có bảng chữ số a, b khác nhau thỏa mãn là:
|
a |
1 |
3 |
1 |
3 |
|
b |
0 |
0 |
3 |
1 |
Do đó ta thu được các số: 105; 305; 135; 315
Vậy các số tự nhiên có ba chữ số khac nhau chia hết cho 5 được viết từ các chữ số đã cho: 130; 135; 105; 150; 310; 315; 350; 305; 510; 530.
b) Gọi số tự nhiên cần tìm có ba chữ số khác nhau là
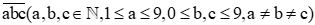
Vì số đó chia hết cho 3 nên tổng các chữ số của nó phải chia hết cho 3 hay (a + b + c) chia hết cho 3.
Ta thấy cặp 3 chữ số khác nhau có tổng chia hết cho 3 là: (5, 0, 1); (5, 1, 3) vì (5 + 0 + 1 = 6 chia hết cho 3 và 5 + 1 + 3 = 9 chia hết cho 3)
+) Với (5, 0, 1) ta có các số cần tìm là: 105; 150; 510; 501
+) Với (5, 1, 3) ta có các số cần tìm là: 135; 153; 351; 315; 513; 531
Vậy các số tự nhiên có ba chữ số khac nhau chia hết cho 3 được viết từ các chữ số đã cho: 135; 153; 351; 315; 513; 531; 105; 150; 510; 501.
Bài 2.26 trang 43 Toán lớp 6 Tập 1:
Hãy phân tích các số A, B ra thừa số nguyên tố:
Lời giải:
Bài 2.27 trang 43 Toán lớp 6 Tập 1:
Tìm số tự nhiên x không vượt quá 22 sao cho:
Lời giải:
a) 100 - x chia hết cho 4. Mà 100 chia hết cho 4 nên x chia hết cho 4
Do đó x là bội của 4
Ta có: B(4) = {0; 4; 8; 12; 16; 20; 24;…}
Vì x không vượt quá 22 nên x ∈ {0; 4; 8; 12; 16; 20}
Vậy x ∈ {0; 4; 8; 12; 16; 20}.
b) 18 + 90 + x chia hết cho 9. Mà 18 và 90 chia hết cho 9 nên x chia hết cho 9
Do đó x là bội của 9
Ta có: B(9) = {0; 9; 18; 27;…}
Vì x không vượt quá 22 nên x ∈ {0; 9; 18}
Vậy x ∈ {0; 9; 18}.
Lời giải:
Gọi số nhóm là x (nhóm, )
Vì cô giáo muốn chia lớp có 40 học sinh thành nhiều nhóm có số người như nhau nên
40 x hay Ư(40)
Ư(40) = {1; 2; 4; 5; 8; 10; 20; 40}
Ta có bảng sau:
| Số nhóm | 1 | 2 | 4 | 5 | 8 | 10 | 20 | 40 |
| Số người mỗi nhóm | 40 | 20 | 10 | 8 | 5 | 4 | 2 | 1 |
Vì mỗi nhóm có nhiều hơn 3 người nên mỗi nhóm có thể có 4 người; 5 người; 8 người; 10 người; 20 người hoặc 40 người.
Vậy mỗi nhóm có thể có 4 người; 5 người; 8 người; 10 người; 20 người hoặc 40 người.
Lời giải:
Các cặp số nguyên tố sinh đôi nhỏ hơn 40:
+) 3 và 5
+) 5 và 7
+) 11 và 13
+) 17 và 19
+) 29 và 31.
Bài viết liên quan
- Giải Toán lớp 6 Kết nối tri thức Bài 9: Dấu hiệu chia hết
- Giải Toán lớp 6 Kết nối tri thức Bài 10: Số nguyên tố
- Giải Toán lớp 6 Kết nối tri thức Bài 11: Ước chung - Ước chung lớn nhất
- Giải Toán lớp 6 Kết nối tri thức Bài 12: Bội chung - Bội chung nhỏ nhất
- Giải Toán lớp 6 Kết nối tri thức Luyện tập chung trang 54, 55
