Video Giải Toán 6 Luyện tập chung trang 54 - 55 - sách Kết nối tri thức - Cô Hoàng Thanh Xuân (Giáo viên VietJack)

Bài 2.45 trang 55 Toán lớp 6 Tập 1:

Cho bảng sau:

a) Tìm các số thích hợp thay vào ô trống trong bảng;

b) So sánh tích ƯCLN(a, b) . BCNN(a, b) và a.b.

Em rút ra kết luận gì?

Lời giải:

a) 

+) Ở cột thứ hai:

a = 34 = 2.17; b = 51 = 3.17

⇒ ƯCLN(a; b) = 17 ;  BCNN(a; b) = 2.3.17 = 102.

ƯCLN(a, b) . BCNN(a, b) = 17.102 = 1 734.

a.b = 34. 51 = 1 734.

+) Ở cột thứ ba:

a = 120 =2³.3.5 ;   b = 70 = 2.5.7

⇒ ƯCLN(a; b) = 2. 5 = 10 ;  BCNN(a; b) = 2³.3.5.7 = 840

ƯCLN(a, b) . BCNN(a, b) = 10. 840 = 8 400.

a.b = 120. 70 = 8 400.

+) Ở cột thứ tư:

a = 15 =3.5;   b = 28 = 2².7

⇒ ƯCLN(a; b) = 1 ;  BCNN(a; b) =  

ƯCLN(a, b) . BCNN(a, b) =1. 420 = 420.

a.b = 15. 28 = 420.

+) Ở cột thứ năm:

a = 2 987;   b = 1

⇒ ƯCLN(a; b) = 1 ;  BCNN(a; b) = 2 987

ƯCLN(a, b) . BCNN(a, b) = 1 . 2 987 = 2 987.

a.b = 2 987 . 1 = 2 987

Ta có bảng sau:

b) So sánh: ƯCLN(a, b) . BCNN(a, b) = a.b

Em rút ra kết luận: tích của BCNN cà ƯCLN của hai số tự nhiên bất kì bằng tích của chúng.

Bài 2.46 trang 55 Toán lớp 6 Tập 1:

Tìm ƯCLN và BCNN của:

a) 3.5² và 5².7

b) 2².3.5; 3².7 và 3.5.11

Lời giải:

a) 3.5² và 5².7

+) Ta thấy các thừa số nguyên tố chung là 5 và thừa số nguyên tố riêng là 3 và 7

+) Số mũ nhỏ nhất của 5 là 2 nên ƯCLN cần tìm là 5² = 25

+) Số mũ lớn nhất của 3 là 1, số mũ lớn nhất của 5 là 2, số mũ lớn nhất của 7 là 1 nên BCNN cần tìm là 3.5².7 = 525

Vậy ƯCLN cần tìm là 5² = 25

        BCNN cần tìm là 3.5².7  = 525.

b) 2².3.5; 3².7  và 3.5.11

+) Ta thấy các thừa số nguyên tố chung là 3 và thừa số nguyên tố riêng là 2; 5; 7; 11

+) Số mũ nhỏ nhất của 3 là 1 nên ƯCLN cần tìm là 3

+) Số mũ lớn nhất của 2 là 2, số mũ lớn nhất của 3 là 2, số mũ lớn nhất của 5 là 1, số mũ lớn nhất của 7 là 1, số mũ lớn nhất của 11 là 1 nên BCNN cần tìm là 2².3².5.7.11 = 13 860

Vậy 

ƯCLN cần tìm là 3 

BCNN cần tìm là 2².3².5.7.11 = 13 860.

Bài 2.47 trang 55 Toán lớp 6 Tập 1:

Các phân số sau đã tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản.

a) 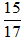                b) .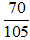

Lời giải:

a) Vì ƯCLN(15, 17) = 1 nên phân số 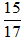 là phân số tối giản.

b) Ta có: 70 = 2.7.5;    105= 3.5.7

+) Thừa số nguyên tố chung là 5 và 7

+ Số mũ nhỏ nhất của 5 là 1, số mũ nhỏ nhất của 7 là 1 nên ƯCLN(70, 105) = 35. 

Do đó 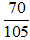 không là phân số tối giản

Ta có: 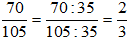. Ta được  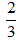là phân số tối giản vì ƯCLN(2, 3) = 1.

Bài 2.48 trang 55 Toán lớp 6 Tập 1: Hai vận động viên chạy xung quanh một sân vận động. Hai vận động viên xuất phát tại cùng một thời điểm, cùng vị trí và chạy cùng chiều. Vận động viên thứ nhất chạy một vòng sân hết 360 giây, vận động viên thứ hai chạy một vòng sân mất 420 giây. Hỏi sau bao nhiêu phút họ lại gặp nhau, biết tốc độ di chuyển của họ không đổi?

Lời giải:

Đổi 360 giây = 6 phút, 420 giây = 7 phút

Giả sử sau x phút họ lại gặp nhau.

Vận động viên thứ nhất chạy một vòng sân hết 6 phút nên x là bội của 6.

Vận động viên thứ hai chạy một vòng sân hết 7 phút nên x là bội của 7.

Suy ra x ∈ BC(6; 7).

Mà x ít nhất nên x = BCNN(6; 7).

6 = 2.3;   7 = 7

  x = BCNN(6; 7) = 2.3.7 = 42

Vậy sau 42 phút họ lại gặp nhau.

Bài 2.49 trang 55 Toán lớp 6 Tập 1:

Quy đồng mẫu các phân số sau:

a)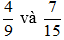

b)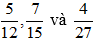

Lời giải:

a) Ta có: 9 =3²;   15 =3.5 nên BCNN(9, 15) = 3².5 = 45. Do đó ta có thể chọn mẫu chung là 45.

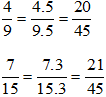
b) Ta có: 12 =2².3;   15 = 3.5 ; 27 = 3³ nên BCNN(12, 15, 27) = 2².3³.5 = 540. Do đó ta có thể chọn mẫu chung là 540.

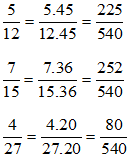
Bài 2.50 trang 55 Toán lớp 6 Tập 1: Từ ba tấm gỗ có độ dài 56 dm, 48 dm và 40 dm, bác thợ mộc muốn cắt thành các thanh gỗ có độ dài như nhau mà không để thừa mẩu gỗ nào. Hỏi bác cắt như thế nào để được các thanh gỗ có độ dài lớn nhất có thể?

Lời giải:

Các thanh gỗ có độ dài lớn nhất được cắt ra là ƯCLN(56, 48, 40)

Ta có:  56 = 2³.7   ;    48 = 2⁴3  ;   40 = 2³.5

Ta thấy thừa số nguyên tố chung là 2 và có số mũ nhỏ nhất là 3

Do đó ƯCLN(56, 48, 40) = 2³ = 8

Vậy chiều dài các thanh gỗ lớn nhất có thể cắt là 8 dm.

Bài 2.51 trang 55 Toán lớp 6 Tập 1: Học sinh lớp 6A khi xếp thành hàng 2, hàng 3, hàng 7 đều vừa đủ hàng. Hỏi số học sinh lớp 6A là bao nhiêu, biết rằng số học sinh nhỏ hơn 45.

Lời giải:

Học sinh lớp 6A khi xếp thành hàng 2, hàng 3, hàng 7 đều vừa đủ hàng.

Do đó số học sinh lớp 6A là BC(2, 3, 7)

BCNN(2, 3, 7) = 2.3.7 = 42 nên BC(2, 3, 7) = B(42) = {0; 42; 84, ...}

Mà số học sinh nhỏ hơn 45 nên số học sinh lớp 6A là 42.

Vậy số học sinh lớp 6A là 42 học sinh.

Bài 2.52 trang 55 Toán lớp 6 Tập 1:

Hai số có BCNN là 2³.3.5³ và ƯCLN là 2².5. Biết một trong hai số bằng 2².3.5, tìm số còn lại.

Lời giải:

Gọi số cần tìm là x.

Tích của hai số đã cho là (2².3.5).x

Tích của BCNN và ƯCLN của hai số đã cho là: 

( 2².3.5).(2².5) = (2³.2²).3.(5³.5) =2⁵.3.5⁴

Theo Bài tập 2.45, ta có tích của BCNN và ƯCLN của hai số tự nhiên bất kì thì bằng tích của hai số đó.

Do đó: ( 2².3.5). x = 2⁵.3.5⁴ 

                       x = (2⁵.3.5⁴) : (2².3.5)

                       x = (2⁵ : 2²).(3:3).(5⁴ : 5)

                        x = (2^5-2).1.5^4-1

                       x = 2³.5³

Vậy số cần tìm là 2³.5³.