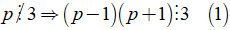Toán lớp 6 Bài 14: Số nguyên tố. Hợp số. Bảng số nguyên tố
Lý thuyết tổng hợp Toán học lớp 6 Bài 14: Số nguyên tố. Hợp số. Bảng số nguyên tố chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 6. Hy vọng bộ tổng hợp lý thuyết Toán lớp 6 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 6.
Bài 14: Số nguyên tố. Hợp số. Bảng số nguyên tố
A. Lý thuyết
1. Số nguyên tố. Hợp số
Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.
Ví dụ:
+ U(11) = {11; 1} nên 11 là số nguyên tố.
+ Số 15 có 4 ước là 1; 3; 5; 15 nên 15 là hợp số.
Chú ý:
• Số 0 và số 1 không là số nguyên tố và cũng không là hợp số.
• Các số nguyên tố nhỏ hơn 10 là 2; 3; 5; 7.
2. Lập bảng các số nguyên tố nhỏ hơn 100
Số nguyên tố là các số trong khung màu xanh
Nhận xét: Số nguyên tố nhỏ nhất là số 2, đó là số nguyên tố chẵn duy nhất.

3. Bài tập tự luyện
Câu 1: Chứng minh rằng mọi số nguyên tố lớn hơn 2 đều có dạng là 4n ± 1
Hướng dẫn giải:
Khi chia một số tự nhiên a lớn hơn 2 cho 4 thì ta được các số dư là 0, 1, 2, 3. Trường hợp các số dư là 0 và 2 thì a là hợp số. Ta xét chỉ xét trường hợp số dư là 1 và 3.
+ Với mọi trường hợp số dư là 1 ta có a = 4n + 1
+ Với mọi trường hợp số dư là 3 ta có a = 4n + 3 = 4n + 4 - 1 = 4(n + 1) - 1 = 4m - 1
Câu 2: Chứng minh rằng nếu p là số nguyên tố lớn hơn 3 thì (p - 1)(p + 1) chia hết cho 24.
Hướng dẫn giải:
Ta có tích ba số tự nhiên liên tiếp chia hết cho 3:(p - 1)p(p + 1) ⋮ 3 mà p là số nguyên tố lớn hơn 3 nên
Mặt khác p là số nguyên tố lớn hơn 3 nên p là số lẻ, p - 1 và p + 1 là hai số chẵn liên tiếp có một số là bội của 4 nên tích của chúng chia hết cho 8 (2)
Từ (1), (2) suy ra (p - 1)(p + 1) chia hết cho hai số nguyên tố cùng nhau là 3 và 8
Vậy (p - 1)(p + 1) chia hết cho 24.
B. Bài tập trắc nghiệm
Câu 1: Khẳng định nào sau đây sai?
A. 0 và 1 không phải là số nguyên tố cũng không phải là hợp số.
B. Cho số a > 1, a có 2 ước thì a là hợp số.
C. 2 là số nguyên tố chẵn duy nhất.
D. Số nguyên tố là số tự nhiên lớn hơn 1 mà chỉ có hai ước 1 và chính nó.
Đáp án
Số a phải là số tự nhiên lớn hơn 1 và có nhiều hơn 2 ước thì a mới là hợp số
Nên đáp án B sai.
Chọn đáp án B.
Câu 2: Khẳng định nào sau đây đúng?
A. A = {0; 1} là tập hợp số nguyên tố
B. A = {3; 5} là tập hợp số nguyên tố.
C. A = {1; 3; 5} là tập hợp các hợp số.
D. A = {7; 8} là tập hợp các hợp số.
Đáp án
+ Đáp án A sai vì 0 và 1 không phải là số nguyên tố.
+ Đáp án B đúng vì 3 và 5 là số nguyên tố.
+ Đáp án C sai vì 1 không phải là hợp số và 3, 5 là số nguyên tố.
+ Đáp án D sai và 7 là số nguyên tố, 8 là hợp số.
Chọn đáp án B.
Câu 3: Kết quả của phép tính nào sau đây là số nguyên tố
A. 15 - 5 + 3 B. 7.2 + 1 C. 14.6:4 D. 6.4 - 12.2
Đáp án
Ta có
+ Đáp án A: 15 - 5 + 3 = 13 là số nguyên tố.
+ Đáp án B: 7.2 + 1 = 15 là hợp số.
+ Đáp án C: 14.6:4 = 84:4 = 21 là hợp số.
+ Đáp án D: 6.4 - 12.2 = 24 - 24 = 0 không phải là số nguyên tố, cũng không phải là hợp số
Chọn đáp án A.
Câu 4: Tìm số tự nhiên x để được số nguyên tố 3x¯
A. 7 B. 4 C. 6 D. 9
Đáp án
+ Đáp án A: 37 là số nguyên tố
+ Đáp án B: 34 không phải là số nguyên tố vì 34 chia hết cho {1; 2; 17; 34}
+ Đáp án C: 36 không phải là số nguyên tố vì 36 chia hết cho {1; 2; 3; ...; 36}
+ Đáp án D: 39 không phải là số nguyên tố vì 39 chia hết cho {1; 3; 13; 39}
Chọn đáp án A.
Câu 5: Cho các số 21; 71; 77; 101. Chọn phát biểu đúng trong các phát biểu sau?
A. Số 21 là hợp số, các số còn lại là số nguyên tố.
B. Có hai số nguyên tố và hai số là hợp số trong các số trên.
C. Chỉ có một số nguyên tố, còn lại là hợp số.
D. Không có số nguyên tố nào trong các số trên
Đáp án
+ Số 21 có các ước là 1; 3; 7; 21 nên 21 là hợp số.
+ Số 71 có các ước là 1; 71 nên 71 là số nguyên tố.
+ Số 77 có các ước là 1; 7; 11; 77 nên 77 là hợp số.
+ Số 101 chỉ có hai ước là 1; 101 nên 101 là số nguyên tố.
Chọn đáp án B.
Câu 6: Trong các khẳng định sau, khẳng định nào sai?
A. Có hai số tự nhiên liên tiếp đều là số nguyên tố
B. Mọi số nguyên tố đều là số lẻ
C. Có ba số lẻ liên tiếp đều là số nguyên tố
D. Số 1 không là số nguyên tố
Đáp án
Có hai số tự nhiên liên tiếp là 2 và 3 đều là số nguyên tố nên A đúng
Có ba số lẻ liên tiếp là 3; 5 và 7 đều là số nguyên tố nên C đúng
Số 1 không là số nguyên tố và cũng không là hợp số nên D đúng
Số 2 là số nguyên tố chẵn do đó B sai
Chọn đáp án B
Câu 7: Có bao nhiêu số nguyên tố có hai chữ số mà chữ số hàng đơn vị là 7
A. 5
B. 6
C. 7
D. 8
Đáp án
Số tự nhiên có hai chữ số với chữ số hàng đơn vị là 7 là: 17; 27; 37; 47; 57; 67; 77; 87; 97
Trong đó, số nguyên tố là: 17; 37; 47; 67; 97
Chọn đáp án A
Câu 8: Thay chữ số vào dấu * để 6*¯ là số nguyên tố
A. 5
B. 6
C. 7
D. 8
Đáp án
A: Ta được số 65. U(65) = {1; 5; 13; 65} nên 65 là hợp số
B: Ta được số 66. U(66) = {1; 2; 3;...; 66} nên 66 là hợp số
C: Ta được số 67. Ư(67) = {1; 67} nên 67 là số nguyên tố
Chọn đáp án C
Câu 9: Số tự nhiên có 2 chữ số khác nhau nhỏ nhất chia hết cho các số nguyên tố nhỏ hơn hoặc bằng 5 là:
A. 20
B. 25
C. 30
D. 35
Đáp án
Các số nguyên tố nhỏ hơn hoặc bằng 5 là: 2; 3; 5
Vì số cần tìm chia hết cho 2 và 5 nên có dạng a0¯
Vì a0¯ ⋮ 3 ⇒ a ⋮ ⇒ a ∈ {3; 6; 9}
Vì a0¯ là số nhỏ nhất nên a = 3
Vậy số cần tìm là 30
Chọn đáp án C
Câu 10: Viết tập hợp các số là hợp số trong các số sau: 1431; 635; 119; 73
A. {73}
B. {1431; 635; 119
C. {73; 119}
D. {73; 635}
Đáp án
Ta có các số 1431; 635; 119 là hợp số vì ngoài 1 và chính nó thì
1431 còn có ước là 3
635 còn có ước là 5
119 còn có ước là 7
Chọn đáp án B