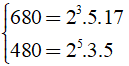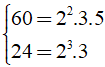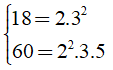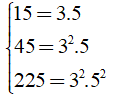Bài 17: Ước chung lớn nhất

A. Lý thuyết

1. Định nghĩa: Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.

2. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tố

   Bước 1: Phân tích mỗi số ra thừa số nguyên tố

   Bước 2: Chọn ra các thừa số nguyên tố chung.

   Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm

Ví dụ: Tìm ƯCLN (54;90)

   + Phân tích các số ra thừa số nguyên tố

54 = 2.3³

90 = 2.3².5

Thừa số nguyên tố chung là 2 và 3. Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 3 là 2

Vậy ƯCLN (54;90) = 2.3² = 18

Chú ý:

   + Nếu các số đã cho không có thừa số nguyên tố chung thì ƯCLN của chúng bằng 1.

   + Hai hay nhiều số có ƯCLN bằng 1 gọi là các số nguyên tố cùng nhau.

   + Trong các số đã cho, nếu số nhỏ nhất là ước của các số còn lại thì ƯCLN của các số đã cho chính là số nhỏ nhất ấy.

3. Cách tìm ước chung thông qua tìm ƯCLN

Để tìm ước chung của các số đã cho, ta có thể tìm các ước của ƯCLN của các số đó.

Ví dụ: Tìm các ước chung của 54 và 90

Ta đã chỉ ra ở ví dụ trên ƯCLN (54; 90) = 18

Các ước của 18 là: 1; 2; 3; 6; 9; 18.

Vậy ƯC (54; 90) = {1; 2; 3; 6; 9; 18}

4. Bài tập tự luyện

Câu 1: Một căn phòng hình chữ nhật có chiều dài là 680cm và chiều rộng là 480cm. Người ta muốn lát kín căn phòng đó bằng gạch hình vuông mà không có viên gạch nào bị cắt xén. Hỏi viên gạch đó có độ dài lớn nhất bằng bao nhiêu?

Hướng dẫn giải:

Ta có:

Gọi độ dài của viên gạch hình vuông là x.

Để lát kín căn phòng mà không có viên gạch nào bị cắt xén thì x phải là ước chung của chiều dài và chiều rộng.

Hay 680 ⋮ x và 480 ⋮ x ⇒ x ∈ ƯC(680; 480)

Để x lớn nhất thì ⇒ x = ƯCLN(680; 480)

Ta có: 

⇒ x = ƯCLN(680; 480) = 2³.5 = 40

Vậy để lát kín căn phòng đó mà không có viên gạch nào bị cắt xén thì độ dài lớn nhất của viên gạch là 40cm

Câu 2: Một khu đất hình chữ nhật có chiều dài là 60cm, chiều rộng là 24cm. Người ta chia thành những thửa đất hình vuông bằng nhau, để mỗi thửa đất có diện tích lớn nhất thì độ dài mỗi cạnh của thửa đất đó bằng?

Hướng dẫn giải:

Gọi độ dài cạnh của mỗi thửa đất hình vuông là x (cm)

Để diện tích của một thửa đất đó lớn nhất thì độ dài x lớn nhất.

Vì các thửa đất đó được chia ra từ khu đất hình chữ nhật có chiều dài là 60cm, chiều rộng là 24cm

Nên x phải là ước của 60 và 24 hay x ∈ ƯC(24; 60)

Khi đó x lớn nhất thì x = ƯCLN(24; 60)

Ta có: 

⇒ ƯCL(24; 60) = 2².3 = 12

Vậy mỗi thừa đất hình vuông có độ dài cạnh lớn nhất là 12cm

B. Bài tập trắc nghiệm

Câu 1: Tìm ƯCLN ( 16; 32; 112)?

A. 4     B. 8     C. 16     D. 32

Đáp án

Câu 2: Tìm ƯCLN(18; 60)?

A. 6     B. 30     C. 12     D. 18

Đáp án

Câu 3: ƯCLN của a và b là:

A. Bằng b nếu a chia hết cho b.

B. Bằng a nếu a chia hết cho b.

C. Là ước chung nhỏ nhất của a và b

D. Là hiệu của 2 số a và b.

Đáp án

Câu 4: Tìm ƯCLN của 15, 45 và 225

A. 18     B. 3     C. 15     D. 5

Đáp án

Câu 5: Cho a = 3².5.7 và b = 2⁴.3.7. Tìm ƯCLN của a và b

A. ƯCLN(a; b) = 3.7     B. ƯCLN(a; b) = 3².7²

C. ƯCLN(a; b) = 2⁴.5     D. ƯCLN(a; b) = 2⁴.3².5.7

Đáp án

Câu 6: Số tự nhiên a lớn nhất thỏa mãn 90 ⋮ a và 135 ⋮ a là:

A. 15

B. 30

C. 45

D. 60

Đáp án

Câu 7: Một đội ý tế có 36 bác sĩ và 108 y tá. Có thể chia đội y tế đó nhiều nhất thành mấy tổ để các bác sĩ cũng như các y tá được chia đều vào mỗi tổ?

A. 36

B. 18

C. 9

D. 6

Đáp án

Câu 8: Trong hai số sau, hai số nào là hai số nguyên tố cùng nhau:

A. 2 và 6

B. 3 và 10

C. 6 và 9

D. 15 và 33

Đáp án

Câu 9: Tìm số tự nhiên x, biết rằng 162 ⋮ x; 360 ⋮ x và 10 < x < 20 :

A. x = 6

B. x = 9

C. x = 18

D. x = 36

Đáp án

Câu 10: Lớp 9A có 45 học sinh, lớp 9B có 42 học sinh, lớp 9C có 48 học sinh. Trong ngày khai giảng, ba lớp cùng xếp thành một số hàng dọc như nhau để diễu hành mà không lớp nào có người lẻ hàng. Số hàng dọc nhiều nhất có thể xếp được là:

A. 2

B. 3

C. 4

D. 5

Đáp án