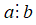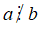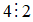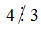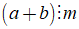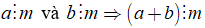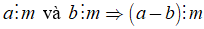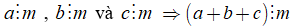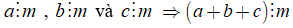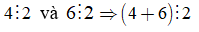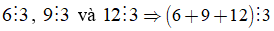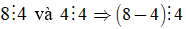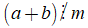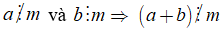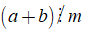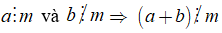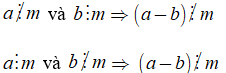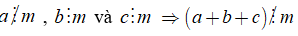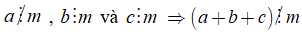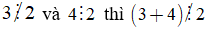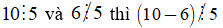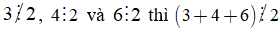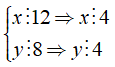Toán lớp Bài 10: Tính chất chia hết của một tổng
Lý thuyết tổng hợp Toán học lớp 6 Bài 10: Tính chất chia hết của một tổng chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 6. Hy vọng bộ tổng hợp lý thuyết Toán lớp 6 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 6.
Bài 10: Tính chất chia hết của một tổng
A. Lý thuyết
1. Nhắc về quan hệ chia hết
Số tự nhiên a chia hết cho số tự nhiên b khác 0 nếu có số tự nhiên k sao cho a = b.k
+ Kí hiệu a chia hết cho b là
+ Kí hiệu a không chia hết cho b là
Ví dụ:
+ 4 chia hết cho 2, kí hiệu là:
+ 4 không chia hết cho 3, kí hiệu là:
2. Tính chất 1
Nếu 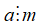
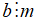
+ Kí hiệu "⇒" được đọc là suy ra hoặc kéo theo.
+ Ta có thể viết 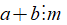
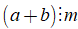
Chú ý:
• Tính chất 1 cũng đúng đối với một hiệu
• Tính chất 1 cũng đúng với một tổng nhiều số hạng
Tổng quát: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
Ví dụ:
+ Ta có:
+ Ta có:
+ Ta có:
3. Tính chất 2
Nếu 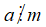
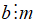
Nếu 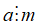
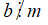
+ Kí hiệu "⇒" được đọc là suy ra hoặc kéo theo.
+ Ta có thể viết 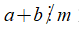
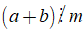
Chú ý:
• Tính chất 2 cũng đúng đối với một hiệu
• Tính chất 2 cũng đúng với một tổng nhiều số hạng, trong đó chỉ có một số hạng không chia hết cho m, các số hạng còn lại đều chia hết cho m:
Tổng quát: Nếu chỉ có một số hạng của tổng không chia hết cho một số , còn các số hạng còn lại đều chia hết cho số đó thì tổng đó không chia hết cho số đó.
Ví dụ:
+ Ta có:
+ Ta có:
+ Ta có:

4. Bài tập tự luyện
Câu 1: Cho ba số tự nhiên a, b, c trong đó a và b là các số chia cho 5 dư 3 còn c là số chia cho 5 dư 2. Chứng minh rằng mỗi tổng hoặc hiệu: a + c; a - b chia hết cho 5
Hướng dẫn giải:
Theo bài ra ta có: a chia cho 5 dư 3 nên a có dạng: a = 5q + 3 (q ∈ N)
Tương tự b chia cho 5 dư 3 nên b có dạng: b = 5p + 3 (p ∈ N)
c chia cho 5 dư 2 nên c có dạng: c = 5m + 2 (m ∈ N)
Xét a + c = (5q + 3) + (5m + 2)
⇔ a + c = 5(q + m) + (3 + 2)
⇔ a + c = 5(q + m) + 5
Ta thấy 5(q + m) ⋮ 5 và 5 ⋮ 5 nên a + c chia hết cho 5.
Tương tự ta có: a - b = (5q + 3) - (5p + 3)
⇔ a - b = 5 (q - p)
Ta thấy 5(q - p) ⋮ 5 nên a - b chia hết cho 5.
Câu 2: Tìm số tự nhiên x sao cho 215 + x chia hết cho 11.
Hướng dẫn giải:
Ta có: 215 chia cho 11 được thương là 19 dư 6 nên 215 = 19.11 + 6
Khi đó ta có: 215 + x = 11.19 + 6 + x
Có 19.11 chia hết cho 11 nên 215 + x chia hết cho 11 khi 6 + x chia hết cho 11.
Suy ra x là số chia cho 11 dư 5 nên x có dạng là x = 11q + 5 (q ∈ N)
Vậy x cần tìm có dạng là x = 11q + 5 (q ∈ N) thì 215 + x chia hết cho 11.
B. Bài tập trắc nghiệm
Câu 1: Nếu a không chia hết cho 2 và b chia hết cho 2 thì tổng a + b
A. Chia hết cho 2
B. Không chia hết cho 2
C. Có tận cùng là chữ số 2.
D. Có tận cùng là 1; 3; 5; 7; 9
Đáp ánTheo tính chất 2: Nếu a không chia hết cho 2 và b chia hết cho 2 thì a + b không chia hết cho 2
Chọn đáp án B.
Câu 2: Tổng nào sau đây chia hết cho 7
A. 49 + 70 B. 14 + 51 C. 7 + 134 D. 10 + 16
Đáp ánTheo tính chất 1: Ta có 49 chia hết cho 7 và 70 chia hết cho 7 nên 49 + 70 chia hết cho 7.
Chọn đáp án A.
Câu 3: Nếu x ⋮ 2 và y ⋮ 4 thì tổng x + y chia hết cho?
A. 2 B. 4 C. 8 D. Không xác định
Đáp ánTa có: y ⋮ 4 ⇒ y ⋮ 2
x ⋮ 2 và y ⋮ 2 ⇒ (x + y) ⋮ 2
Chọn đáp án A.
Câu 4: Nếu x ⋮ 12 và y ⋮ 8 thì x - y chia hết cho
A. 6 B. 3 C. 4 D. 12
Đáp ánTa có
Vì x ⋮ 4; y x ⋮ 4 ⇒ (x - y) x ⋮ 4
Chọn đáp án C.
Câu 5: Chọn câu sai
A. 49 + 105 + 399 chia hết cho 7
B. 84 + 48 + 120 không chia hết cho 8
C. 18 + 54 + 12 chia hết cho 9
D. 18 + 54 + 15 không chia hết cho 9
Đáp ánTa có: 18 ⋮ 9; 54 ⋮ 9; 12 không chia hết 9 ⇒ (18 + 54 + 12) không chia hết 9
Đáp án C sai.
Chọn đáp án C.
Câu 6: Có tổng M = 75 + 120 + x. Với giá trị nào của x dưới dây thì M ⋮ 3?
A. x = 7 B. x = 5 C. x = 4 D. x = 12
Đáp ánTa có: 75 ⋮ 3; 120 ⋮ 3. Vậy để M ⋮ 3 thì x ⋮ 3
Trong bốn đáp án ta thấy chỉ có x = 12 thỏa mãn điều kiện
Do đó giá trị cần tìm là x = 12
Chọn đáp án D.
Câu 7: Tìm số tự nhiên x để A = 75 + 1003 + x chia hết cho 5
A. x ⋮ 5 B. x chia cho 5 dư 1
C. x chia cho 5 dư 2 D. x chia cho 5 dư 3
Đáp ánTa thấy 75 chia hết cho 5 và 1003 không chia hết cho 5
Nên để A = 75 + 1003 + x chia hết cho 5 thì (1003 + x) chia hết cho 5
Mà 1003 chia cho 5 dư 3 nên để (1003 + x) chia hết cho 5 thì x chia cho 5 dư 2
Chọn đáp án C.
Câu 8: Cho A = 12 + 15 + 36 + x, x ∈ ℕ. Tìm điều kiện của x để A không chia hết cho 9.
A. x chia hết cho 9 B. x không chia hết cho 9
C. x chia hết cho 4 D. x chia hết cho 3
Đáp ánTa có: A = (12 + 15) + 36 + x
Vì 12 + 15 = 27 ⋮ 9; 36 ⋮ 9 ⇒ (12 + 15 + 36) ⋮ 9
Do đó để A không chia hết cho 9 thì x không chia hết cho 9
Chọn đáp án B.
Câu 9: Trong các khẳng định sau, khẳng định nào sai?
A. Nếu mỗi số hạng của tổng chia hết cho 7 thì tổng chia hết cho 7.
B. Nếu mỗi số hạng không chia hết cho 7 thì tổng không chia hết cho 7.
C. Nếu tổng của hai số chia hết cho 5 và một trong hai số đó chia hết cho 5 thì số còn lại chia hết cho 5.
D. Nếu hiệu của hai số chia hết cho 5 và một trong hai số đó chia hết cho 5 thì số còn lại chia hết cho 5.
Đáp ánDựa vào các tính chất chia hết ta thấy đáp án A, C, D đúng
Đáp án B sai. Ví dụ:
Ta có: 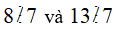
Chọn đáp án B
Câu 10: Khi chia số tự nhiên a cho 12, ta được số dư là 8. Khẳng định nào sau đây đúng?
A. a chia hết cho 6
B. a chia hết cho 4
C. a chia hết cho 3
D. Cả A, B, C đều đúng
Đáp ánSố tự nhiên a chia cho 12 được số dư là 8 nên a = 12k + 8, k ∈ ℕ
Ta có: 12k ⋮ 4; 8 ⋮ 4 ⇒ 12k + 8 ⋮ 4
Chọn đáp án B