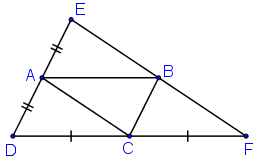
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua C. Chứng minh rằng E đối xứng với điểm F qua điểm B.
Quảng cáo
1 câu trả lời 756
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.
+ E đối xứng với D qua A
⇒ AE = AD
Mà BC = AD
⇒ BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE)
⇒ AEBC là hình bình hành
⇒ EB //= AC (1).
+ F đối xứng với D qua C
⇒ CF = CD
Mà AB = CD
⇒ AB = CF
Mà AB // CF (vì AB // CD ≡ CF)
⇒ ABFC là hình bình hành
⇒ AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
⇒ B là trung điểm EF
⇒ E đối xứng với F qua B
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
9908
Đã trả lời bởi chuyên gia
9908 -
 Đã trả lời bởi chuyên gia
7703
Đã trả lời bởi chuyên gia
7703
Gửi báo cáo thành công!