cho hình thang cân ABCD(AB//CD)có 2 đường chéo vuông góc với nhau.Chứng minh chiều cao của hình thang cân bằng nửa tổng độ dài của 2 cạnh đáy
Quảng cáo
2 câu trả lời 3955
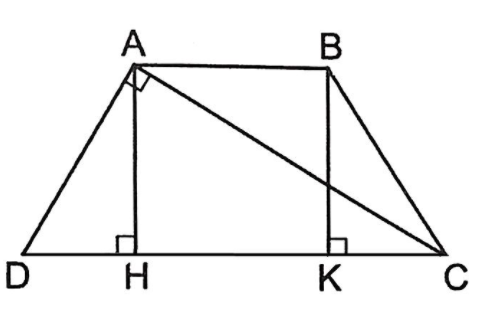

Ta có : ( đối đỉnh )
⇒ ΔAEF= ΔDEH ( ch - gn )
→
→ ΔAHC vuông cân tại HH
→ AH = HC
→ AB + DB = 2 × AH
→ (AB + DB ):2 = AH
Vậy chiều cao của hình thang cân bằng nửa tổng độ dài của 2 cạnh đáy
kẻ AE//BD, AE giao CD = E
=> AE = BD
=> AB= ED
ABCD là hình thang cân
=> AC= BD ( t/c hình thang )
mà AE= BD ( cmt )
=> AE= AC
=> tg AEC cân tại A
AH là đường cao đồng thời là đường trung tuyến
=> HE=HC
Gọi AC giao BD tại O
AE// BD ( gt )
=> góc EAC = góc DOC = 90 độ ( đồng vị )
tam giac AEC vuông cân
=> AH = EC/ 2 ( vì trong tam giac vuông cân đường trung tuyến bằng nửa cạnh huyền )
=> 2AH = EC
mà EC = ED + DC
ED = AB ( cmt )
=> AB+DC = 2AH đpcm

Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
9895
Đã trả lời bởi chuyên gia
9895 -
 Đã trả lời bởi chuyên gia
7691
Đã trả lời bởi chuyên gia
7691


