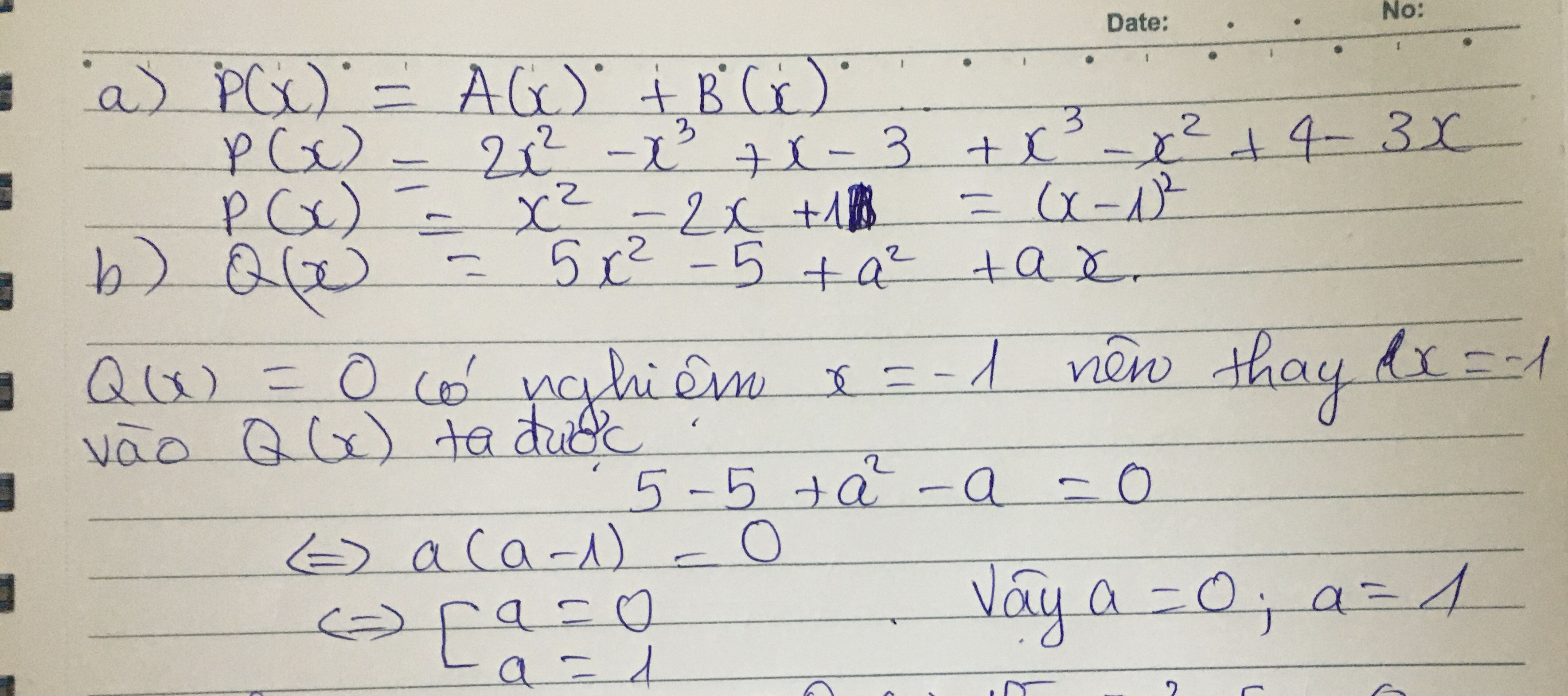Cho hai đa thức A(x) = 2x2 – x3 + x – 3 và B(x) = x3 – x2 + 4

Bình Phạm

đã hỏi trong Lớp 7 Toán học

· 16:23 30/07/2021

Câu hỏi trắc nghiệm Toán 7 có đáp án

Cho hai đa thức A(x) = 2x2 – x3 + x – 3 và B(x) = x3 – x2 + 4 – 3x.

Tính P(x) = A(x) + B(x).

b) Cho đa thức Q(x) = 5x2 – 5 + a2 + ax. Tìm các giá trị của a để Q(x) có nghiệm x = – 1.

Trả Lời

Hỏi chi tiết

Trả lời trong APP VIETJACK

Quảng cáo

3 câu trả lời 6794

Hằng

3 năm trước

$\begin{array}{l} A(x) = 2{x^2} - {x^3} + x - 3\\ B(x) = {x^3} - {x^2} + 4 - 3x\\ a)P\left( x \right){\rm{ }} = {\rm{ }}A\left( x \right){\rm{ }} + {\rm{ }}B\left( x \right)\\ = (2{x^2} - {x^3} + x - 3) + ({x^3} - {x^2} + 4 - 3x)\\ = 2{x^2} - {x^3} + x - 3 + {x^3} - {x^2} + 4 - 3x\\ = {x^2} - 2x + 1 \end{array}$

$b)Q\left( x \right) = 5{x^2}-5 + {a^2} + ax$

để Q(x) có nghiệm x = – 1. thì

$\begin{array}{l} Q( - 1) = 0\\ = > 5{( - 1)^2} - 5 + {a^2} + a.( - 1) = 0\\ = > {a^2} - a = 0\\ = > a(a - 1) = 0\\ = > \left[ \begin{array}{l} a = 0\\ a - 1 = 0 \end{array} \right.\\ = > \left[ \begin{array}{l} a = 0\\ a = 1 \end{array} \right. \end{array}$

(+1) 0 bình luận

Đăng nhập để hỏi chi tiết

HẰNG NGA

3 năm trước

0 bình luận

Đăng nhập để hỏi chi tiết

Như Huynh Nguyễn

2 năm trước

a=1 , a=0

0 bình luận

Đăng nhập để hỏi chi tiết

Quảng cáo

3 câu trả lời 6794

Câu hỏi hot cùng chủ đề

Bài viết mới nhất Lớp 7